Математическая обработка теодолитного хода

Математическая обработка состоит из: увязки (уравнивания) измеренных углов; вычисления дирекционных углов (азимутов) и румбов; вычисления горизонтальных проложений линий; определения приращений координат и их уравнивания и вычисления координат пунктов теодолитного хода.

Рассмотрим математическую обработку измерений на примере замкнутого теодолитного хода.

Результаты полевых измерений и вычислений записывают в ведомость вычисления координат (табл. 7.1).

1) Выполняется оценка качества результатов измерения углов, которая состоит из:

– вычисления суммы измеренных углов ( );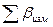

– определения теоретической суммы углов по формуле 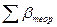_.= = 180˚(n – 2), где n – число углов в ходе;

– вычисления фактической угловой невязки по формуле ;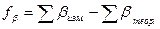

– определения величины допустимой угловой невязки согласно формуле f_{β доп.} = ± 0,8¢√n (для учебных целей допускается –1,5¢√n), где n – число углов.

Вычисленная угловая невязка не должна быть больше допустимой.

Фактическая невязка распределяется с обратным знаком в виде поправок в измеренные значения углов. Бо́льшие поправки необходимо вводить в углы с короткими сторонами. Сумма поправок должна равняться невязке с обратным знаком. Исправленные значения углов получают прибавлением поправок к измеренным углам. Контролем уравнивания служит получение теоретической суммы углов хода.

2) Вычисление дирекционных углов и румбов сторон теодолитного хода. Исходный дирекционный угол a_1-2 , получают в результате привязки стороны хода 1–2 к пунктам опорной геодезической сети или определяют для этой стороны хода магнитный азимут. По известному дирекционному углу a_1-2 и по исправленным углам β вычисляют дирекционные углы всех сторон хода. Если измерены правые по ходу углы, то вычисления выполняются по формуле 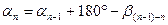, т. е. дирекционный угол последующего направления a_n равен дирекционному углу предыдущего направления a_n-1 плюс 180˚ и минус исправленный правый по ходу угол между этими направлениями β_(п-1)-п. Контролем вычислений дирекционных углов является получение исходного дирекционного угла. По дирекционным углам вычисляют румбы, пользуясь их зависимостью между собой (см. табл. 2.4).

3) Вычисление горизонтальных проложений производится для линий, имеющих наклон более 1,5˚ по формуле 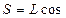v.

4) Вычисление приращений координат и их уравнивание. Приращения координат Δх и Δу находят по известным формулам прямой геодезической задачи: 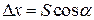; 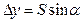, где S – горизонтальное проложение линии, a – дирекционный угол.

В замкнутом полигоне алгебраические суммы приращений координат должны равняться нулю: 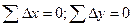. Но вследствии погрешностей S и a эти суммы отличаются от нуля, образуя линейные невязки приращений координат f_х и f_у , т. е. f_х =åΔх; f_у =åΔу.

Абсолютную линейную невязку вычисляют по формуле

.

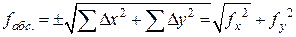Абсолютная невязка характеризует точность выполненных полевых работ, ее величина не должна превышать допустимую f_абс.≤ f_{абс доп} = 0,6мм М, где М – знаменатель масштаба съемки.

Для определения допустимости абсолютной невязки и оценки точности выполненных полевых работ вычисляют также относительную невязку, т.е. отношение абсолютной невязки f_абс. к периметру полигона (хода) ∑S. .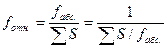

Допустимость невязки определяется заданной точностью и условиями местности и изменяется от 1/1000 – при неблагоприятных условиях измерений; 1/2000 – при средних условиях и 1/3000 – при благоприятных условиях измерений.

Таблица 7.1

Ведомость вычисления координат

Номер угла	Угол, β	Дирекц. угол, α (азимут)	Длина линии (горизонталь- ные пролож.) S, м	Приращение координат, м	Координаты, м
измеренный	исправл.	вычисленные	исправленные
град.	мин.	сек.	град.	мин.	град.	мин.	±	Δх	±	Δу	±	Δх	±	Δу	±	х	±	у
			-08
										+0,05		-0,01						0,00		0,00
								307,80	-	143,31	+	272,40	-	143,26	+	272,39
										+0,06		-0,02					-	143,26	+	272,39
								402,56	-	321,15	-	242,75	-	321,09	-	242,77
										+0,03		-0,01					-	464,35	+	29,62
								208,80	+	154,16	-	140,84	+	154,19	-	140,85
										+0,02							-	310,16	-	111,23
			-07					152,72	+	146,58	-	42,86	+	146,60	-	42,86
										+0,04		-0,01					-	163,56	-	154,09
								224,70	+	163,52	+	154,10	+	163,56	+	154,09		0,00		0,00
Σβизм.
Σβтеор.								1296,68
f β +0˚00΄15΄΄ угловая невязка		+ 464,26 + 426,50 + 464,35 + 426,48
	- 464,46 - 426,45 - 464,35 - 426,48
Fβдоп. = 3t√n = 1,5΄√5 = 3,35΄		Σ Δх= -0,20;Σ Δу= +0,05 0,00 0,00

Абсолютная невязка f_абс.=±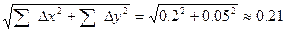

Относительная невязка f_отн.= .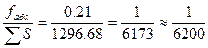

В случае допустимости полученной фактической абсолютной невязки, величины невязок f_x и f_y распределяются с обратным знаком пропорционально длинам сторон теодолитного хода. Для этого определяют долю поправки на каждые 100 м периметра полигона. То есть каждую из невязок f_x и f_y делят на значение длины полигона в сотнях метров и вычисляют поправки в каждое приращение пропорционально длине соответствующей линии. Поправки вводят со знаком обратным знаку невязки. Сумма поправок должна равняться невязке с обратным знаком. Поправки вводят в вычисленные приращения и получают исправленные приращения координат. Контроль уравнивания приращений: в замкнутом теодолитном ходе åΔх_уравн.= 0; åΔу_уравн.= 0.

Для вычисления координат точек теодолитного хода необходимо знать координаты исходного пункта. Если они не известны, то задаются условно. Координаты вычисляются в следующем порядке – координата последующей точки равна координате предыдущей точки плюс приращение между этими точками:

.

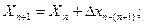
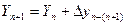Контролем вычисления координат в замкнутом теодолитном ходе служит получение координат исходного пункта.

Обработка материалов разомкнутого теодолитного хода имеет небольшие отличия от вычислений в разомкнутом ходе. Разомкнутые теодолитные ходы прокладываются между двумя твердыми сторонами, для которых известны дирекционные углы. В замкнутом теодолитном ходе обычно измеряются внутренние горизонтальные углы, а в разомкнутом – могут измеряться или левые или правые по ходу лежащие углы. Кроме того, измеряются примычные углы, которые образованы твердыми сторонами и сторонами хода.

Для разомкнутого теодолитного хода теоретическая сумма углов равна:

а) для измеренных правых по ходу углов

;

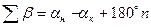б) для измеренных левых по ходу углов

,

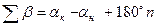где α_н и α_к – дирекционные углы начальной и конечной твердых сторон; n – число углов хода, включая и примычные.

Дирекционные углы сторон разомкнутого теодолитного хода вычисляют по следующим формулам:

а) для измеренных правых по ходу углов

;

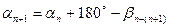б) для измеренных левых по ходу углов

,

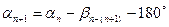где α_п+1 и α_n – дирекционные углы последующего и предыдущего направлений; β_n-(n+1) – горизонтальный угол, образованный последующим и предыдущим направлениями.

Контролем правильности вычисления дирекционных углов является получение известного дирекционного угла конечной твердой стороны.

Невязки в приращениях координат f_x и f_y в разомкнутом ходе определяются по формулам:

f_x=∑Δx_выч. - ∑Δx_теор.=∑Δx_выч. - (x_к - x_н);

f_y =∑Δy_выч. -_.∑Δy_теор.=∑Δx_выч. - (y_к - y_н),

где x_к. x_н. y_к. y_н. – абсциссы и ординаты соответственно известных конечной и начальной твердых точек хода.

Дальнейшая обработка выполняется аналогично, как и в замкнутом ходе. Контролем вычисления координат хода будет получение координат x_к и y_к конечного пункта.

Графическое оформление результатов теодолитного хода состоит в построении координатной сетки, нанесении точек теодолитного хода по координатам при помощи измерителя и поперечного масштаба и нанесении ситуации на план (см. п. 9.3).

7.4. Вычисление координат отдельных точек

Координаты отдельных точек, расположенных в стороне от теодолитных ходов, могут быть определены аналитически из угловых построений. Такие угловые построения на местности называются засечками. По расположению измеряемых углов относительно определяемого пункта (точки) засечки бывают прямыми, обратными и комбинированными.

Наиболее часто применяется прямая засечка, где угловые измерения выполняются одновременно с определением углов в теодолитных ходах.

Геодезическое построение, при котором в двух точках А и В с известными координатами Х_А; У_А; Х _В; У_В измеряются углы β₁ и β₂ между стороной АВ инаправлениями на определяемый пункт О, называется прямой засечкой (рис. 7.2).

Для определения координат пункта О прямой засечкой используют формулы Юнга:

; .

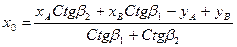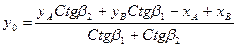Для более надежного и точного определения координат точки О используют двукратную засечку с пунктов А, В и С. Для этого на пунктах В и С измеряют углы β₃ и β₄. По известным координатам пунктов В и С и измеренным углам β₃ и β₄ вторично определяют координаты пункта О.