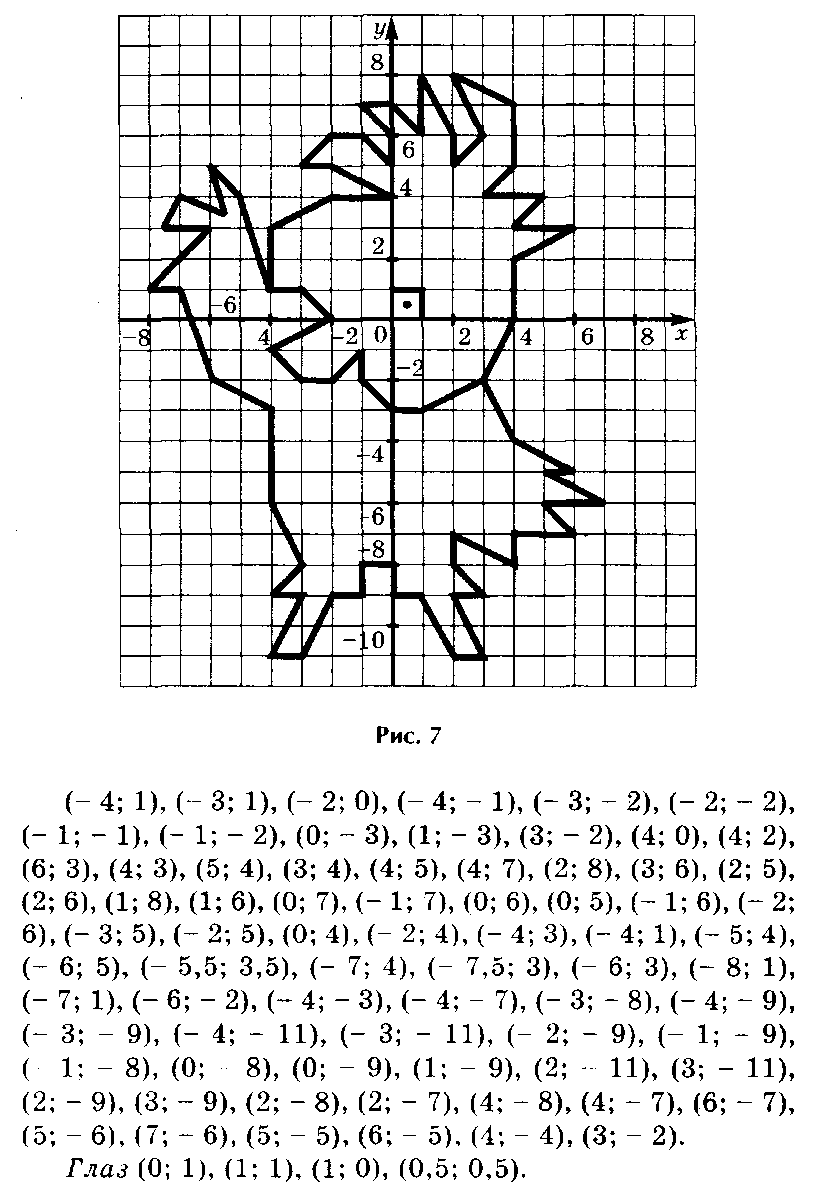
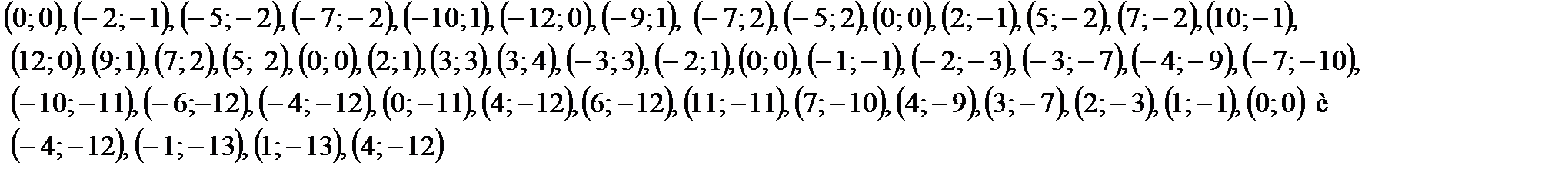Для того, чтобы определить положение какой-либо точки на плоскости необходимо знать две ее координаты. Для этого на плоскости строится система координат. Через данную точку О проводят две взаимно перпендикулярные прямые – х и у, которые иначе называются осями координат. Точку пересечения О называют – началом координат. Она служит началом отсчета единичных отрезков для каждой из осей.
Положительное направление показывают стрелками (ось Ох –“слева направо”, ось Оу – “снизу вверх”). Ось Ох –называют осью абсцисс, а Оу – ось ординат. Плоскость, на которой задана система координат, называется координатной плоскостью. Оси координат делят плоскость на четыре части, называемые координатными четвертями. Их нумеруют против часовой стрелки.
Определим положение точки на координатной плоскости. Пусть на координатной плоскости отмечена некоторая точка А(-3; 2). Проведем из нее перпендикуляр на ось Ох (ось абсцисс). Точка их пересечения на оси Ох имеет координату равную -3: х=--3. Число 3 называют абсциссой или первой координатой точки А.Проводим из точки А перпендикуляр к оси Оу (оси ординат), получаем, что ордината (или вторая координата) точки А равна 2: у = 2.Числа -3 и 2 определяют положение точки А на координатной плоскости. Их называют координатами точки на плоскости. Указать только одну координату точки недостаточно, так как абсциссу х=-3 имеют еще и другие точки,также обстоит дело с ординатой точки. Координаты точки записывают в скобках: А (х;у), пример В() При этом абсцисса точки всегда пишется на первом месте, а ордината - на втором. Описанная система координат называется прямоугольной. Часто также ее называют декартовой системой координат в честь французского философа и математика Рене Декарта, который впервые применил ее в своих исследованиях.
ТЕСТ по теме «Координатная плоскость»
1) Под каким углом пересекаются координатные прямые, образующие систему координат на плоскости?
- Под острым углом
- Под прямым углом
- Под тупым углом
- Под развернутым углом
2) Как называется горизонтальная прямая?
- Аппликата
- Ордината
- Абсцисса
- Биссектриса
3) Как называется вертикальная прямая?
- Ордината
- Абсцисса
- Аппликата
- Биссектриса
4) Как называют точку пересечения этих прямых?
- Начало всех начал
- Середина
- Начало отсчета
- Разделитель
5) Как называют пару чисел, определяющих положение точек на плоскости?
- Координаты точки
- Числа на плоскости
- Числа для точки
- Показатели точки
6) Что показывают стрелки на координатных прямых?
- Что прямые можно продолжить
- Положительное направление
- Отрицательное направление
- Ничего не показывают
7) В какой координатной четверти может находится точка, имеющая координаты с разными знаками?
- В 1 или во 2
- Только во 2
- Во 2 или в 3
- Во 2 или в 4
8) Как правильно записываются координаты?
- (х;у)
- (у;х)
- х, у
- В любом порядке
Практическая часть.
Участники представляют свои работы:
а) Изображение на координатной плоскости созвездий Малой медведицы и Большой медведицы. Рассказывают легенду об этих созвездиях.
Мифов о созвездиях очень много. Познакомимся с несколькими из них: Созвездия Большой и Малой Медведиц. Ревнивая Юнона превратила Каллисто в медведицу и спрятала в горах Аркадии. У Каллисто родился медвежонок-сын Аркад. Когда Юпитер, наконец, нашел возлюбленную с ребенком, в награду за страдания, которые им выпали, он перенес медведицу и медвежонка на небо.
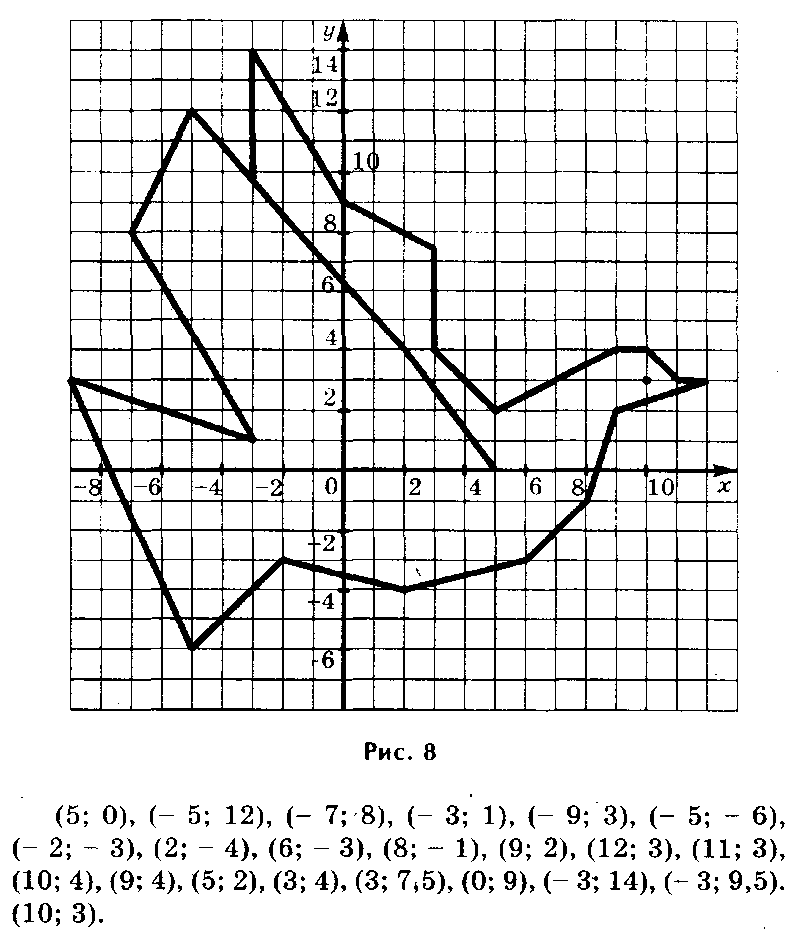
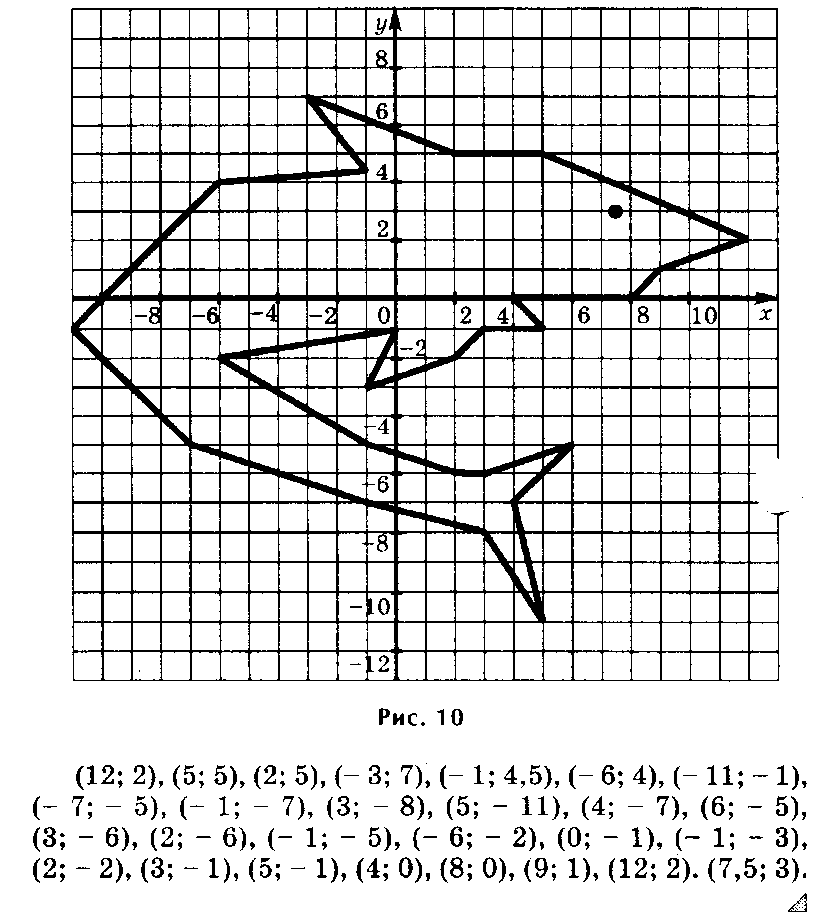
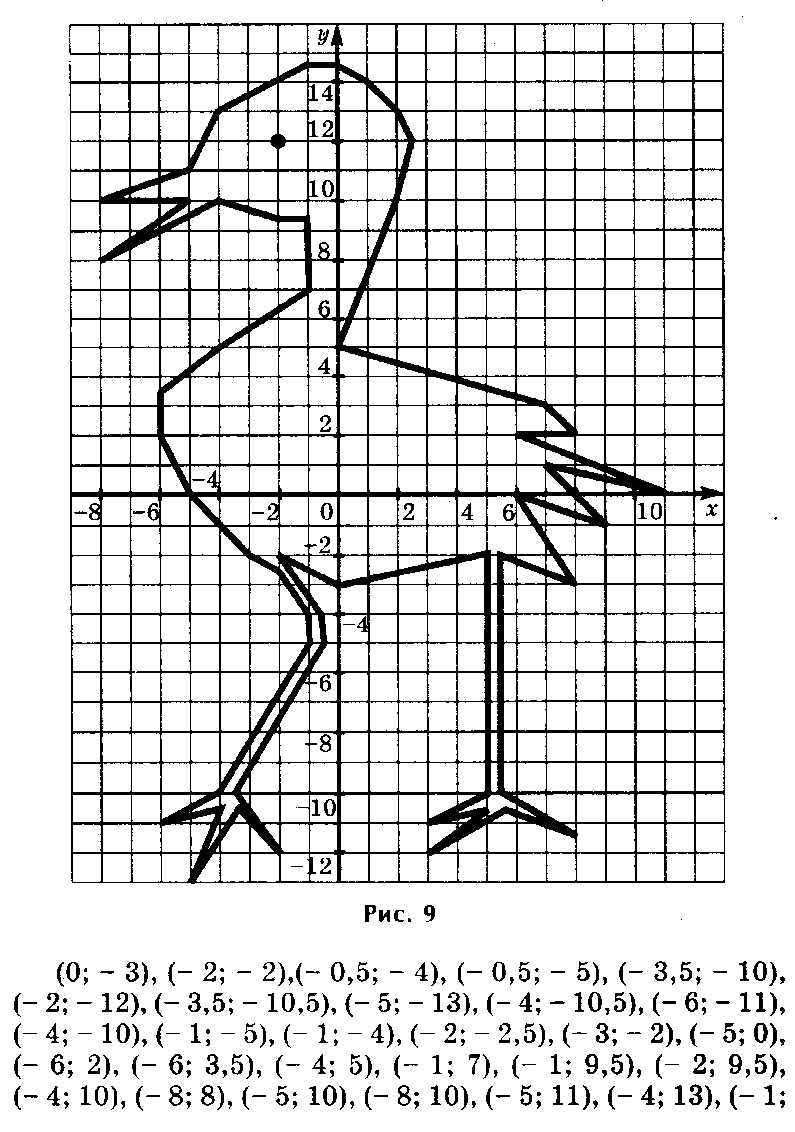
б) Показывают рисунки, построенные по координатам точек.
в) Показывают построенный график изменения температуры в течение суток 26 апреля.
Вывод: Всё живое и неживое во Вселенной имеет свои координаты
Приложения.
Рисуем по координатам.
| «Рыбка». (3; 3); (0; 3); (-3; 2); (-5;2); (-7;4); (-8;3); (-7;1); (-8;-1); (-7;-2); (-5;0); (-1;-2); (0;-4); (2;-4); (3;-2); (5;-2); (7;0); (5;2); (3;3); (2;4); (-3;4); (-4;2); глаз(5;0). | . «Утёнок».(3; 0); (1; 2); (-1;2); (3;5); (1;7); (-3;6); (-5;7); (-3;4); (-6;3); (-3;3); (-5;2); (-5;-2); (-2;-3); (-4;-4); (1;-4); (3;-3); (6;1); (3;0); глаз (-1;5). |
Белочка | (1;-4) | (-1;0) | (-3;3) | (9;0) | | (1;-6) | (-3;0) | (-1;4) | (9;-4) | | (-4;-6) | (-3;-1) | (0;6) | (6;-4) | | (-3;-5) | (-4;-1) | (1;4) | (5;-1) | | (-1;-5) | (-4;0) | (1;2) | (4;-1) | | (-3;-4) | (-3;1) | (3;4) | (1;-4) | | (-3;-3) | (-1;1) | (6;5) | (-1;3) | | (-1;-1) | (-1;2) | (9;2) | Глаз | | «Медвежонок» | (-4;5) | (0;7) | (2;-3) | (-2;-1) | | (-3;5) | (1;7) | (3;-4) | | | (-3;6) | (2;6) | (2;-4) | (-6;-1) | | (-2;7) | (2;4) | (1;-8) | (-3;1) | | (-1;7) | (1;3) | (-2;-8) | (-2;2) | | (-1;8) | (1;2) | (-1;-7) | (-2;3) | | (0;8) | (2;1) | (-1;-3) | (-3;3) | | | | | (-4;4) (-4;5) | | | | | (-2;5) | | | | | Глаз | |
Постройте в одной координатной плоскости созвездие “Малой Медведицы”:
(6; 6), (3; 7), (0; 8), (-3; 6), (-6; 4), (-8; 6), (-5; 8), (-3; 6)
и “Большой Медведицы”:
(-15; -5), (-10; -3), (-6;-3), (-3; -4), (6; -4), (5; -8), (-1; -8), (-3; -4).
Лиса | (-5;-5) | (1;5) | (5;4) | (-4;-3) | | (-4;5) | (1;4) | (6;2) | (-5;-3) | | (-3;6) | (0;3) | (6;0) | (-3;-1) | | (-2;6) | (0;2) | (3;-3) | (-4;0) | | (-1;7) | (2;0) | (-1;-3) | (-4;3) | | (-1;6) | (2;-1) | (-1;-2) | (-3;4) | | (0;6) | (4;3) | (-2;-1) | (-3;5) | | | | | Глаз | | Рыбка | (3;3) | (-8;-1) | (7;0) | | (0;3) | (-7;-2) | (5;2) | | (-3;2) | (-5;0) | (3;3) | | (-5;2) | (-1;-2) | (2;4) | | (-7;4) | (0;-4) | (-3;4) | | (-8;3) | (3;-2) | (-4;2) | | (-7;1) | (5;-2) | (5;0) | | | | Глаз | |
Белочка | (-2;4) | (2;-3) | (10;4) | (-2;-4) | | (0;6) | (5;4) | (3;-6) | (-1;0) | | (0;5) | (7;5) | (2;-6) | (-4;0) | | (1;6) | (7;6) | (0;-7) | (-1;1) | | (1;5) | (8;7) | (-4;-7) | (-1;2) | | (2;3) | (9;7) | (-1;-6) | (-2;3) | | (1;2) | (10;6) | (-2;-5) | (0;4) | | | | | Глаз | | Зайчик | (1;7) | (-8;0) | (-1;3) | (3;5) | | (0;10) | (-9;1) | (0;-2) | (2;6) | | (-1;11) | (-9;0) | (1;-2) | (1;9) | | (-2;10) | (-7;-2) | (0;0) | (0;10) | | (0;7) | (-2;-2) | (0;3) | (1;6) | | (-2;5) | (-3;-1) | (1;4) | Глаз | | (-7;3) | (-4;-1) | (2;4) | | |
Дракоша

----------------------------------------------------------------------------------------------------------------------------------------
Лебедь
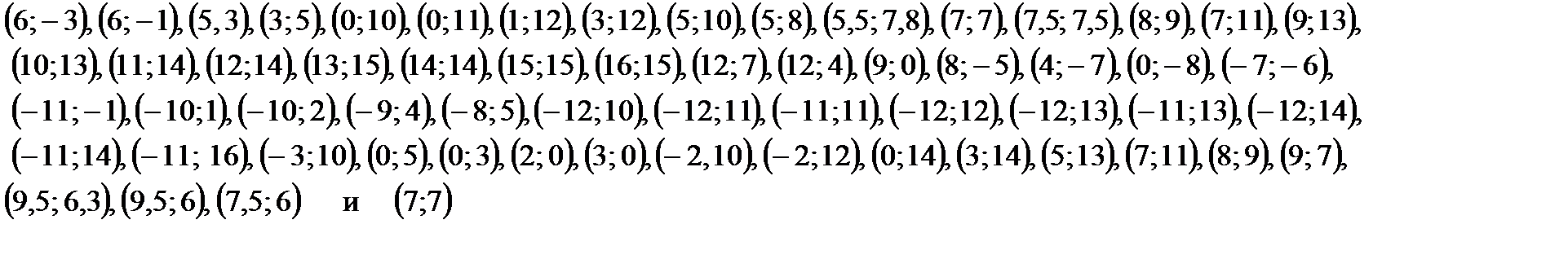
------------------------------------------------------------------------------------------------------------------------------------------
Змейка
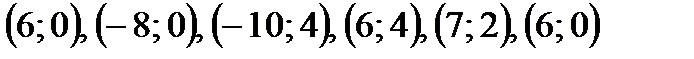 и
и 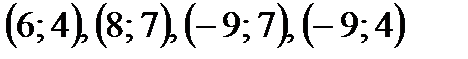 и
и 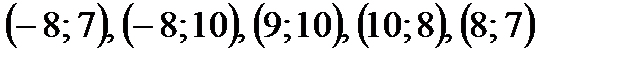
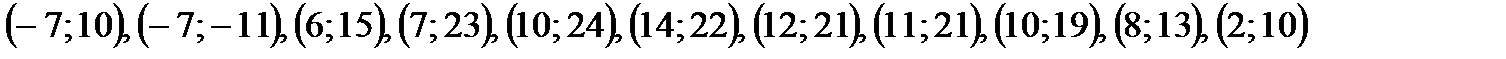 и
и
 и
и  и
и 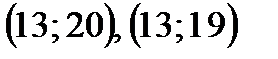
Бегемот
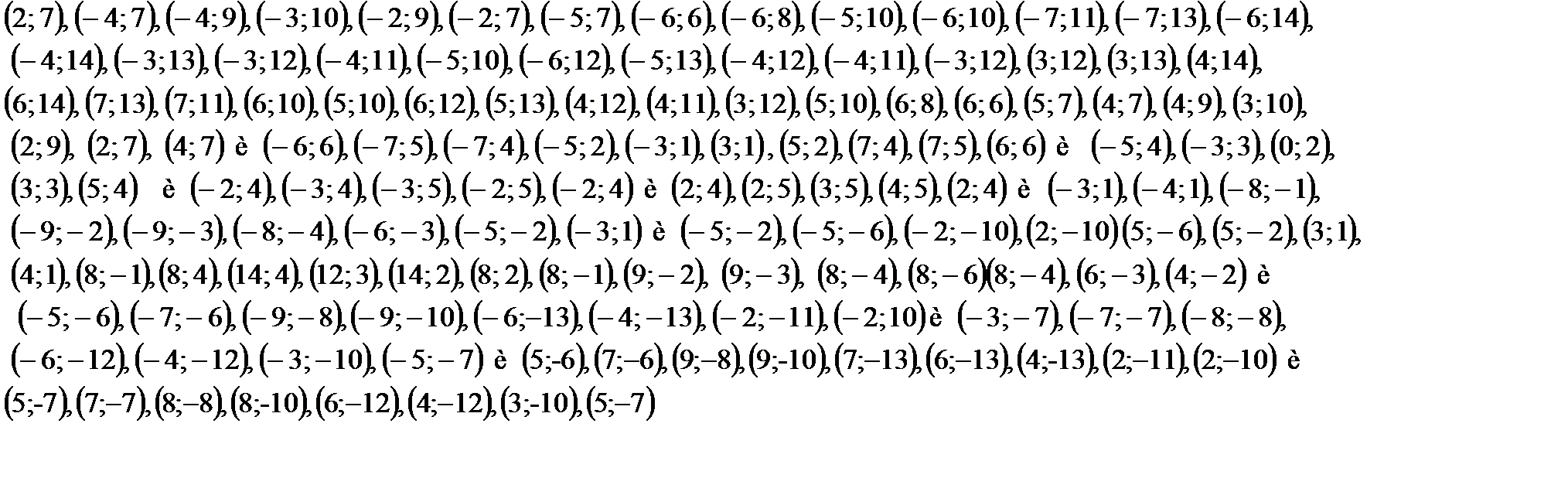 -----------------------------------------------------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------------------------------------------------
П 45
Колокольчик
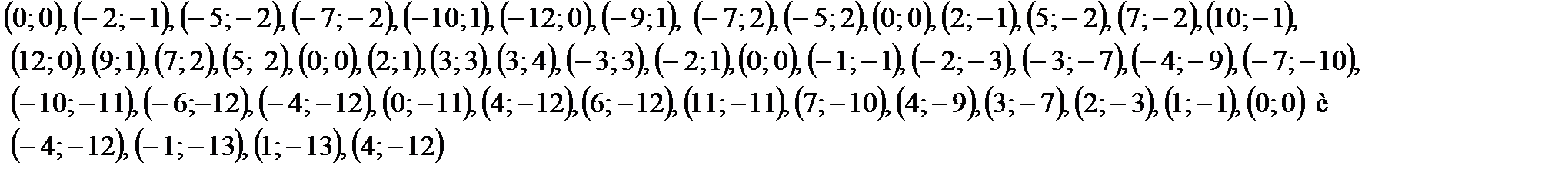
-------ДОПОЛНИТЕЛЬНЫЕ ЗАДАНИЯ------------------------------------------
| | | | |
| 1. –2х + 19 = 5х – 16 (х; 1) 2. 8х – 25 = 3х + 20 (х; 0) 3. 6 – у = 3(3у – 8) (5; у) 4. 5(у + 1,2) = 7у + 4 (1; у) 5. 4(х – 3) – 16 = 5(х – 5) (х; 3) 6. 3х – 17 = 8х + 18 (х; 0) 7. 11 – 5у = 12 – 6у (–3; у) 8. 4у + (11,8 – у) = 3,8 – 5у (1; у) 9. 3х + 16 = 8х – 9 (х; 1) | 1. 3х + 5 = 8х – 15 (х; 0) 2. 3х + 16 = 8х – 9 (х; 4) 3. 4 + 25у = 6 + 24у (2; у) 4. 4(х – 3) – 16 = 5(х – 5) (х; 3) 5. 5х + 27 = 4х + 21 (х; 0) 6. 4(3 – 2у) – 42 = 2(3 + 2у) (–3; у) 7. 3(4х – 8) = 3х – 6 (х; –2) 8. 1 – 5(1,5 + х) = 6 – 7,5х (х; –4) 9. 3(5 – х) + 13 = 4(3х – 8) (х; 0) | 1. 15х – 3 = 10х + 12 (х; 1) 2. –2х – 25 = –5х – 7 (х; 1) 3. 4(5 – 2у) = 2(1 – у) (3; у) 4. 3у + 16 = 8у – 9 (1; у) 5. 4х + (11,8 – х) = 3,8 – 5х (х; 1) 6. 3у + 2(2у – 3) = 8 – 7(у – 2) (–7; у) 7. 2 – 5х = х + 14 (х; –3) 8. 5(у – 7) = 3(у – 4) – 29 (2; у) 9. 11 – 5у = 12 – 6у (3; у) | |
| Соедините последовательно точки, координаты которых узнаете, решив все уравнения: | Соедините последовательно точки, координаты которых узнаете, решив все уравнения: | Соедините последовательно точки, координаты которых узнаете, решив все уравнения: | |
| | | | |
| 1. –12х – 3 = 11х – 3 (х; 2) 2. 1,4 – 0,6у = 0,7 – 0,5у (2; у) 3. 16 – 3х = 4 – 7х (х; 2) 4. 4х + (11,8 – 3х) = 5,8 – 5х (х; 0) 5. 4у + 12 = 3у + 8 (–5; у) 6. 3(4х – 5) = 3х – 6 (х; –2) 7. 3у – 17 = 8у + 18 (6; у) 8. 0,18х – 2,83 = 0,19х – 2,89 (х; –4) 9. 5(у + 7) = 3(у + 4) + 27 (0; у) | |
| 1. 6х + 10 = 4х + 12 (х; 3) 2. 7х + 25 = 10х + 16 (х; 6) 3. 3у + 16 = 8у – 9 (5; у) 4. 0,4(6у – 7) = 0,5(3у + 7) (5; у) 5. 4(2 – х) = 7(2х – 4) (х; 8) 6. 3(2х – 1) + 7 = 4 (х; 6) 7. 5у – 7 = 11 + 2у (–1; у) 8. 9,6 – (2,6 – х) = 4 (х; 8) 9. 1,7 – 0,6у = 0,3 – 0,4у (–6; у) 10. 17 – 4х = 5 – 6х (х; 5) 11. 2,8 – 3,2х = –4,8 – 5,1х (х; 6) 12. 0,2(5х – 2) = 0,3(2х – 1) – 0,9 (х; 3) 13. 2у – 1,5(у – 1) = 3 (1; у) 14. 1 – 5(1,5 + х) = 6 – 7,5х (х; –4) 15. 3у – 18 = 8у + 17 (4; у) 16. 4(1 – 0,5х) = –2(3 + 2х) (х; –7) 17. 5х + 27 = 4х + 21 (х; –4) 18. у – 15 = 4(3 – 2у) (–2; у) | 1. 3(х – 5) + 10 = 2(3 + х) – 14 (х; 1) 2. 1,2(2х – 4) + 0,6 = 3х – 3,6 (х; 1) 3. 16у – 4 = 12у + 8 (–1; у) 4. 5(7 – 2х) + 13 = 9х + 48 (х; 3) 5. 4(3 – 7у) + 10 = –10у – 86 (–1; у) 6. 6у – 72 = 4у – 56 (0; у) 7. 5х + (13,4 – 2х) = 16,4х (х; 5) 8. 12 – (4х + 5) = 7 + х (х; 3) 9. 5(2х – 3) + 11 = 6х (х; 3) 10. –2(7 – у) + 13 = у (1; у) 11. 5 – 3(2х – 1) = 4х – 22 (х; 1) 12. 1,2х – 7 = 6х – 16,6 (х; 0) 13. 2(1,2у + 5) – 1 = 2у + 6,6 (2; у) 14. 1,7х + 0,9 = 2х (х; –7) 15. 9 – 2(х + 4) = 2х + 13 (х; –7) 16. –4(2 + 3х) + 11 = –15х – 3 (х; –6) 17. 5у + 12 = –3у + 12 (–2; у) 18. 0,2(3у + 2) = 2,6у – 1,6 (–3; у) | |
| Соедините последовательно точки, координаты которых узнаете, решив все уравнения: | |
| | |
| 1. 6 – 2у = 8 – 3у (1; у) 2. 15х + 3 = 10х – 12 (х; 2) 3. –5х – 11 = –6х – 12 (х; –1) 4. 3х + 5 = 8х – 15 (х; –1) 5. 5(х + 3) = 27 + 3х (х; 2) 6. 3у + (4 – 2у) = 6 (1; у) 7. 5у – (13 + у) = у + 14 (1; у) 8. 3(2х – 4) – 2(х + 3) = –2 (х; 4) 9. 4у – 3 = 2(7 – у) + 1 (1; у) | |

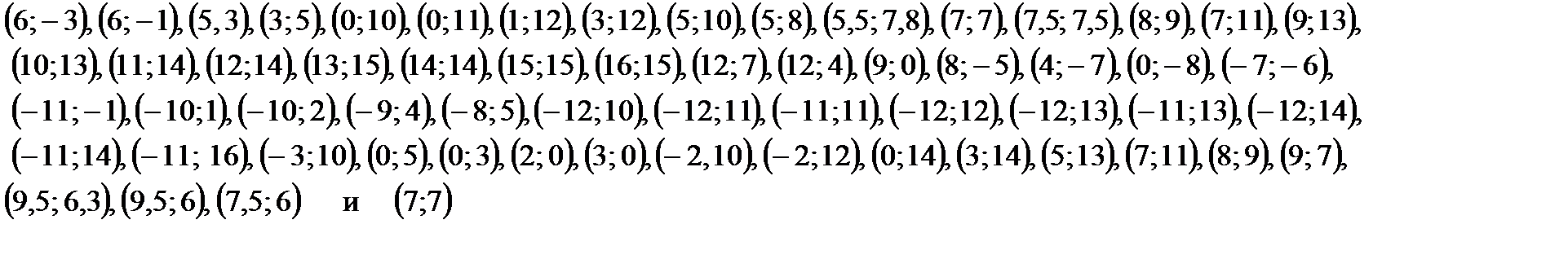
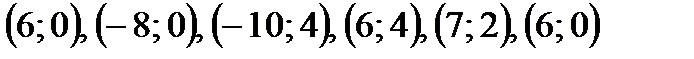 и
и 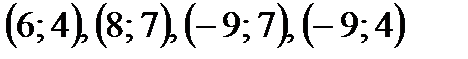 и
и 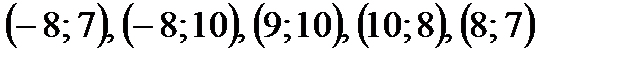
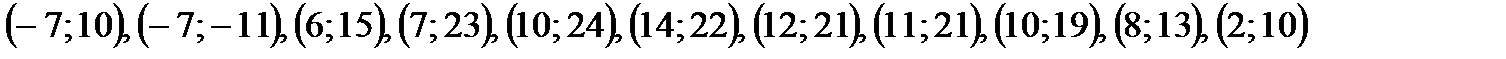 и
и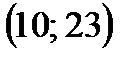 и
и 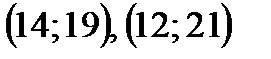 и
и 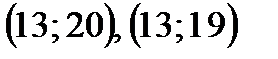
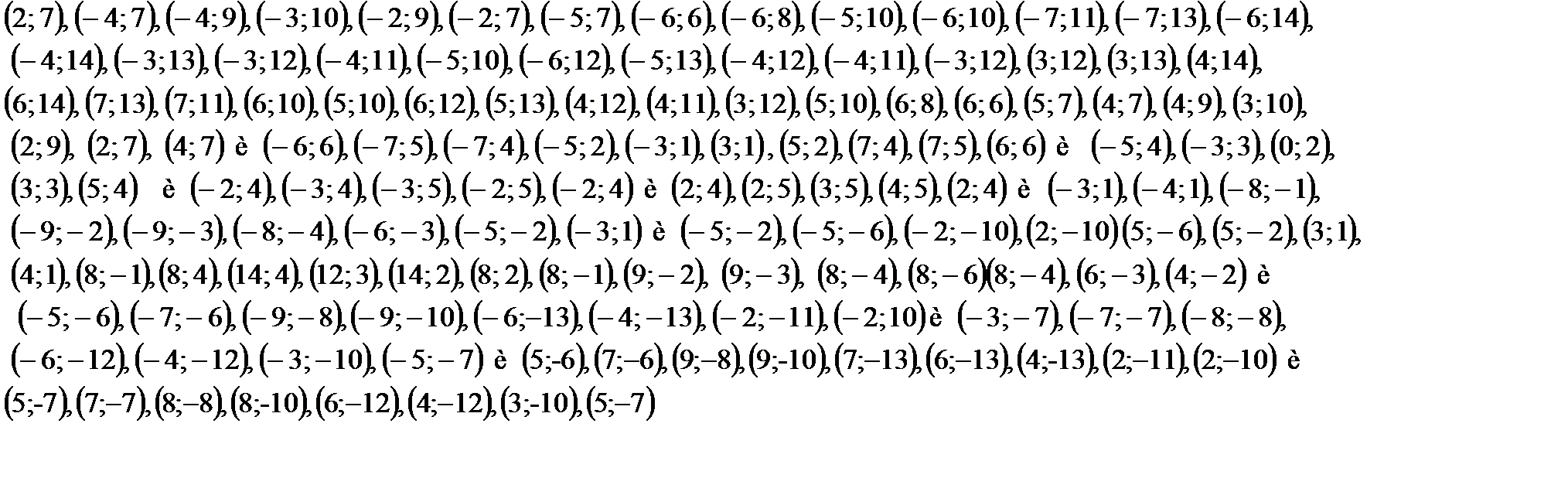 -----------------------------------------------------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------------------------------------------------