Методы сравнения статистических совокупностей
Организация научного исследования и его основные этапы
Выделяют 4 этапа статистического исследования.
1-й этап
— определение целей и задач, составление плана и программы исследования;
Й этап
— наблюдение, сводка и группировка полученных статистических материалов, вычисление первичных итогов;
2-й этап – в первую очередь сбор данных:
а) Непосредственное наблюдение (измерение жизненной емкости легких, форсированного выдоха, параметров кардиограмм и т.п.).
б) Выкопировка данных из отчетно-учетной документации предполагает использование в виде источника информации различных документов (история болезни, история развития ребенка, больничный лист).
в) Опрос обеспечивает получение информации со слов опрашиваемого (респондента) методом интервью или заочным путем (почтовые, телефонные, прессовые опросы).
Генеральная и выборочная совокупность.
Репрезентативность
Объектом наблюдения описательной статистики является статистическая совокупность, состоящая из отдельных предметов или явлений – единиц наблюдения. Статистическая совокупность, подлежащая исследованию, называется генеральной совокупностью. Теоретически генеральная совокупность может быть безгранична.
Выборочная совокупность (выборка) – подмножество (часть) генеральной совокупности, получаемое посредством случайного отбора. Смысл выборочного метода состоит в том, что извлечение из некоторой весьма пространной (или вообще беспредельной) генеральной совокупности несравненно меньших по объему выборок резко экономит время обработки данных. Процесс случайного отбора данных называется процессом рандомизации (random – «случайный»).
Репрезентативность выборочной совокупности – свойство выборки корректно отражать генеральную совокупность.
Одна и та же выборка может быть репрезентативной и нерепрезентативной для разных генеральных совокупностей. Например, выборка, целиком состоящая из пациентов, больных сахарным диабетом, не репрезентирует всех пациентов больницы, но может отлично отображать пациентов-диабетиков.
Выделяют репрезентативность количественную и качественную (структурную). Количественная репрезентативность определяется числом наблюдений, гарантирующим получение статистически достоверных данных. В общем, здесь действует основной постулат закона больших чисел — «чем больше наблюдений — тем результаты достоверней» или «чем больше число наблюдений, тем больше значения характеристик выборки приближаются к соответствующим характеристикам генеральной совокупности».
Качественная репрезентативность — обозначает структурное соответствие выборочной и генеральной совокупностей. Например: если в составе генеральной совокупности 50% — лица мужского пола, то и в выборочной группе их должно быть 50%.
3-й этап
— углубленная математико-статистическая обработка данных;
4-й этап
— анализ полученных результатов, выводы.
Относительные величины.
Относительные величины – дробь, отношение двух абсолютных показателей. Не имеют размерности. Они вычисляются в том случае, когда необходимо сравнить явления, происходящие одновременно или отстоящие друг от друга по времени (пример: сравнение заболеваемости населения в г.Красноярске и заболеваемости в г.Ачинске; сравнение уровней рождаемости 2000 и 2011 гг.). Относительные величины широко используются в официальной статистике для оценки медико-демографической и санитарно-эпидемиологической ситуации, оценки деятельности медицинских учреждений и т.п. Среди относительных величин наибольшее практическое значение имеют: интенсивные коэффициенты, экстенсивные коэффициенты.
Интенсивные коэффициенты показывают интенсивность развития (частоту, уровень, распространенность, риск) явления в среде, которая продуцирует это явление. Эти коэффициенты отвечают на вопрос, как часто явление встречается в известной среде. Например: явление – количество заболевших за год относим к среде, его продуцирующей – численности населения.
Общая формула для расчета интенсивного показателя выглядит следующим образом:
Масштабирующий коэффициент применяется для удобства интерпретации полученных результатов. Его размер тем больше, чем меньше расчетное значение относительной величины. Масштабирующий коэффициент может принимать различные значения: 100, 1000, 10000 и т.д., и отражает численность населения, на которую рассчитывается показатель. Чем реже явление встречается в среде, тем большее значение масштабирующего коэффициента приходится выбирать. В ряде случаев принято использовать определенные масштабирующие показатели; например: общая заболеваемость всегда рассчитывается на 1000 человек населения.
Вычисление и анализ этих коэффициентов является основой медицинских исследований, проводимых на уровне больших групп населения, населенных пунктов, городских и сельских районов, областей и регионов.
Интенсивные величины используются для характеристики смертности, рождаемости, заболеваемости, обеспеченности (врачами, койко-местами и т.д.).
Для графического представления интенсивных коэффициентов используются различные варианты столбиковых и линейных диаграмм. Для отображения циклических явлений наглядными являются радиальные диаграммы.
Экстенсивные коэффициентыхарактеризуют долю части явления по отношению к явлению в целом и отражают его структуру. Они всегда выражаются в процентах. Пример: из общего количества госпитализированных в хирургическое отделение 35% пришлось на больных с острым аппендицитом, 25% - на больных с паховой грыжей, 20% - на больных с желчекаменной болезнью, 15% - на больных с осложнениями язвенной болезни желудка, 5% - на больных с другими диагнозами. Рассчитываются:
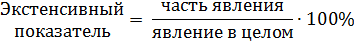
Для графического представления экстенсивных коэффициентов используют внутрисекторную или внутристолбиковую диаграммы.
Средние величины.
Вариационный ряд– ряд числовых измерений какого-либо признака, отличающихся друг от друга по своей величине и расположенных в определенном порядке (возрастания или убывания). Каждое числовое значение в вариационном ряду называют вариантой.
Средняя величина– показатель, погашающий индивидуальные различия значений вариант, позволяя сравнивать разные совокупности между собой. Основными средними величинами являются среднее арифметическое, мода, медиана.
Пусть имеется n объектов, для которых измерена некоторая характеристика, и получены значения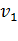 
, 
, ..., 
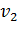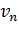. Среднее арифметическое этих n значений обозначают через М и определяют как
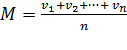
Медиана. Если все элементы совокупности размещены в порядке возрастания или убывания числовых значений признака, то медиана – это такое значение признака, которое делит всю совокупность пополам (стоит в середине вариационного ряда). Обозначается символом Ме.
Если объем совокупности нечетный и равен (2n+1), и варианты размещены в порядке возрастания их значений:
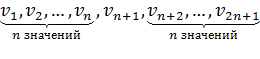
то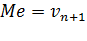 
.
Если же количество элементов четное и равно 2n, то нет варианты, которая бы делила совокупность на две равные по объему части:
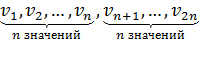
поэтому в качестве медианы условно берется полусумма вариант, находящихся в середине вариационного ряда:
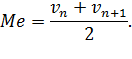
Медиана обладает важными свойствами, которые в некоторых случаях дают ей преимущество перед другими средними величинами. Например, если при упорядоченном размещении некоторого признака "крайние" значения сомнительные и к тому же резко отличаются от основной массы данных, то в качестве меры центральной тенденции целесообразно использовать медиану. Это связано с тем, что на ее величину эти "крайние" значения никакого влияния не оказывают, а в то же время они могут существенным образом повлиять на значение среднего арифметического.
Среднее арифметическое является хорошей мерой центральной тенденции для количественных данных, не имеющих выбросов; медиана - для порядковых данных и для количественных данных, в том числе и при наличии выбросов. Подобная характеристика нужна и для номинальных данных. Такой характеристикой является мода. Она применяется как для неупорядоченных категорий, так и для упорядоченных, и для количественных данных.
Мода – это такое значение признака, которое встречается наиболее часто. В случае дискретных рядов вычислить моду нетрудно. Достаточно найти варианту, которая встречается наиболее часто, это и будет мода. Будем обозначать моду символом Мо. Если все значения в вариационном ряде встречаются одинаково часто, то считают, что этот ряд не имеет моды.
Виды распределений.
Нормальное (Гауссово, симметричное, колоколообразное) распределение– одно из самых важных распределений в статистике. Оно характеризуется тем, что наибольшее число наблюдений имеет значение, близкое к среднему, и чем больше значения отличаются от среднего, тем меньше таких наблюдений. Примерами характеристик, подчиняющихся нормальному распределению, являются показатели роста, веса, какие-либо биохимические показатели крови.
Гауссово распределение характеризует распределение непрерывных случайных величин и встречается в природе наиболее часто, за что и получило название «нормального».
Кривая нормального распределения имеет следующие свойства:
· колоколообразна (унимодальна);
· симметрична относительно среднего;
Среднее арифметическое, мода и медиана при нормальном распределении равны и соответствуют вершине распределения:
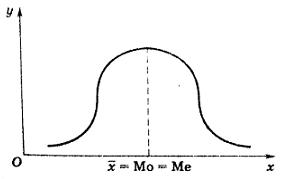
Методы сравнения статистических совокупностей.
Сравнение
От вида распределения (нормальное или нет) и типа исследуемого признака (данные количественные или качественные) зависит выбор подходящего критерия сравнения. Критерии делятся на два типа – параметрические (критерии Стьюдента, Фишера, Пирсона) и непараметрические (критерии Манна-Уитни, Вилкоксона, z-критерий). Параметрические критерии применяются только в случае нормального распределения данных. Если распределение отличается от нормального, то следует пользоваться непараметрическими критериями.
Если признаки количественные (выражены численно), то для сравнения данных применяются критерий Стьюдента, Манна-Уитни или Вилкоксона.
Если признаки качественные (характеризуют свойство), то для сравнения данных применяются критерий хи-квадрат (критерий Пирсона) или Z-критерий.
Корреляция
Корреляция – зависимость одного явления от другого.
Расчет коэффициентов корреляции дает численную характеристику того, насколько связаны явления друг с другом. Основными коэффициентами корреляции являются коэффициент корреляции Пирсона и коэффициент корреляции Спирмэна.
Свойства коэффициентов корреляции r:
• Значения коэффициента корреляции изменяются в пределах от -1 до +1.
• Знак коэффициента корреляции показывает направление связи, увеличивается (положительный r, прямая связь) или уменьшается (отрицательный r, обратная связь) одна переменная, по мере того как увеличивается другая. Например, при увеличении возраста ребенка сила скелетной мускулатуры увеличивается (прямая корреляционная связь). В зрелом возрасте такой связи уже нет. А в старших возрастных группах тенденция становится обратной (обратная корреляционная связь).
• Величина коэффициента корреляции указывает, насколько сильно связаны явления. Чем ближе коэффициент корреляции r к крайним точкам (±1), тем больше степень связи.
Сила корреляционной связи между признаками оценивается по величине коэффициента корреляции согласно Таблице 1:
Таблица 1
Распределение значений коэффициента линейной корреляции
|
Функциональная зависимость – такой вид зависимости, когда каждому значению одного признака соответствует точное значение другого (зависимость может быть задана функцией).