Картографические проекции. Определение, классификации.

Картографическая проекция - это математически определенное отображение поверхности эллипсоида планеты или шара на плоскость карты

Проекция устанавливает однозначное соответствие между геодезическими координатами точек ( широтой B и долготой L) и их прямоугольными координатами Х и У на карте:

Х = f₁(B, L); Y = f₂(B, L)

B –широта, L – долгота

Х и Y – прямоугольные координаты

Конкретные реализации функций f₁ и f₂ часто выражены сложными математическими зависимостями, а их число практически не ограничено, а следовательно разнообразие картографических проекций огромно.

В зависимости от положения оси системы сферических координат, используемой при проецировании, различаются:

Нормальная система – ось сферических координат совпадает с осью вращения Земли

Поперечная система – ось сферических координат лежит в плоскости экватора

Косая система – ось сферических координат расположена под углом к оси вращения Земли

Картографические проекции классифицируются по характеру искажений, по виду вспомогательной поверхности, по виду нормальной картографической сетки (параллелей и меридианов), по ориентировке вспомогательной поверхности относительно полярной оси и т.д

Классификация проекций по характеру искажений. Показатели искажений.

Равновеликие - площади без искажений, искажаются углы и формы.

Равноугольные - углы и формы сохраняются, используются на нафигационных картах

Равнопромежуточные - произвольные проекции,в которых масштаб длин по одному из главных направлений постоянен и обычно равен главному масштабу карты. Различают равнопромежуточные по меридианам или по параллелям.

Произвольные проекции - все остальные виды проекций,в которых в тех или иных соотношениях искажаются и площади и углы.

По виду нормальной картографической сетки проекции подразделяются на следующие классы.

Азимутальные - поверхность земного шара (эллипсоида) переносится на касательную или секущую плоскость. В зависимости от расположения плоскости по отношению к земной оси азимутальные проекции бывают:

Нормальные (полярные, прямые) – плоскость перпендикулярна к оси вращения Земли,

Поперечные (экваториальные) – плоскость проекции перпендикулярна к плоскости экватора,

Косые (горизонтальные) – плоскость проекции располагается под острым углом к плоскости экватора (рис.4.5).

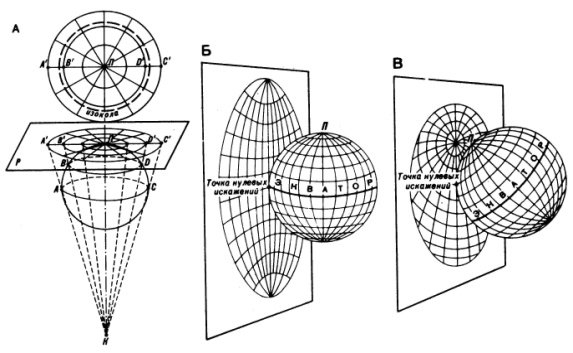
Рис.4.5. Виды азимутальных проекций:

а) нормальная, б) поперечная, в) косая.

Цилиндрические – поверхность эллипсоида (шара) проектируется на поверхность касательного или секущего цилиндра, а затем его боковая поверхность разворачивается в плоскость (рис.4.6). Различают:

нормальные (прямые) цилиндрические проекции – ось цилиндра

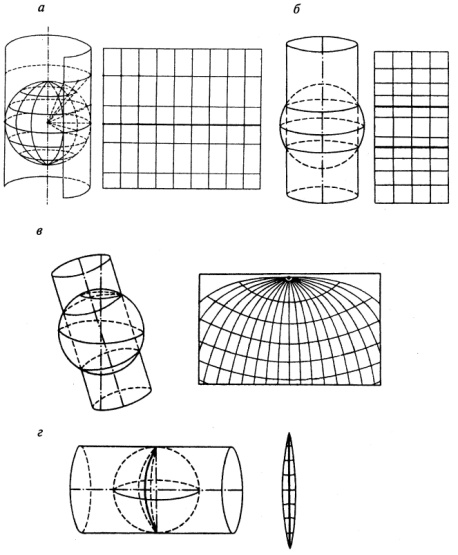
Рис.4.6. Цилиндрические проекции

а – нормальная цилиндрическая проекция на касательном цилиндре;

б – нормальная цилиндрическая проекция на секущем цилиндре;

в – косая цилиндрическая проекция на секущем цилиндре;

г – поперечная цилиндрическая проекция на касательном цилиндре.

совпадает с осью Земли, меридианы изображаются равноотстоящими параллельными прямыми, а параллели – перпендикулярными к ним прямыми;

поперечные цилиндрические проекции – ось цилиндра располагается в плоскости экватора (рис.4.6г), цилиндр касается шара по меридиану, искажения вдоль него отсутствуют;

косые цилиндрические проекции – ось цилиндра располагается под острым углом к поверхности экватора (рис.4.6в). В поперечных и косых проекциях параллели и меридианы, исключая средний, имеют вид кривых линий. Примером поперечной цилиндрической проекции является проекция Гаусса-Крюгера, удобной для проектирования геодезических зон.

Конические проекции – поверхность эллипсоида (шара) переносится на поверхность касательного или секущего конуса (рис.4.7).

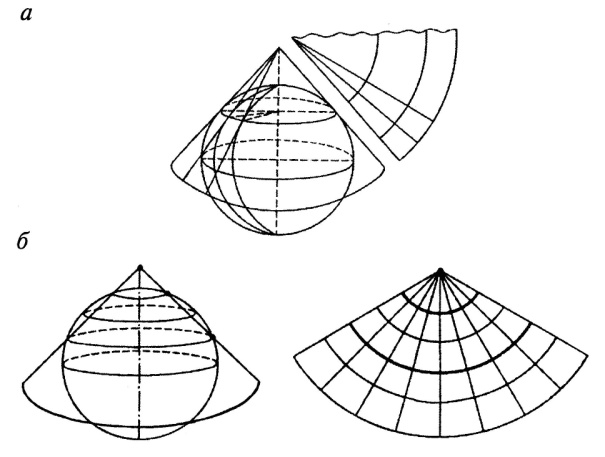
Рис.4.7. Нормальная коническая проекция

а - проекция на касательном конусе и развертка

б – проекция на секущем конусе и развертка

Как и в предыдущих проекциях, выделяют нормальную (прямую) коническую проекцию – ось конуса совпадает с осью вращения Земли, поперечную коническую – ось конуса лежит в плоскости экватора и косую коническую – ось конуса располагается под углом к плоскости экватора

Поликонические проекции – проекции, в которых сеть меридианов и параллелей переносится на несколько конусов, каждый из которых развертывается в плоскость. Многогранные проекции – проектирование эллипсоида (шара) ведется на поверхность касательного или секущего многогранника.

Условные проекции – проекции, которые строят по заданным условиям, например, для получения определенного вида географической сетки, заданного характера искажений и др. К ним относятся псевдоцилиндрические, псевдоконические, псевдоазимутальные и другие проекции, строящиеся посредством преобразования исходных проекций.

Псевдоцилиндрические проекции – проекции, в которых экватор и параллели – прямые, параллельные друг другу (что роднит их с цилиндрическими проекциями), а меридианы, кроме среднего, кривые линии, увеличивающие свою кривизну по мере удаления от среднего меридиана.

Псевдоконические проекции – проекции, в которых параллели представляют собой дуги концентрических окружностей (как и в нормальных конических), а меридианы – кривые линии, симметрично расположенные относительно среднего прямолинейного меридиана, кривизна их увеличивается с удалением от среднего меридиана

Псевдоазимутальные проекции – проекции, в которых параллели представляют концентрические окружности, а меридианы – кривые, сходящиеся в точке полюса и симметричные относительно одного или двух прямолинейных меридианов.

Круговые проекции – меридианы, исключая средний, и параллели, исключая экватор, изображаются дугами эксцентрических окружностей. Средний меридиан и экватор – прямые. Примером круговой проекции является проекция американского картографа Гринтена. В ней весь земной шар изображается в одном круге.

В настоящее время при изыскании картографических проекций не пользуются вспомогательными поверхностями, а строят проекции аналитически. Названия же проекций с применением терминов вспомогательной поверхности позволяет понять их геометрическую суть.