Определить дирекционный угол ориентирного направления с помощьюгирокомпаса.
Определение дирекционного угла ориентирного направления по трем точкам реверсии с помощью гирокомпаса 1Г17определяется в такой последовательности:
1) Снять отчет по лимбу в момент первой точки реверсии N1и записать в бланк.
Чтобы не упустить момент точки реверсии, совмещения левых и правых штрихов изображения лимба рекомендуется начинать не позже чем за полминуты до наступления точки реверсии (с началом очень медленного движения лимба). Кроме того, для снятия отсчета можно воспользоваться кнопкой “ОТК. СЛЕД. СИСТЕМЫ” па пульте управления, нажать кнопку и отпустить. Когда отключится следящая система, лимб останется неподвижным.
Поворотом маховика оптического микрометра совместить штрихи левого и правого изображения лимба. Через 10 с питание следящей системы включается автоматически.
2) Снять отчет по лимбу в момент второй точки реверсии N2и записать в бланк. Наблюдения начинать не позднее чем через 3 мин после предыдущей точки реверсии.
3) Снять отчет по лимбу в момент третьей точки реверсии N3и записать в бланк.
4) Произвести вычисления:
– вычислить Nср1, Nср2, NсрΣ:
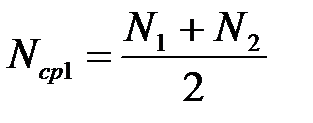 ; (4.4.1)
; (4.4.1)
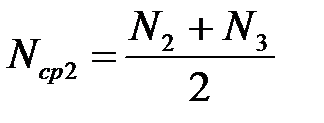 ; (4.4.2)
; (4.4.2)
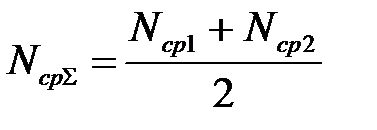 . (4.4.3)
. (4.4.3)
– вычислить истинный азимут Аист и дирекционный угол a:
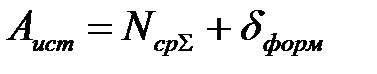 ; (4.4.4)
; (4.4.4)
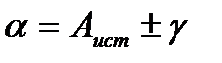 , (4.4.5)
, (4.4.5)
где dформ – формулярная поправка гирокомпаса; g – сближение меридианов (считывается с карты или определяется из специальных таблиц по прямоугольным координатам точки стояния гирокомпаса).
Если одна из точек реверсии переходит через 0°, то при вычислении Nср прибавляется 360° (60-00).
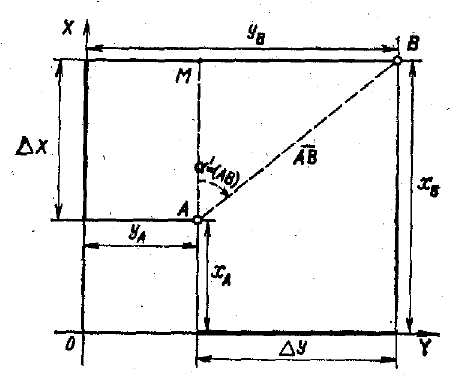
3.22 Решение ПГЗ: определить координаты точки В, по известнымкоординатам точки А хА; уА; расстоянию между точками А и В; идирекционному углу ориентирного направления (АВ).
Прямая геодезическая задача на плоскости заключается в нахождении координат определяемой точки по известным прямоугольным координатам заданной точки, расстоянию между ними и дирекционному углу с заданной точки на определяемую.
На рис. 3 показаны известные координаты точки А (хА, уА) и определяемые координаты точки В (хВ, уВ).
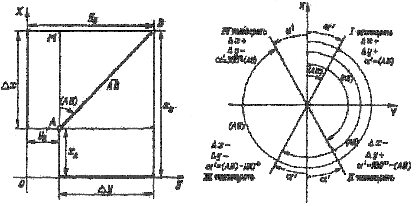
| Рис. 3. Прямая геодезическая задача |
| Рис. 4. Переход от дирекционного угла направления к углу 1 четверти |
Обозначим проекции прямой АВ на оси координат соответственно черезΔх и Δу.Тогда
хВ = хА + Δх;
уВ = уА + Δу.
Величины Δх и Δу называются приращениями координат. Их значения находим из прямоугольного треугольника АМВ:
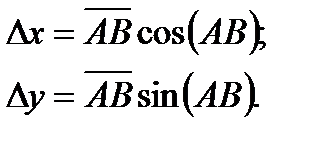 (1)
(1)
Сложив алгебраически приращения координат с координатами точки А, получим координаты точки В:
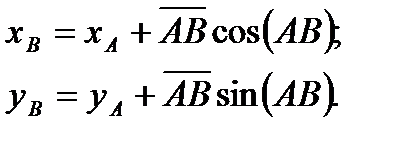 (2)
(2)
Формулы (2) представляют собой математическое выражение прямой геодезической задачи.
В зависимости от расположения определяемой точки относительно заданной, направление между ними может находиться в различных четвертях окружности (рис. 4). Для того чтобы в процессе вычисления приращений координат было удобно пользоваться таблицами логарифмов (натуральных значений) тригонометрических функций, которые, как правило, составлены для острых углов первой четверти, необходимо от дирекционного угла направления с заданной точки на определяемую перейти к значению угла первой четверти 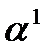 . При этом в целях сохранения наименования функций этот переход следует осуществлять от вертикального диаметра. На рис. 4 для направлении в различных четвертях записаны формулы перехода от дирекционного угла к углу первой четверти (острому углу). Знаки приращений координат зависят от знаков функций косинуса и синуса дирекционного угла направления, по которому вычисляется приращение координат (для наглядности они показаны на рис. 4).
. При этом в целях сохранения наименования функций этот переход следует осуществлять от вертикального диаметра. На рис. 4 для направлении в различных четвертях записаны формулы перехода от дирекционного угла к углу первой четверти (острому углу). Знаки приращений координат зависят от знаков функций косинуса и синуса дирекционного угла направления, по которому вычисляется приращение координат (для наглядности они показаны на рис. 4).
При решении прямой геодезической задачи можно также пользоваться таблицей 1.
Таблица 1
| Значение дирекционного угла направления | Четверть окружности | Знаки приращений координат | Формула для перехода от дирекционного угла к значению угла в первой четверти окружности | Знаки тригонометрических функций для направлений в различных четвертях | |
| Δх | Δу | ||||
| От 0 до 90˚ (от 0 до 15-00) От 90 до 180˚ (от 15-00 до 30-00) От 180 до 270˚ (от 30-00 до 45-00) От 270 до 360˚ (от 45-00 до 60-00) | I II III IV | + - - + | + + - - | α′ = (АВ) α′ = 180° - (АВ) α′ = (АВ) - 180° α′ = 360° - (АВ) | 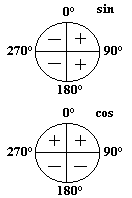 |
Приращения координат Δх и Δу при решении прямой геодезической задачи можно определять различными способами: по четырех- или пятизначным таблицам логарифмов; с помощью логарифмической линейки; по таблицам приращений координат; по номограмме инструментального хода (НИХ).
При вычислении приращений координат с помощью таблиц логарифмов используют формулы, которые получают в результате логарифмирования выражений (1), т. е.:
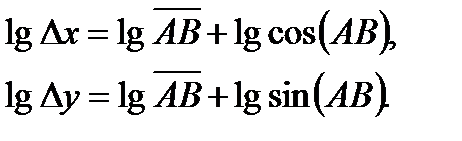 (3)
(3)
3.23Решение ОГЗ, вычислить дирекционный угол направления (АВ) ирасстояние АВ по координатам точек А и В. Рис. 5. Обратная геодезическая задача
Обратная геодезическая задача на плоскости заключается в нахождении дирекционного угла направления с одной точки на другую и расстояния между ними по прямоугольным координатам данных точек.
Из рис. 5 видно, что катеты прямоугольного треугольника АМВ равны:
АМ = Δх = хВ – хА;
МВ = Δу = уВ – уА.
Из прямоугольного треугольника АМВ находим:
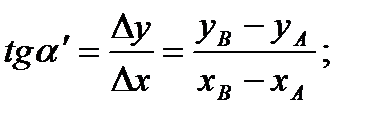 (4)
(4)
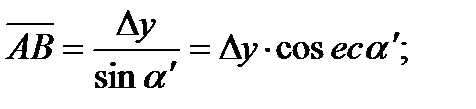 (5)
(5)
или
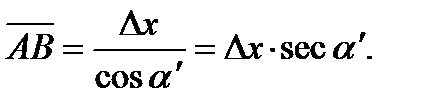 (6)
(6)
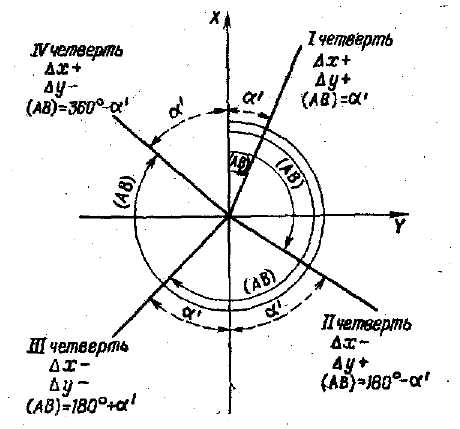
| Рис. 6. Переход от угла 1 четверти к дирекционному углу направления |
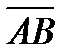 . За окончательное значение расстояния
. За окончательное значение расстояния 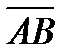 принимается величина, полученная по большей разности координат.
принимается величина, полученная по большей разности координат. При вычислении расстояния 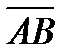 формула (5) применяется при α'>45° (7-50), а формула (6), когда α'<45° (7-50).
формула (5) применяется при α'>45° (7-50), а формула (6), когда α'<45° (7-50).
По значению тангенса угла α', вычисленному по формуле (4), в общем случае выбирается из таблиц не дирекционный угол направления (АВ), а острый угол α'. Для перехода к дирекционному углу пользуются зависимостями, которые даны на рис. 6. На этом же рисунке показан порядок определения четверти по знакам разностей координат.
Решение обратной геодезической задачи производится теми же способами, что и прямой геодезической задачи.
Для решения обратной геодезической задачи по таблицам логарифмов используют формулы, которые получают в результате логарифмирования выражений (4, 5 и 6), а именно:
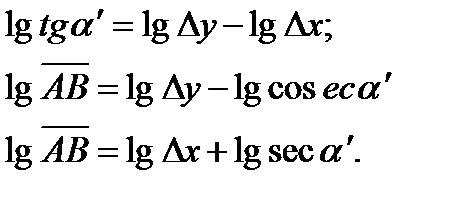 или (7)
или (7)
