Силы, формирующие течения. Классификация морских течений

Течения в океане возбуждаются и существуют под действием двух сил: трения ветра и силы горизонтального градиента давления, соответственно и течения разделяются на дрейфовые, или фрикционные, и градиентные, или гравитационные.

Причин же, порождающих течения, может быть несколько: ветер, разность плотностей воды, разность уровней, созданная атмосферным воздействием или притоком воды из рек, и др. Эти факторы приводят воду моря в движение, которое приобретает поступательный характер. Если причины, вызывающие поступательное движение воды, действуют кратковременно, то перенос невелик, и течения имеют эпизодический, кратковременный срок существования — это случайное течение. Если же определяющий фактор действует длительно, устойчиво, то образуется так называемое постоянное течение, линейный масштаб которого порядка 1000 км. Именно такие течения обеспечивают обмен вод, теплоты и солей между различными частями Мирового океана.

На течения влияют не только силы, вызвавшие их, но и силы вторичные, проявляющиеся вместе с возникновением течения: сила внутреннего трения (вязкость) и сила Кориолиса. Эти силы сами течения не вызывают, но они влияют на существующее течение. Сила трения на границах течения тормозит его, поглощая часть кинетической энергии потока, а сила Кориолиса вынуждает воду отклоняться от своего направления в Северном полушарии вправо, в Южном — влево.

Лучше всего разработаны две теории течений: теория Экмана, связанная с фрикционными течениями, и теория Бьеркнеса, связанная с плотностными течениями.

Теория ветровых течений

В основе любой теории течений лежат системы уравнений гидродинамики для компонентов вектора скорости, которые в каждом конкретном случае упрощаются в соответствии с задачей. В. Экман использовал два уравнения для компонентов вектора скорости и и v — проекций течения на оси х и у, учитывающие только две силы, уравновешивающие одна другую: силу трения, вызванного ветром на поверхности, и силу Кориолиса.

Задача была поставлена Ф. Нансеном, который во время экспедиции на «Фраме» (1893—1896) заметил отклонение дрейфа льда вправо от ветра, объяснил его воздействием силы Кориолиса и просил проверить это математическим решением. Первое решение было выполнено В. Экманом в 1902 г. и соответствовало наиболее простым и вместе с тем общим условиям: океан однороден по уровню, плотности и вязкости, бесконечно глубок, безбрежен и подвержен действию постоянного ветра (взятого по оси у). Ветер тоже безграничен и постоянен, движение установившееся (стационарное). В этих условиях решение имело вид:

и = V₀ e^-az cos (45° - az);

(10.24)

v= V₀ e^-аz sin (45° - az),

где v₀ — скорость течения на поверхности океана; а = , m — динамический коэффициент вязкости; r — плотность воды; w — угловая скорость вращения Земли; j — широта места, ось z направлена вниз.

Уравнения показывают, что течение на поверхности отклоняется от направления ветра на 45° вправо в Северном полушарии и влево — в Южном. Под поверхностью течение с глубиной уменьшается по абсолютной величине по экспоненциальному закону и продолжает отклоняться вправо в Северном полушарии, влево — в Южном. Проекция на поверхность океана пространственной кривой, проходящей через концы векторов скорости (огибающая), выразится логарифмической спиралью — спиралью Экмана (рис. 10.16).

На горизонте z=p/a течение имеет направление, противоположное поверхностному, а скорость равна 1/23 (около 4%) поверхностной, т. е. скорость практически затухает (следует вспомнить такую же закономерность и при волнении). Этот горизонт z=D, называемый глубиной трения, был определен Экманом по формуле

D= 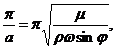(10.25)

а весь слой называется экмановским, или слоем трения.

Глубина трения, таким образом, зависит от широты места. Эта глубина изменяется от минимального значения на полюсе до максимального (бесконечности) на экваторе, где синус широты равен нулю. Это значит, что по теории ветровое течение на экваторе должно распространяться до дна, чего в природе нет. Толщина слоя ветрового течения практически ограничивается несколькими десятками метров.

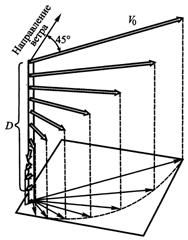
Рис. 10.16. Схема структуры ветрового течения (по В. Экману)

Остается определить, куда же переносится вода всего слоя, если течения на разных горизонтах имеют разные направления. Найти ответ можно, проинтегрировав по вертикали компоненты скорости течения. Оказалось, что перенос воды в ветровом течении, по Экману, происходит не по ветру, а перпендикулярно ему, вдоль оси абсцисс х. Это легко понять, так как в основе теории лежит предположение о равновесии силы трения (она направлена по оси ординат в положительном направлении) и силы Кориолиса. Зна­чит, последняя должна быть направлена по оси ординат в сторону отрицательных значений, а для этого перенос массы должен быть направлен по оси абсцисс в положительную сторону (для Северного полушария вправо).

Теория Экмана позволяет также получить формулу связи между скоростями ветра W и течения на поверхности V₀:

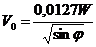. (10.26)

В формуле (10.26) коэффициент пропорциональности при скорости ветра W (0,0127) называется ветровым коэффициентом.

Потом Экман (1905) применил свою теорию к морю конечной глубины. При этом оказалось, что решение зависит от главного аргумента H/D — отношения глубины места к глубине трения. От него зависят и скорость ветрового течения, и угол отклонения течения от ветра, и форма кривой, огибающей векторы течения. При H/D=0,25 угол отклонения течения на поверхности равен 21,5°, при H/D=0,1 угол меньше 5°, вглубь от поверхности направление изменяется мало, а при H/D<0,1 направление течения во всем слое одинаково. Значение скорости у дна обращается в нуль.

Вблизи берега структура ветрового течения усложняется. В идеальном случае, когда берег представляет собой вертикальную стенку глубиной больше 2D и дно подходит к этой стенке перпендикулярно, образуется трехслойная система течений. Верхний слой глубиной D имеет нормально развитую структуру спирали Экмана, под ним лежит слой с неизменной по вертикали скоростью течения, направленной вдоль берега, — это градиентное течение. В слое, расположенном вверх от дна на расстоянии D (нижний слой трения), скорость течения уменьшается и изменяет направление по такой же спирали от значения скорости промежуточного слоя до нуля у самого дна. Схема такой структуры прибрежного течения показана на рис 10.17. Она иллюстрирует прибрежную циркуляцию вод при сгонном ветре, когда результирующий поток воды направлен от берега. Ветер при этом направлен так, что берег лежит с левой стороны (схема дана для Северного полушария). При противоположном ветре получается аналогичная схема для случая нагона, а ветер, перпендикулярный берегу, не будет давать ни сгона, ни нагона. Это нейтральный ветер. Такая схема в чистом виде не встречается, хотя у приглубых берегов (например, у Кавказского и Крымского берегов Черного моря) может наблюдаться сходная ситуация, приводящая в случае сгона к апвеллингу (см. 10.5.2).

У отмелых берегов, где H/D<0,25, наибольший сгонно-нагонный эффект создают ветры направлением, перпендикулярным к линии берега (например, в Финском и Таганрогском заливах), а его направление, параллельное линии берега, будет нейтральным.

На основе теории Экмана развивались и продолжают развиваться исследования ветровых течений. Например, были разработаны теории ветровых течений для мелкого моря различных форм. Определена роль ветровых изменений уровня в формировании схемы течений вод Мирового океана. Выяснилось, что под влиянием неравномерного ветра возникают наклоны водной поверхности, которые первое время мало изменяют поле плотности. Если ветер дует продолжительное время, то поле плотности перестраивается. Менее плотная вода верхних слоев под действием силы Кориолиса и ветрового нагона отходит в сторону высокого уровня (правая сторона течения в Северном полушарии), а более плотная вода на глубине оттекает в сторону меньшего уровня и давления (левая сторона течения).

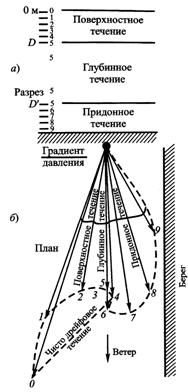
Рис. 10.17. Схема структуры течения у приглубого берега в разрезе (а) и плане (б)

(по В. Экману)

Плотностные течения

Плотностное течение порождает неравномерность распределения плотности в океане. Как было показано в разд. 10.6 (см. рис. 10.2), в низких широтах Мирового океана плотность воды на поверхности меньше, а удельный объем больше, чем в полярных областях. Следовательно, уровень во внутритропической области выше, чем в высоких широтах. Это приводит к движению воды по уклону, т. е. от тропиков к полюсам. Одновременно начинают действовать силы трения и Кориолиса, влияют очертания берегов, рельеф дна и еще накладывается глобальная система ветров. Все это вместе взятое и формирует общую циркуляцию вод океана.

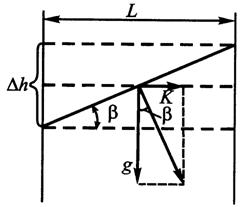
Рис. 10.18. Схема расчета наклона водной поверхности в океане; течение направлено «в чертеж»; Северное полушарие

Рассмотрим роль различия плотностей в формировании течений. На рис. 10.18 показано сечение равномерного потока в Северном полушарии, который идет «в чертеж». На каждую единичную массу на поверхности потока действуют силы тяжести g и Кориолиса К (для единичной массы ограничимся ускорениями), поэтому поверхность наклонена так, что она перпендикулярна равнодействующей обеих сил. Угол наклона определяют по формуле

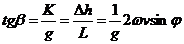. (10.27)

Отсюда находим скорость потока:

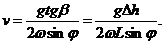(10.28)

Измерить превышение ∆h на поверхности моря достаточно точно нельзя, но можно найти его приближенно, если воспользоваться динамическим методом, предложенным в начале прошлого века В. Бьеркнесом применительно к атмосфере. В. Сандстрем и В. Хелланд-Хансен видоизменили его для океана. Широкому распространению динамического метода способствовали работы Н.Н. Зубова, который расширил его смысл и предложил очень простой метод расчетов. В этом методе используются единицы работы силы тяжести — геопотенциала (динамический дециметр): работа, затрачиваемая при поднятии массы в одну тонну на высоту 1/9,8 м, т. е. приблизительно на один дециметр (в единицах СИ это равно 1 кДж). Соотношение между глубиной, измеренной в динамических D и в линейных h метрах, запишется так: D = 0,lgh. Глубину можно измерить и в единицах давления (10⁴ Па): p = 0,lgh/a,где a — удельный объем воды. Связь всех трех величин запишется так:

D=0,1gh=pa; p= 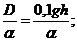h= 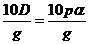. (10.29)

Это значит, что для воды соленостью 35‰и температурой 0 °С глубине один метр будет соответствовать работа 0,98 динамических метров и давление 1,01 децибара (101 гПа). Вообще числовые значения этих величин при любой температуре и солености будут различаться в пределах 3%. Это позволяет заменять числа, полученные в одних единицах, другими, просто переименовывая их: измеряя горизонты в линейных метрах, считать их полученными в децибарах.

Для определения скоростей течений в данном районе океана надо иметь достаточно плотную сеть станций и для каждой станции получить динамическую высоту, вычисляя ее вверх от некоторой отсчетной (нулевой) изобарической поверхности, принимаемой за начало отсчета для всех станций. Для океана часто берется изобара 1500 децибар, т. е. глубина 1500 м, так как это слой находится у нижней границы главного термоклина (для морей берется меньшее значение). Динамические высоты определяют по температуре и солености воды на каждом горизонте по формуле D=pa. Затем на карту наносят все значения высот в динамических сантиметрах (или миллиметрах) и проводят изолинии, называемые динамическими горизонталями. Теоретически они представляют собой линии тока, причем направление движения воды таково, что большая высота лежит в Северном полушарии справа по движению. Расстояние между изолиниями обратно пропорционально скорости течения, поэтому величина скорости может быть вычислена по разности динамических высот в двух точках, лежащих на расстоянии L одна от другой:

v= 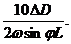(10.30)

Вследствие близости числовых значений динамических и линейных метров динамические карты показывают топографию поверхности моря. Динамические карты составлены для всех океанов и морей. Они дают генеральную картину стационарной геострофической циркуляции, в которой внутреннее трение пренебрежимо мало, а действующая сила — градиент давления — уравновешивается только силой Кориолиса. Пример динамической карты дан на рис. 10.19.

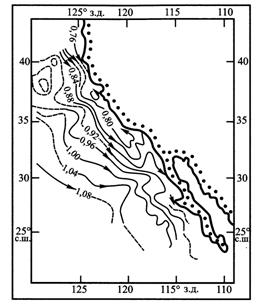
Рис. 10.19. Динамическая карта района Калифорнийского течения для июля (по Уайли). Динамические высоты (м) даны относительно отсчетной поверхности 500 м (5 • 10⁶ Па)

В настоящее время метод расчета значительно усовершенствован, модели течений позволяют решать полную систему уравнений гидродинамики, учитывающую воздействие ветра, влияние рельефа дна, трение о дно, переменную плотность воды, изменение силы Кориолиса с широтой и т.д. При этом единая отсчетная поверхность либо не требуется вовсе, либо расчет идет от уровня поверхности океана, полученного по балансу суммарных расходов течений или по данным спутниковой альтиметрии.