Работа 1 масштабы, их точность.

ИНЖЕНЕРНАЯ ГЕОДЕЗИЯ

Учебное пособие

для выполнения расчетно-графической работы

«Топографические карты и планы»

для студентов 1-го курса строительного факультета

специальностей 270102, 270105, 270106

Брянск, 2009

УКД 528.9 (072)

Учебное пособие для выполнения расчетно-графической работы «Топографические карты и планы» для студентов 1-го курса строительного факультета специальностей 270102, 270105, 270106

Составитель: доцент кафедры графики и геодезии,

кандидат сельскохозяйственных наук Т.В.Мащенко

– Брянск: БГИТА, 2009. - ___ с.

Пособие по разделу курса инженерной геодезии. Написано в соответствии с требованиями образовательного стандарта. Описаны теоретические сведения по разделу «Топографические карты и планы», «Рельеф земной поверхности и его изображение». Приводится задание к выполнению расчетно-графической работы по карте и методические указания по его выполнению.

Рецензенты:

зав. кафедрой «Строительные конструкции»,

профессор, к.т.н. С.Г. Парфенов

зав. кафедрой «Автомобильные дороги»,

доцент, к.т.н. З.А. Мевлидинов

зав. сектором геодезической службы

Главного управления развития территорий

Г. Брянска В.К. Милешин

Рекомендовано редакционно-издательской и методической комиссией строительного факультета БГИТА.

Протокол № от 2009 г.

Содержание

Введение…………………………………………………………..…….4

1 Теоретические сведения к работе 1………………………………….......5

2 Задание к работе 1…………………………...………………….............10

3 Теоретические сведения к работе 2………………………………….....12

4 Задание к работе 3…………………………...………………….............19

5 Теоретические сведения к работе 3………………………………….....26

6 Задание к работе 3…………………………...………………….............37

7 Теоретические сведения к работе 4………………………………….....38

8 Задание к работе 4…………………………...………………….............41

9 Приложение 1…………………………………………………………… 48

10 Приложение 2 (образец выполнения работы по карте)……………...56

12 Список использованной литературы ………………………………....67

Введение

Целью данной работы является изучение масштабов и их видов, получение навыков по измерению и откладыванию расстояний на картах и планах; изучение условных знаков и получение навыков в чтении карт и планов; решение задач на топографических картах и планах при проектировании различных сооружений. Эти задачи необходимо уметь решать инженеру-строителю в процессе проектирования сооружений различного вида, а также при расчетах инженерных сетей и вертикальной планировки площадок.

Данное пособие включает теоретические сведения, задания и методические указания к выполнению заданий по следующим работам:

Работа 1 Масштабы, их точность.

Работа 2 Решение задач по топографической карте без учета рельефа.

Работа 3 Решение задач по топографической карте с учетом рельефа.

Работа 4 Условные знаки планов и карт.

РАБОТА 1

Задание к работе 1. Масштабы, их точность

Задание 1.Оцифровать линейный масштаб с основанием а=1см для численного масштаба 1:

Задание 2.Изобразить на плане следующие длины отрезков:

Масштабы	Длина отрезка
на местности, м	на плане
1:200
1:500
1:1000
1:25000

Задание 3. Определить длины отрезков (м), взятых с планов следующих масштабов

Масштабы	Длина отрезка
на плане	на местности, м
1:500
1:2000
1:10000
1:50000

Задание 4.Определить графическую точность нижеперечисленных масштабов:

Масштаб	Точность, м	Масштаб	Точность, м
1:200		1:5000
1: 500		1:10000
1:1000		1:25000
1:2000		1:500000

Задание 5. Вычертить поперечный масштаб с основанием 2 см

РАБОТА 2

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ К РАБОТЕ 2

Определить дирекционный угол заданной линии

В топографии и геодезии, а также на топографических картах ориентирование производится по северу с учетом углов по ходу часовой стрелки, поэтому для сохранения знаков тригонометрических функций положение осей координат, принятое в математике, повернуто на 90˚.

Дирекционным углом называют горизонтальный угол, отсчитываемый по ходу часовой стрелки от северного направления линии, параллельной осевому меридиану, до направления данной линии. По абсолютному значению дирекционные углы измеряются от 0° до 360°. Вертикальные линии километровой сетки на топографической карте — прямые, параллельные осевому меридиану. Следовательно, для решения этой задачи нужно измерить транспортиром угол между северным направлением вертикальной линии километровой сетки и направлением линии, соединяющей заданные точки.

Задание к работе 2.

Решение задачи 1

Определить прямоугольные координаты заданных точек:

1. На схеме листа карты (рисунок 1):

а) показать (приближенно) две заданные точки или точки задаются преподавателем;

б) провести ближайшие к ним вертикальные и горизонтальные линии километровой сетки;

в) провести оцифровку этих линий;

г) показать для каждой из точек ΔΧ и ΔУ.

Рисунок 1. Схема листа карты

2. Определить по масштабу карты величины ΔΧ и ΔУ для каждой точки с помощью поперечного масштаба и вычислить прямоугольные координаты этих точек.

3. Определить действительную величину ординат точек (выделить номер зоны, вычесть 500 км).

Решение:

Прямоугольные координаты точки А:

Х_А=

У_А=

∆Х_А=

∆У_А=

Х_А=

У_А=

У_{А действ}=

Прямоугольные координаты точки В:

Х_В=

У_В=

∆Х_В=

∆У_В=

Х_В=

У_В=

У_{В действ}=

Решение задачи 2

Определить географические координаты двух заданных точек А и В:

1. На листе карты провести (карандашом) через определенную точку:

а) параллель (параллельно горизонтальной рамке карты или линии соединяющей концы одноименных минут или десятисекундных интервалов по широте);

б) меридиан (параллельно вертикальной рамке карты или линии соединяющей концы одноименных минут или десятисекундных интервалов по долготе).

2. Отсчитать по шкале минутной рамки карты:

а) на восточной или западной рамке карты — широту точки;

б) на северной или южной рамке карты — долготу точки.

3. На схеме листа карты (рисунок 2):

а) подписать широту и долготу углов листа карты;

б) провести через определяемую точку параллель и меридиан;

в) произвести оцифровку минут по широте и долготе (пересекаемых меридианом и параллелью точки).

j = широты

l = долготы

Рисунок 2 - Схема листа карты с минутной рамкой

Решение задачи 3

(Определись дирекционный угол заданной линии):

1. Измерить транспортиром на карте угол, составленный северным концом вертикальной линии километровой сетки и направлением определяемой линии (по ходу часовой стрелки) .

2. Показать на схеме листа карты (рисунок 1) этот угол и подписать его значение.

3. Для определения точного значения дирекционного угла линии нужно по ранее определенным (в задаче №1) прямоугольным координатам точек решить обратную задачу на координаты:

tg rАВ = tg aАВ= (У_В-У_А) / (Х_В-Х_А)=

rАВ =

αАВ =

Решение задачи 4

(Определить истинный и магнитный азимут той же линии):

1. Измерить транспортиром на карте угол, образованный северным концом истинного меридиана и направлением определяемой линии (по ходу часовой стрелки).

2. Показать этот угол на схеме листа карты и подписать его значение.

3. Произвести контроль правильности определения истинного азимута, т. е. вычислить его значение другим (аналитическим) способом по формуле:

А_ист = α + γ,

где γ – угол сближения меридианов, среднее значение которого указано в юго-западном углу листа карты.

4. Определить магнитный азимут линии, исходя из формулы:

А_маг = А _ист ± d,

где d - уклонение магнитной стрелки, среднее значение которого указано в юго-западном углу листа карты.

5. Составить схему решения этой задачи.

Решение:

Схема расположения меридианов на карте масштаба 1:……………..

d =

g =

А _ист=

А _магн=

РАБОТА 3

Основные формы рельефа.

В зависимости от характера рельефа местность делят на равнинную, холмистую и горную. Рельеф местности слагается из различных сочетаний форм земной поверхности, к основным из которых относятся холм, котловина, хребет, лощина и седловина.

Холм, гора – выпуклая, конусообразная форма рельефа, возвышающаяся над окружающей местностью (рис. 3)

Рисунок 3 - Холм

Наивысшая точка горы или холма называется вершиной.От вершины во все стороны идут скаты; линия перехода скатов в окружающую равнину называется подошвой. Гора отличается от холма размерами и крутизной скатов; при высоте над окружающей местностью до 200 м подобная форма рельефа с пологими скатами называется холмом, а более 200 м с крутыми скатами –горой. Горы и холмы изображаются замкнутыми горизонталями с бегштрихами, направленными от вершины к подошве.

Котловина или впадина– противоположная горе (холму) форма рельефа, представляющая чашеобразное углубление земной поверхности (рис. 4).

Рисунок 4 - Котловина или впадина

Самая низкая точка котловины называется дном. Боковая поверхность состоит из скатов; линия их перехода в окружающую местность называется бровкой. Котловина, как и гора, изображается замкнутыми горизонталями, однако бегштрихи в этом случае направлены ко дну.

Хребет – вытянутая и постепенно понижающаяся в одном направлении возвышенность (рис. 5).

Рисунок 5 - Хребет

Хребет обычно представляет собой ответвление от горы или холма. Линия, соединяющая самые высокие точки хребта, от которой в противоположные стороны отходят скаты, называется водоразделом. Хребет изображается выпуклыми горизонталями, направленными выпуклостью в сторону понижения местности.

Лощина– вытянутая или постепенно понижающаяся в одном направлении возвышенность (рис. 6).

Рисунок 6 - Лощина

Два ската лощины, сливаясь между собой в самой низкой ее части, образуют линию водослива или тальвег. Разновидностями лощины являются: долина – широкая лощина с поло­гими скатами; овраг – (в горной местности – ущелье) – узкая лощина с обрывистыми обнаженными скатами. Лощина изо­бражается вогнутыми горизонталями, направленными вогнутостью в сторону понижения местности; обрывистые склоны оврага изображаются специальными условными знаками (рис. 7).

Рисунок 7 - Овраг

Седловина – пониженный участок местности, расположенный на хребте между соседними вершинами (рис. 8).

Рисунок 8 - Седловина

От седловины берут начало две лощины, распространяющиеся в противоположных направлениях. В горной местности седловины служат путями сообщения между противоположными склонами хребта и называются перевалами. Седловина изображается горизонталями, обращенными выпуклостями навстречу друг к другу.

Вершина горы, дно котловины, самая низкая точка седловины и точки перегиба скатов называются характерными точ­ками рельефа, а линии водораздела и водослива – харак­терными линиями рельефа.

Все формы рельефа образуются из сочетания наклонных по­верхностей – скатов, которые подразделяются на ровные, вы­пуклые, вогнутые исмешанные (рис. 9).

ровный скат выпуклый скат вогнутый скат смешанный скат

Рисунок 9 - Формы скатов

Как видно из рисунка 9, горизонтали, изображающие ровный скат, располагаются на одинаковых расстояниях друг от друга. При выпуклом скате расстояния между горизонталями у подошвы меньше, чем у вершины. При вогнутом скате горизонтали у подошвы отстоят друг от друга на большем расстоянии, чем у вершин. Следовательно, по характеру горизонталей на топографиче­ской карте или плане можно установить форму скатов.

Свойства горизонталей

Из сущности изображения рельефа горизонталями вытекают следующие основные их свойства:

1. Все точки, лежащие на одной и той же горизонтали, имеют одинаковую высоту.

2. Замкнутые в пределах карты или плана горизонтали обозначают холм или котловину.

3. Горизонтали на плане или карте должны быть непрерывными линиями.

4. Горизонтали не могут пересекаться и разветвляться. Исключение может составлять случай, когда горизонталями изобра­жается нависший утес. Поэтому для изображения на картах скал (в том числе и нависших утесов) установлен специальный условный знак.

5. Расстояние между горизонталями в плане (заложение) характеризует крутизну ската, т. е. угол наклона ската к горизонту v.

Как следует из рисунка 10,б угол наклона v₁ линии местности АВ, которой соответствует заложение Аb, больше угла наклона v₂ линии АС, заложение которой Ас>Аb, следовательно, при данной высоте сечения рельефа h крутизна линии тем больше, чем меньше ее заложение.

Рисунок 10 - Крутизна ската (разрез)

Заложение (рис. 11), нормальное к горизонталям и являющееся кратчайшим, называется заложением ската. За­ложению Ab = d соответствует линия местности АВ наибольшей крутизны, называемая линией ската, которая принимается за направление ската в данной точке А.

Рисунок 11 - Крутизна ската (план)

Отношение высоты сечений рельефа к заложению называется уклоном линии:

Уклоны линии выражаются в процентах либо промилле (ты­сячных долях единицы).

Например: h=1 м, d=40 м. Тогда i =1м / 40 м = 0,025= 25 ⁰/₀₀ = 2,5%.

Определив уклон линии местности, легко найти крутизну ската по данному направлению из выражения

v=arctg

6. Линии водоразделов и водосливов пересекаются горизон­талями под прямыми углами (рис.5, 6).

7. Горизонтали имеют отметки, кратные высоте сечения рельефа. Например, при высоте сечения рельефа h=1 м горизонтали будут иметь отметки 120; 121; 122; 123 м и т. д.; при h = 2,5 м - 120; 122,5; 127,5; 130 м и т. д.

При чтении карты или плана, а также при их составлении следует помнить, что все горизонтали, бергштрихи, подписи вы­сот и другие условные знаки, относящиеся к рельефу, изобража­ются коричневой тушью (сиеной жженой).

3.1.3 Проведение горизонталей по отметкам точек

В процессе топографической съемки на планшете получают плановое положение характерных точек рельефа местности с их отметками. На основании отметок этих точек изображается рельеф местности в горизонталях. Для этого, руководствуясь мас­штабами составляемого плана или карты и характером снимае­мой местности, в соответствии с требованиями инструкции выби­рают высоту сечения рельефа. Точки, лежащие на одном скате, соединяют прямыми линиями. Затем на каждой линии находят точки, отметки которых кратны высоте сечения рельефа; это дей­ствие называется интерполированием горизонталей.

Интерполирование горизонталей может выполняться «на глаз» либо графически. Интерполирование «на глаз» допуска­ется производить в процессе съемки при наличии у исполнителя соответствующих профессиональных навыков. Сущность графи­ческого интерполирования состоит в следующем.

Пусть на линии 1-2 (рис. 12), отметки точек которой 1 и 2равны, соответственно, 48,7 м и 51,2 м, требуется найти поло­жение точек с отметками, кратными выбранной высоте сечения рельефа h = 1 м, т. е. 49, 50 и 51 м.

а б в

Рисунок 12 - Графическое интерполирование горизонталей:

а - с помощью миллиметровки; б, в - с помощью палетки

На листе миллиметровой бумаги через одинаковое расстояние (например, 0,5 или 1,0 см) проводят ряд параллельных линий, которые оцифровываются согласно отметкам точек и принятому сечению рельефа.

Приложив лист миллиметровки к линии 1-2, сносят точки 1и 2согласно их отметкам на миллиметровку. Соединив полученные точки 1 и 2прямой линией, получим профиль по линии 1-2. Отмечают точки пересечения линии 1' - 2' профиля с оцифрованными линиями миллиметровки (точки а, b, с). Спроектировав эти точки на линию 1-2, получают положение точек, через которые должны проходить горизонтали с отметками 49, 50 и 51 см.

В практике вместо миллиметровки для графического интерполирования часто используют палетку – восковку (кальку) с рядом параллельных линий, проведенных через равные проме­жутки (например, через 0,5 см). Линии оцифровывают согласно выбранной высоте сечения рельефа и отметкам точек плана, между которыми производится интерполирование. Накладывают палетку, например, на линию 3-4(рис. 12) так, чтобы точка 3оказалась на соответствующей отметке палетки. Затем, прижав палетку в точке 3иглой, вращают палетку вокруг этой точки до тех пор, пока точка 4 не окажется на соответствующей отметке палетки (рис. 12). Точки пересечения линии 3 - 4линиями па­летки перекалывают на план и у каждой из точек подписывают соответствующую отметку. Аналогично производят интерполиро­вание всех других линий. Затем точки на плане с одинаковыми отметками соединяют плавными кривыми линиями и получают изображение рельефа горизонталями.

3.1.4 Определить отметку точки А, лежащей на горизонтали

Отметка точки, лежащей на горизонтали, равна отметке этой горизонтали. Следовательно, задача сводится к определению отметки горизонтали, на которой лежит заданная точка (рисунок 3). Если отметка горизонтали не подписана, определяется высота сечения рельефа как частное от деления разности двух подписанных горизонталей на число промежутков
между ними.

Рисунок 13 - Определение отметки точки, лежащей на горизонтали

h = (170, 0 – 160, 0) / 4 = 2, 5 м

Затем, по надписям горизонталей и бергштрихам определяется направление ската. Отметка точки равна отметке подписанной горизонтали плюс или минус высота сечения, умноженная на число промежутков.

H_A = 160,0 м + 2,5м = 162,5 м

3.1.5 Определить отметку точки В, лежащей между горизонталями

Через заданную точку (рисунок 14) нужно провести вспомогательную линию, пересекающую горизонтали под прямым углом. Измеряют длину этой линии l_mn и расстояние от точки В до ближайшей горизонтали l_bn. Отметка точки определится, если к отметке горизонтали прибавить превышение h, вычисляемое из пропорции:

h'/h = l_МB/ l_MN,

откуда h' = (h · l_МВ) : l_MN,

где h – высота сечений горизонталей;

l_MN – длина проведенной вспомогательной линии;

l_BN – расстояние от точки до ближайшей наименьшей горизонтали;

Рисунок 14 - Определение отметки точки, лежащей между горизонталями

l_MN = 8 мм; l_BN = 7 мм; h = 2,5 м;

h´ = (h ·l_МB)/ l_MN = (2,5 · 7)/15 = 1,16 м;

H_В = 177,5м – 1,16 м= 176,34м.

Данные расчеты сделаны с учетом масштаба изображения.

Задание к работе 3.

РАБОТА 4

Решение задачи 1.

Определить прямоугольные координаты заданных точек:

1. На схеме листа карты (рисунок 1):

а) показать (приближенно) две заданные точки или точки задаются
преподавателем;

б) провести ближайшие к ним вертикальные и горизонтальные линии
километровой сетки;

в) провести оцифровку этих линий;

г) показать для каждой из точек ΔХ и ΔУ.

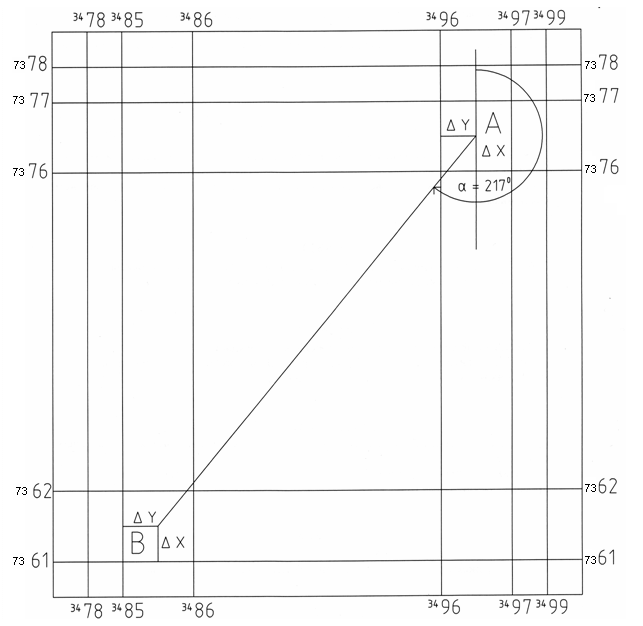Рисунок 1 - Схема листа карты

2. Определить по масштабу карты величины ΔХ и ΔУ для каждой точки с помощью поперечного масштаба и вычислить прямоугольные координаты этих точек.

3. Определить действительную величину ординат точек (выделить номер зоны, вычесть 500 км).

Решение:

Для точки А:

Х_А = 7376 + ΔХ_а

Y_А = 3496 + ΔY_А

ΔХ_а = 0,55 (км)

ΔY_А = 0,8 (км)

Х_а= 7376 + 0,55 = 7376, 55 (км)

Y_А = 3496 + 0,8 = 3496,8 (км)

Y_B действ = 496,8 - 500 = -3,2 т. А смещена к западу на 3,2 км и находится в 3 зоне.

Для точки В:

X_B = 7361 + ΔX_B

Y_B = 3485 + ΔY_B

ΔX_B = 0,55 (км)

ΔY_B = 0,25 (км)

X_B = 7361 + 0,55 = 7361, 55 (км)

Y_B = 3485 + 0,25 = 3485, 25 (км)

Y_B действ = 485, 25 – 500 = - 14,75 т. В смещена к западу на 14,75 км и находится в 3 зоне.

Решение задачи 2.

Определить географические координаты двух заданных точек А и В:

1. На листе карты провести (карандашом) через определенную точку:

а) параллель (параллельно горизонтальной рамке карты или линии соединяющей концы одноименных минут или десятисекундных интервалов по широте);

б) меридиан (параллельно вертикальной рамке карты или линии соединяющей концы одноименных минут или десятисекундных интервалов по долготе).

2. Отсчитать по шкале минутной рамки карты:

а) на восточной или западной рамке карты — широту точки;

б) на северной или южной рамке карты — долготу точки.

3. На схеме листа карты (рисунок 2):

а) подписать широту и долготу углов листа карты;

б) провести через определяемую точку параллель и меридиан;

в) произвести оцифровку минут по широте и долготе (пересекаемых
меридианом и параллелью точки).

φ_А = 66º 30' - 1' 10'' = 66º 28' 50'' с. ш. φ_B = 66º 30' + 0º 3' 40'' = 66º 23' 40'' с. ш.

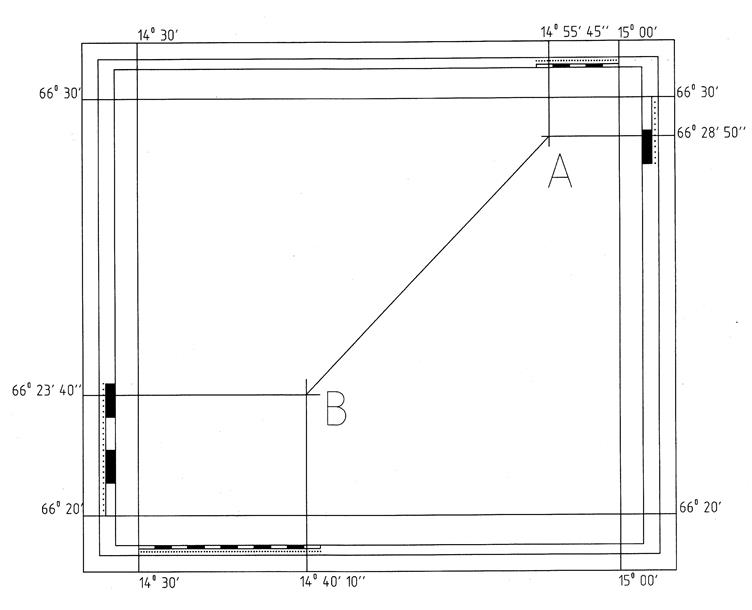λ_А= 15º 00' - 0º 4' 15'' = 14º 55' 45'' в. д. λ_B = 14º 30' + 0º 10' 10'' = 14º 40' 10'' в. д.

Рисунок 2 - Схема листа карты с минутной рамкой

Решение задачи 3

(Определись дирекционный угол заданной линии):

1. Измерить транспортиром на карте угол, составленный северным концом вертикальной линии километровой сетки и направлением определяемой линии (по ходу часовой стрелки) .

2. Показать на схеме листа карты (рисунок 1) этот угол и подписать его значение.

3. Для определения точного значения дирекционного угла линии нужно по ранее определенным (в задаче №1) прямоугольным координатам точек решить обратную задачу на координаты:

tg r_ав = tg α_ав = (Y_В-Y_А) / (Х_В-Х_А) = (3485, 25 - 3496, 8) / (7361, 55 - 7376, 55) = 0,7700

r_ав = ЮЗ:37º 35'

α_ав =180º + 37º 35' = 217º 35'

Решение задачи 4

(Определить истинный и магнитный азимут той же линии):

1. Измерить транспортиром на карте угол, образованный северным концом истинного меридиана и направлением определяемой линии (по ходу часовой стрелки).

2. Показать этот угол на схеме листа карты и подписать его значение.

3. Произвести контроль правильности определения истинного азимута, т. е. вычислить его значение другим (аналитическим) способом по формуле:

А_ист = α + γ,

где у - угол сближения меридианов, среднее значение которого указано в юго-западном углу листа карты.

4. Определить магнитный азимут линии, исходя из формулы:

А_маг = А_ист + δ,

где δ - уклонение магнитной стрелки, среднее значение которого указано в юго-западном углу листа карты.

5. Составить схему решения этой задачи.

Решение:

Схема расположения меридианов на карте масштаба 1:50000

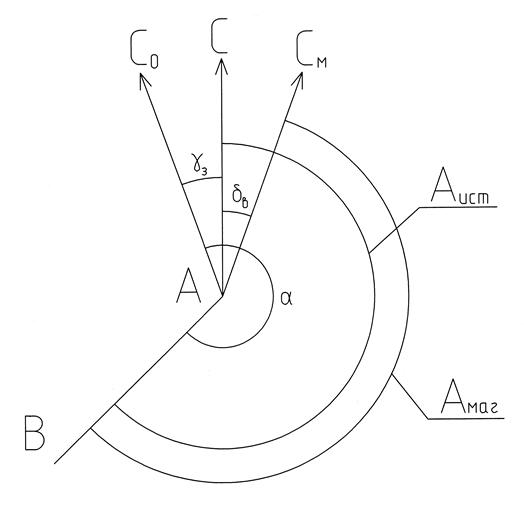δ_в = 8º 34'

γ_з = 0º 14'

А _ист = 217º 35' - 0º 14' = 217º 21'

А _маг = 217º 21' - 8º 34' = 208º 47'

Работа 3.

Работа 4.Условные знаки

№	Название и характеристика топографических объектов	Условные знаки топографических объектов для планов масштабов
1:5000 , 1:2000	1:1000 , 1:500
Масштабные
	1) Пустыри 2) Площадки строительные     Участки с изрытой поверхностью	1)	2)
Внемасштабные
	Мельницы ветряные каменные     Мельницы водяные
Пояснительные
	Плантации технических культур 1) травяных 2) древесных 3) кустарниковых	1) 2)   3)
	Линейные     Дороги по насыпям и дамбам.     Автомобильные с покрытием, откосы от края обочины Дороги в выемках

Список используемой литературы

1. Инженерная геодезия: Учебник для ВУЗов. Клюшин Е.Б., Киселев М.И., Михелев Д.Ш., Фельдман В.Д.; под редакцией Михелева Д.Ш. – 2-е изд., испр. – М., Высшая школа, 2001. – 463 с.

2. И.Ф. Куштин, В.И. Куштин. Инженерная геодезия. Учебник. Ростов-на-Дону: издательство ФЕНИКС, 2002. – 416 с.

3. Клюшин Е. Б., Михелев Д. Ш. Инженерная геодезия: Учебник для техникумов. – М.: Недра, 1990 – 264 с.: ил.

4. Поклад Г. Г. Геодезия. Учебник для ВУЗов. – М.: Недра, 1988. – 304с.

5. Фельдман В.Д., Михелев Д.Ш. Основы инженерной геодезии: Учебник. – 3-е изд., перераб. и доп. – М.: Высшая школа, издательский центр «Академия», 1999, – 300 с. ил.

6. Симонин С.И. Инженерно-топографическое черчение и наглядные изображения. Учебное пособие для вузов. Изд.2, перераб. И доп. М., Недра,1979. 192 стр.

7. Практикум по инженерной геодезии. Учебное пособие для вузов /Б.Б.Данилевич, В.Ф.Лукьянов, Б.С.Хейфец и др.: под ред. В.Е. Новака – 3-е изд. перераб. и доп. – М.: Недра, 1987, – 334 с.

8. Условные знаки для топографических планов масштабов 1:5000, 1:1000, 1:500. – М.: Недра, 1989, – 287 с.

9. Методические указания к лабораторным работам « Решение задач по топографической карте для студентов 1 курса», БТИ, 1980г.

Мащенко Татьяна Владимировна

Инженерная геодезия

Учебное пособие для выполнения расчетно-графической работы «Топографические карты и планы» для студентов 1-го курса строительного факультета специальностей 270102, 270105, 270106

Формат 60×94 1/16 Тираж 50 экз. 4,2 п.л.

Брянская государственная инженерно-технологическая академия.

241037. г. Брянск, пр. Станке Димитрова, 3,

Редакционно-издательский отдел.

Подразделение оперативной печати.

Подписано к печати __________2009 г.

ИНЖЕНЕРНАЯ ГЕОДЕЗИЯ

Учебное пособие

для выполнения расчетно-графической работы

«Топографические карты и планы»

для студентов 1-го курса строительного факультета

специальностей 270102, 270105, 270106

Брянск, 2009

УКД 528.9 (072)

Учебное пособие для выполнения расчетно-графической работы «Топографические карты и планы» для студентов 1-го курса строительного факультета специальностей 270102, 270105, 270106

Составитель: доцент кафедры графики и геодезии,

кандидат сельскохозяйственных наук Т.В.Мащенко

– Брянск: БГИТА, 2009. - ___ с.

Пособие по разделу курса инженерной геодезии. Написано в соответствии с требованиями образовательного стандарта. Описаны теоретические сведения по разделу «Топографические карты и планы», «Рельеф земной поверхности и его изображение». Приводится задание к выполнению расчетно-графической работы по карте и методические указания по его выполнению.

Рецензенты:

зав. кафедрой «Строительные конструкции»,

профессор, к.т.н. С.Г. Парфенов

зав. кафедрой «Автомобильные дороги»,

доцент, к.т.н. З.А. Мевлидинов

зав. сектором геодезической службы

Главного управления развития территорий

Г. Брянска В.К. Милешин

Рекомендовано редакционно-издательской и методической комиссией строительного факультета БГИТА.

Протокол № от 2009 г.

Содержание

Введение…………………………………………………………..…….4

1 Теоретические сведения к работе 1………………………………….......5

2 Задание к работе 1…………………………...………………….............10

3 Теоретические сведения к работе 2………………………………….....12

4 Задание к работе 3…………………………...………………….............19

5 Теоретические сведения к работе 3………………………………….....26

6 Задание к работе 3…………………………...………………….............37

7 Теоретические сведения к работе 4………………………………….....38

8 Задание к работе 4…………………………...………………….............41

9 Приложение 1…………………………………………………………… 48

10 Приложение 2 (образец выполнения работы по карте)……………...56

12 Список использованной литературы ………………………………....67

Введение

Целью данной работы является изучение масштабов и их видов, получение навыков по измерению и откладыванию расстояний на картах и планах; изучение условных знаков и получение навыков в чтении карт и планов; решение задач на топографических картах и планах при проектировании различных сооружений. Эти задачи необходимо уметь решать инженеру-строителю в процессе проектирования сооружений различного вида, а также при расчетах инженерных сетей и вертикальной планировки площадок.

Данное пособие включает теоретические сведения, задания и методические указания к выполнению заданий по следующим работам:

Работа 1 Масштабы, их точность.