Аналитическое интерполирование
Из подобия соответствующих треугольников получаем:
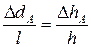 ;
; 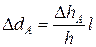 ;
; 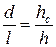 ;
; 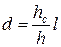 ;
; 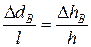 ;
; 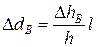 .
.
Пример 1. Пусть отметки точек A и В будут: HA = 12,3 м; HB = 15,6 м. Расстояние между точками на плане l = 56,0 м. Принятая высота сечения рельефа hc = 1 м (рис. 27).
Решение. Между точками А и В пройдут горизонтали с отметками 13; 14; 15 м. Местоположение крайних горизонталей определится отрезками
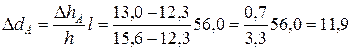 м,
м,
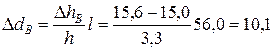 м.
м.
Отложив в масштабе плана от точки А отрезок 11,9 м и от точки В отрезок 10,1 м, получим местоположение горизонталей 13,0 и 15,0. Разделив расстояние между этими крайними горизонталями пополам, находим местоположение горизонтали 14,0.
Пример 2. Пусть при тех же исходных данных hc = 0,5 м. Тогда между точками А и В пройдут горизонтали 12,5; 13,0; 13,5; 14,0; 14,5; 15,0; 15,5. Соответственно
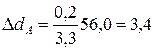 м;
м; 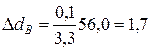 м.
м.
Разделив расстояние между крайними горизонталями на шесть частей, определим местоположение оставшихся пяти горизонталей.
Графическое интерполирование
Такое интерполирование, по сравнению с аналитическим, позволяет выполнить работу быстрее, с обеспечением необходимой точности. При графическом интерполировании используют интерполятор. Для построения интерполятора на кальке тушью вычерчивают ряд параллельных прямых линий на одинаковом расстоянии одна от другой (через 2, 4, 5 или 10 мм в зависимости от крутизны скатов данной местности и высоты сечения рельефа).
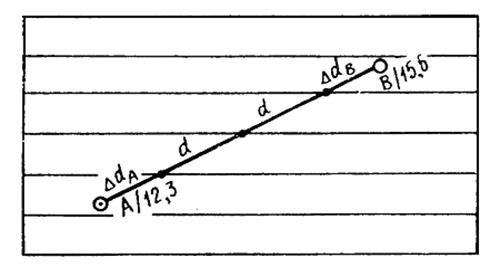
Рис. 27
Для определения местоположения горизонталей интерполятор накладывается так, чтобы число линий интерполятора между точками А и В (см. рис. 27) равнялось числу горизонталей на этом отрезке. Так, при исходных данных рассмотренного выше примера 1 отрезок АВ должны пересекать три линии интерполятора. Затем, поворачивая и смещая интерполятор, необходимо получить такое его положение, чтобы DdA составляло часть заложения d в соответствии с превышением DhA, и одновременно DdB также соответствовало превышению DhB. Оценка приведенных соответствий производится измерениями, при достаточном опыте – на глаз. Фиксировать на плане найденные точки местоположения горизонталей можно наколами иглы (обычно оказывается достаточным надавливание карандашом).
Интерполирование на глаз
При наличии достаточного опыта определение местоположения горизонталей производят на глаз, руководствуясь теми же положениями, которые приведены в аналитическом методе интерполяции. Практика показывает, что глазомерное интерполирование обычно обеспечивает точность в ¼ hc, что соответствует точности съемки рельефа.
Построение горизонталей заключается в соединении плавными кривыми точек, найденных в результате интерполяции (аналитической, графической или на глаз). Начинать целесообразно с характерных по рельефу форм местности. Водораздельные и водосливные линии пересекаются горизонталями под прямыми углами.
Практическая часть
1. В пределах квадрата километровой сетки по двум сторонам квадрата определите направление повышения и понижения местности, руководствуясь берг-штрихами, надписями горизонталей, отметками характерных точек на карте.
2. Нанесите характерные линии рельефа. Характерными линиями рельефа являются водораздельные и водосливные линии. В центральной части карты опознайте две смежные возвышенности, разделенные лощиной. В пределах квадрата километровой сетки построить водосливную линию и на участках возвышенностей, непосредственно примыкающих к лощине, постройте водораздельные линии. При построении водосливных и водораздельных линий имейте в виду, что они пересекают горизонтали в местах их наибольшей кривизны. Водораздельные линии проходят также через точки с наибольшими отметками и через средние точки седловины.
3. Определите отметки всех горизонталей в пределах заданного квадрата километровой сетки.
8. РЕШЕНИЕ ЗАДАЧ ПО ТОПОГРАФИЧЕСКИМ КАРТАМ
Определение отметок точек
При решении задач по определению отметок точек возможны следующие пять случаев.
1. Точка К (рис. 28) лежит на горизонтали. Ее отметка определится отметкой горизонтали (Hk = 79,0 м).
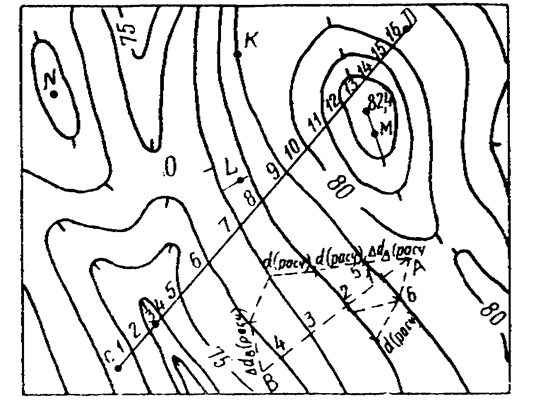
Рис. 28
2. Точка L находится между горизонталями с разными отметками. Проведя через точку L линию кратчайшего расстояния между горизонталями и применив линейную интерполяцию, определяем: HL = 77,6 м.
3. Точка М находится внутри замкнутой горизонтали и известна отметка характерной точки (вершины возвышенности) – 82,4. Проведя через точку с известной отметкой и точку М линию до горизонтали и применив линейную интерполяцию, находим: НМ = 82,2 м.
4. Точка N находится в центре замкнутой горизонтали, отметки характерной точки нет. В подобных случаях следуют правилу: превышение точки в центре замкнутой горизонтали принимается равным половине высоты сечения рельефа. Следовательно, в нашем случае
HN = 78,0 + 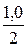 = 78,5 м.
= 78,5 м.
5. Точка О находится в точке седловины. Здесь также принимается превышение 0,5hc, тогда НO = 76,5 м.
Отметки точек по топографическому плану или карте вычисляют с точностью 0,1hc.
Определение крутизны ската
Крутизна ската оценивается посредством измерения угла наклона линии к горизонту n или величины уклона i, та и другая характеристика может быть или положительной, или отрицательной. Обе величины можно вычислить, применив формулу i = tgn = 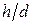 , или, для ускорения определения n и i, воспользоваться специальными графиками, которые называются масштабами заложений: масштабом заложений для уклонов (рис. 29, а); масштабом заложений для углов наклона (рис. 29, б).
, или, для ускорения определения n и i, воспользоваться специальными графиками, которые называются масштабами заложений: масштабом заложений для уклонов (рис. 29, а); масштабом заложений для углов наклона (рис. 29, б).
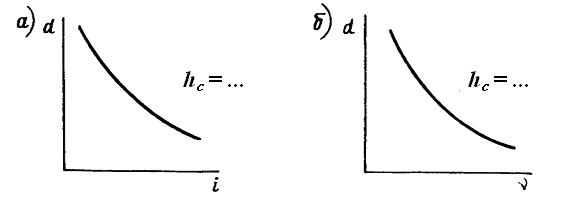
Рис. 29
Масштабы заложений строятся для определенной величины hc. Задаваясь различными значениями заложения горизонталей d (т. е. горизонтальное проложение между смежными горизонталями), можно вычислить угол n пo формуле tgn = 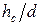 и уклон i =
и уклон i = 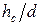 , затем построить масштабы заложений ni = f1(di)и ik = f2(dk).
, затем построить масштабы заложений ni = f1(di)и ik = f2(dk).
Для того чтобы по имеющимся масштабам заложений определить крутизну ската, следует в раствор циркуля взять заложение d,приложить к масштабу заложения так, чтобы одна ножка циркуля была на основании шкалы, а другая – на кривой, при этом обе ножки должны быть на перпендикуляре к основанию шкалы.
Уклон является безразмерной величиной, его можно также записать в процентах (%) или в промиллях (o/oo): i = 0,005 = 0,5 % = 5 o/oo .
