Форма земли и ее математическое выражение.

Форма земли и ее математическое выражение.

Мне до последнего времени было непонятно, почему существует так много разных систем. Если взять сколь угодно кривобокую землю и аккуратно порезать ее на дольки через полюса и Гринвич, а, затем от экватора на арбузные скибки, то почему она должна быть разная? Ну и пусть там, где она более выпуклая меридианы пройдут реже, чем в других местах. Просто карта этого места будет чуть-чуть шире. Это ведь не важно.

Ответ оказался прост - у нас до последнего времени не было ножика такого размера. Мы выражаем координаты в угловых градусах, а измеряем землю в километрах и метрах, вынужденные ползать по ее поверхности.При этом нам постоянно приходится пересчитывать метры в градусы и градусы в метры. Это не сложно, если знать и математически описать, какую форму имеет земля. Вот этим с переменным успехом и занимались ученые Земли, начиная с четвертого века до нашей эры.

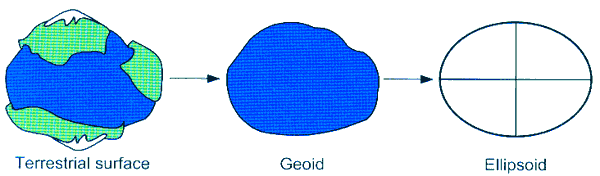
Опустим исторические перипетии этого процесса, и перейдем к временам не столь отдаленным. Наиболее точно известную форму земли называют "геоидом". Это не земля с горами и долинами, а воображаемая поверхность морей и океанов, если ее продолжить под материками. На такой земле в любой точке сила тяжести направлена строго перпендикулярно ее поверхности.

Геоид математически выражается с помощью коэффициентов сферических гармоник. Например, геоид Гравитационная модель Земли EGM 96, использует коэффициенты сферических гармоник для полиномов до 360 порядка. Для полного уравнения геоида EGM 96 требуется более 60 000 коэффициентов. Ясно, что использовать их все для расчета поверхности слишком сложно. Необходима более простая фигура, но с достаточной для нас точностью описывающая землю.

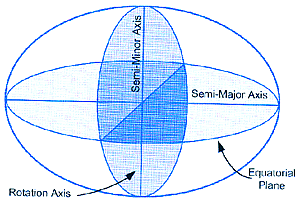Если считать землю шаром, то мы ошибемся как минимум на 22 километра. Если немного сплюснуть ее с полюсов и представить ее себе в виде эллипсоида вращения (двухосного эллипсоида), то ошибка уменьшится уже до 150-200 метров. Еще большей точности можно достичь, если еще немного сжать Землю с боков. Такая фигура называется трехосным эллипсоидом.

Существует и другой метод повышения точности - эллипсоид можно взять более простой (двухосный), но немного его сдвинуть и повернуть, чтобы он максимально соответствовал поверхности Земли в данной стране. Именно так обычно и делают.

Если опустить геодезические тонкости, то для нас датум - это размеры эллипсоида, принятого за основу в данной стране (так называемый опорный или референц эллипсоид) плюс коэффициенты, характеризующие его смещение и поворот, для совмещения с территорией данной страны.

Местные системы координат

Даже в самых точных геодезических измерениях постепенно накапливаются ошибки, достигающие в пределах такой страны как Россия нескольких метров. Для того, чтобы шмякнуть атомную бомбу на голову ненавистного врага такой точности хватит, а вот два огородника за полметра земли перегрызут друг-другу горло. Мэра провинциального городка расстояние от родного Мухосранска до ихнего Парижа интересует чисто теоретически, а вот влезет ли новый дом между двумя уже построенными и не придется ли перекапывать всю площадь в поисках газовой магистрали - вопросы вполне насущные.

Для составления очень крупномасштабных карт и планов, используемых в строительстве и землеустройстве, абсолютная точность не нужна, но вот расстояния между зданиями и сооружениями необходимы с сантиметровой точностью. В результате местные геодезисты "забивают" на государственную систему и все измерения проводят в своей собственной - локальной. Они в буквальном смысле забивают колышек в своем городе, считают его точкой отсчета и не имеют проблем до тех пор, пока не приходится строить мост через реку, разделяющую две области. Вот тут и возникает вопрос взаимоувязки местных систем координат, который решается долго и весьма болезненно.

Нулевые меридианы

Если у вас хватило терпения дочитать до этого места, то вы явно еще что-то помните из школьного курса географии. Вы точно знаете, что географическая широта отсчитывается от экватора и бывает северной и южной. Меридианы считаются на запад и на восток от нулевого меридиана или Гринвича, который находится в далекой Англии. Но Британия не всегда была владычицей морей и никогда не была лидером мировой астрономии и геодезии. Поэтому и нулевой меридиан вначале принадлежал не им.

Изначально все было гораздо правильнее и умнее. Чтобы не заморачиваться с восточной и западной долготой, нулевой меридиан поместили в самую западную точку старого света - остров Ферро (El Hierro) Канарского архипелага и привязали его к одинокому маяку на безлюдной скале. В результате вся Европа оказалась в восточном полушарии, а Америка в западном, что было очень удобно. Не удобно было то, что остров находился далеко в океане, и точно померить расстояние до него было в то время практически невозможно. Тогда было принято соломоново решение - договориться, что от Ферро до Парижа, где в то время была одна из самых современных обсерваторий, по широте ровно 20 градусов. После этого все меридианы измеряли от Парижа, а на картах писали от Ферро, добавив 20 градусов. Впоследствии оказалось, что этот маяк от Парижа находится на 29 минут или на 50 километров дальше, но это ничего не изменило.

В середине XIX века российские геодезисты Карл Теннер и Василий Струве очень точно померяли дугу земного меридиана, а Федор Шуберт, погрузив с собой несколько десятков высокоточных хронометров, отправился проверять меридианы. В результате были получены точные координаты нескольких сотен населенных пунктов по всей Европе, в том числе и точные координаты Пулковской обсерватории. С тех пор все измерения в России производили от Пулково, а координаты на картах писали вначале от Ферро, а затем от Пулково и Парижа, и только в начале двадцатого века на картах появился Гринвич.

Для того, чтобы пересчитать координаты на старых картах к современному Гринвичу к ним нужно добавить или из них вычесть соответствующую разницу. Эту величину лучше брать именно ту, которой она считалась во времена составления карты, например, из книги Шуберта "Expos des travaux astronomiques et geodesiques executes in russie":

От Ферро	Вычесть	17° 39' 50.60"
От Парижа	Добавить	02° 20' 09.40"
От Пулково	Добавить	30° 19' 40.11"

При этом надо не забывать, что от Пулково долгота тоже может быть восточной, и ее надо прибавлять к долготе Пулково, и западной, которую надо вычитать. Те, кто не помнят сколько минут в градусе или не в состоянии складывать в столбик десятично-шетидесятиричные числа, могут воспользоваться эксельной табличкой - LonCalc.xls.

Датумы нашей Родины.

Российская империя.

Карты, для которых имеет смысл говорить о датуме, появились в России в начале XIX века. Эти карты составлялись на основе весьма точной для того времени инструментальной съемки с использованием, наиболее соответствовавшего известной на тот момент форме земли, эллипсоида Бесселя 1841. На карты наносилась градусная сетка с долготой, указанной, для более поздних карт - от Пулково и Парижа, для более ранних - от Ферро. К слову сказать, известная в то время долгота острова Ферро весьма значительно отличалась от более точных значений, которые стали известны позднее.

Карты Менде. Генерал-майор А. И. Менде руководил топографическими съемками на большей части территории европейской России в течение 1848-1866 годов. При этом Тверская, Рязанская, Тамбовская и Владимирская губернии были закартографированы в масштабе 1 верста в 1 дюйме, Ярославская - 2 версты в 1 дюйме, Симбирская и Нижегородская - 3 версты в 1 дюйме, Пензенская - в масштабе 8 верст в 1 дюйме.
Отличительной чертой этих карт является то, что они выполнены в цвете. Долгота на них указана от острова Ферро.

Карты Шуберта. Генерал-лейтенант Федор Федорович Шуберт руководил топографическими работами в Росси с 1819 по 1843 год и, поэтому, все издаваемые в те годы карты имели к нему непосредственное отношение. Однако картами Шуберта принято считать только выпущенную в 1848 году на 6 листах топографическую карту окрестностей Москвы в масштабе 1 верста в дюйме,двухверстную карту Московской губернии 1860 года на 40 листах и, издававшуюся с 1821 по 1839 годы, Специальную карту Европейской России в масштабе 10 верст в дюйме, проекции Бонне и координатами от Ферро. Трехверстные карты России, изданные позднее, (с 1850 года), картами Шуберта считать нельзя.

При составлении своих карт, Шуберт не преследовал цель получить такую высокую точность, которая была характерна для триангуляций Теннера и Струве, руководивших в то время аналогичными работами в России. Основное внимание он уделял подробности и достоверности изображения на картах местных предметов.

Карты Стрельбицкого. В 1865 году под руководством Капитана Генерального Штаба Стрельбицкого, были начаты работы по переизданию, не отличавшихся высокой точностью, десятиверсток Шуберта. Новая Специальная карта Европейской России 10 верст в дюйме на 174 листах, уже в конической проекции Гаусса с координатами от Пулково и Парижа, была издана в 1971 году, дополнялась и переиздавалась вплоть до 1919 года.

Военная топографическая карта Российской империи в масштабе 3 версты в дюйме начала издаваться с 1850 года. Съемка, корректировка и издание дополнительных листов продолжалась до начала XX века. Эти карты достаточно подробны и охватывают наибольшую территорию.

Насколько точны дореволюционные карты? Оценить точность карт, не зная их датума и параметров проекции - невозможно. Использование их с несоответствующими параметрами датума и не в тех проекциях, приводит к ошибкам определения координат до нескольких километров. Для научных кругов эти карты представляют, по-видимому, только исторический интерес. Во всяком случае, научные работы, посвященные исследованию дореволюционных карт с точки зрения геодезии, мне неизвестны.

Привязка карт в программе OziExplorer с учетом параметров их проекций на эллипсоиде Бесселя с нулевыми параметрами преобразования выявили расхождения между изображением объектов на карте и их реальным положением на местности не более километра для карт Стрельбицкого и не более 400 метров для любой из трехверсток. Статистическая обработка координат нескольких десятков объектов на трехверстной карте Екатеринославской губернии 1888 года выявило разброс их значений в пределах 300 метров со смещением среднего значения порядка 200 метров, что позволило вычислить датум для этой карты - Bessel,3,606,151,407.

Выяснить, является ли это смещение отличием датума или это локальная его деформация в пределах отдельного региона, без обработки большого объема экспериментальных данных, собранных почти по всей территории восточной Европы, пока не представляется возможным.

Система СК-95

Появление спутниковой навигации позволило провести более точные измерения и проверить, считавшуюся до этого, весьма точной геодезическую сеть России. Оказалось что многие регионы изображены на картах с недопустимой ошибкой, а камчатка вообще "уехала" аж на 10 метров. В результате все было заново точно перемерено и уже не по нескольким десяткам, а по нескольким сотням пунктов и принята новая система координат СК-95, уже точно привязанная к ПЗ-90, а с ней вместе и к WGS-84 и кITRF.

Поскольку базовой точкой новой системы по-прежнему считается центр зала Пулковской обсерватории, то жители европейской России, Украины и Белоруссии могут не беспокоится. На их территории она не отличается от СК-42.

Когда появятся карты в новой системе неизвестно. Я думаю - никогда. Пока ее будут внедрять, весь мир перейдет на что ни будь всемирное, хоть на ту же WGS84.

СКУ 2000.

Первая собственная украинская система координат стала "жестким ответом злобным москалям" на принятие СК-95. Кроме громких заявлений в массовой печати я о ней ничего не нашел. Глубокое копание в Интернете утвердило меня в сугубо личном мнении, что за ней, кроме политических лозунгов да желания украинских ученых добиться хоть какого-то финансирования, ничего не стоит. Думаю, что судьба ее еще более печальна.

В результате все, что я здесь написал о системах координат, вы можете благополучно забыть. Для пользования спутниковой навигацией вполне достаточно одной WGS-84. Для работы с картами понадобится, имеющийся в любом навигаторе и в любой программе, датум Пулково 1942. И только черным копателям придется пошевелить мозгами и разобраться в пользовательских датумах и хитрых проекциях.

Форма земли и ее математическое выражение.

Мне до последнего времени было непонятно, почему существует так много разных систем. Если взять сколь угодно кривобокую землю и аккуратно порезать ее на дольки через полюса и Гринвич, а, затем от экватора на арбузные скибки, то почему она должна быть разная? Ну и пусть там, где она более выпуклая меридианы пройдут реже, чем в других местах. Просто карта этого места будет чуть-чуть шире. Это ведь не важно.

Ответ оказался прост - у нас до последнего времени не было ножика такого размера. Мы выражаем координаты в угловых градусах, а измеряем землю в километрах и метрах, вынужденные ползать по ее поверхности.При этом нам постоянно приходится пересчитывать метры в градусы и градусы в метры. Это не сложно, если знать и математически описать, какую форму имеет земля. Вот этим с переменным успехом и занимались ученые Земли, начиная с четвертого века до нашей эры.

Опустим исторические перипетии этого процесса, и перейдем к временам не столь отдаленным. Наиболее точно известную форму земли называют "геоидом". Это не земля с горами и долинами, а воображаемая поверхность морей и океанов, если ее продолжить под материками. На такой земле в любой точке сила тяжести направлена строго перпендикулярно ее поверхности.

Геоид математически выражается с помощью коэффициентов сферических гармоник. Например, геоид Гравитационная модель Земли EGM 96, использует коэффициенты сферических гармоник для полиномов до 360 порядка. Для полного уравнения геоида EGM 96 требуется более 60 000 коэффициентов. Ясно, что использовать их все для расчета поверхности слишком сложно. Необходима более простая фигура, но с достаточной для нас точностью описывающая землю.

Если считать землю шаром, то мы ошибемся как минимум на 22 километра. Если немного сплюснуть ее с полюсов и представить ее себе в виде эллипсоида вращения (двухосного эллипсоида), то ошибка уменьшится уже до 150-200 метров. Еще большей точности можно достичь, если еще немного сжать Землю с боков. Такая фигура называется трехосным эллипсоидом.

Существует и другой метод повышения точности - эллипсоид можно взять более простой (двухосный), но немного его сдвинуть и повернуть, чтобы он максимально соответствовал поверхности Земли в данной стране. Именно так обычно и делают.

Если опустить геодезические тонкости, то для нас датум - это размеры эллипсоида, принятого за основу в данной стране (так называемый опорный или референц эллипсоид) плюс коэффициенты, характеризующие его смещение и поворот, для совмещения с территорией данной страны.