Ориентирование на местности - определение своего положения на местности относительно сторон горизонта (стран света) с помощью компаса или карты

Ориентирование возможно по местным ориентирам (приметным объектам), по положению Солнца, Луны, звезд или с помощью (радио) сигналов.

Ориентирование линий.

Ориентировать линию - значит определить ее направление относительно истинного или магнитного меридиана. Направление истинного меридиана в данной точке определяется астрономически, магнитного -при помощи магнитной стрелки. Для ориентирования линий служат углы, которые называются азимутами, дирекционными углами и румбами.

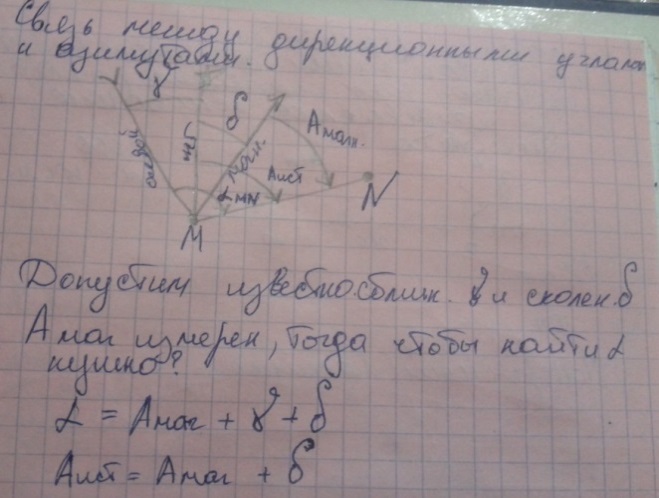
Азимут - горизонтальный угол, отсчитываемый от северного направления меридиана по ходу часовой стрелки до направления данной линии. Азимуты измеряются от 0 до 360°. Азимут называется истинным, если он отсчитывается от истинного меридиана, и магнитным, если отсчитывается от магнитного меридиана. Азимут одной и той же линии в разных ее точках различен.

Азимуты

Угол γв данной точке между ее меридианом и линией, параллельной осевому меридиану называется сближением меридианов. Сближение меридианов можно вычислить по приближенной формуле: γ=Δλsinφ

где, Δλ - разность долгот осевого и географического меридиана данной точки, φ-широта точки.

Дирекционный угол - горизонтальный угол, отсчитываемый от северного направления осевого меридиана или линии ему параллельной по ходу часовой стрелки до направления данной линии

Дирекционный угол одной и той же линии в разных ее точках одинаков, Дирекционный угол изменяется от 0 до 360. Между азимутами и дирекционными углами существует следующая связь

А = а±γ

Угол у имеет знак положительный, если точка Q на востоке от осевого меридиана, и отрицательный, если на западе.

Румб - острый горизонтальный угол, отсчитываемый от ближайшего направления меридиана до направления данной линии. Румб изменяется в пределах между 0 и 90° и сопровождается названием СВ, ЮВ, ЮЗ, СЗ.

Если румбы отсчитываются от истинного, магнитного или осевого меридиана, то их называют истинным магнитными или осевыми. Между азимутами и румбами существует связь

Азимуты Румбы

0-90° СВ: r₁=А₁

90-180° ЮВ: r₂=180-А₂

180-270° ЮЗ: r₃=А₃-180°

270-360° СЗ: r₄=360-А₄

2) Вычислительная обработка журнала технического нивелирования.

Камеральные работы при обработке результатов технического нивелирования выполняются обычно в следующей последовательности.

1. Проверка записей полевых отсчетов в журнале. Отсчеты должны быть записаны в виде четырехзначных цифр и соответствовать наименованию точки и ее положению на местности. Разность отсчетов по красной и черной сторонам рейки на связующих точках не должна отличаться от стандартной разности пяток рейки (4783 или 4683) не более +3 мм.

2. Вычисление превышений между связующими точками

hч = Зч - Пч,

hк = Зк - Пк.

Контролем работы на станции является hч - hк , +4 мм. Тогда, hср = (hч + hк)/2 с округлением по Гауссу до целых мм.

Например, 0546.5 округляют до 0546, а 0547.5 округляют до 0547мм.

3. Выполняют постраничный контроль

(ΣЗ - ΣП) / 2 = Σhср,

где ΣЗ и ΣП - суммы задних и передних отсчетов по рейке.

4. Уравнивают превышение в нивелирном журнале:

а) находят невязку fh = Σhср - (Нк - Нн);

б) оценивают невязку fh < fh доп.(30 мм √L);

в) вводят поправки бh =-fh/n;

г) выполняют контроль Σбh = -fh и Σhиспр.= Нк - Нн;

5. Вычисляют высоты связующих точек

Hi+1 = Hi + hиспр.

6. Для тех станций, где имеются промежуточные точки, определяют горизонт прибора, от которого вычисляют отсчет по рейке и получают ее высоту.

Нпр = ГП - ач,

ГП = Нпк1 + Зч,

ГП = Нпк2 + Пч.

3)

Билет 5

1)

Зональная система

Данная система координат применяется при горизонтальных съемках и составлении планов местности. Зональная система плоских прямоугольных координат. При топографических съемках, маркшейдерских и инженерно-геодезических работах более целенаправлено использовать системы плоских прямоугольных координат. Потому для изображения на плоскости значимых территорий земной поверхности используются картографические проекции, дающие возможность переносить точки с поверхности эллипсоида на плоскость по определенным математическим законам. В общем случае картографические проекции вызывают преломления как углов, так и длин. В геодезии выгодно использовать такие проекции эллипсоида на плоскость, которые не искажали бы углов. Подобные проекции именуются равноугольными либо конформными. Возникающие при этом преломления длин и площадей должны быть незначимыми и учитываться простыми формулами. При иных равных критериях преломления будут тем больше, чем обширнее участок поверхности эллипсоида, проектируемый на плоскость. Для того чтоб поправки за искажение длин были сравнимо невелики, при изображении огромных областей поверхности эллипсоида их делят на отдельные участки (зоны) и каждый из их изображается на плоскости в системе прямоугольных координат. Для развертки поверхности земного эллипсоида на плоскость без разрывов используют разные способы проектирования его на вспомогательные поверхности..

2) Тригонометрическое нивелирование – определение высот точек земной поверхности относительно исходной точки с помощью угла наклона визирного луча, проходящего через две точки местности,

Выполняют тригонометрическое нивелирование с помощью теодолита в точке А угол наклона  визирного луча, проходящего через визирную цель в точке В, и зная горизонтальное расстояние sмежду этими точками, высоту инструмента l и высоту цели а (рис. 2), разность высот h этих точек вычисляют по формуле:

h = stg + l - a.

Эта формула точна только для малых расстояний, когда можно не считаться с влиянием кривизны Земли и искривлением светового луча в атмосфере (см. Рефракция). Более полная формула имеет вид:

h = s tg + l - a + (1 - k) s²/2R,

где R – радиус Земли как шара и k–коэффициент рефракции.

Тригонометрическим нивелирование определяют высоты пунктов триангуляции и полигонометрии. Оно широко применяется в топографической съёмке. Тригонометрическое нивелирование позволяет определять разности высот двух значительно удалённых друг от друга пунктов, между которыми имеется оптическая видимость, но менее точно, чем геометрическое нивелирование Точность его результатов в основном зависит от трудно учитываемого влияния земной рефракции.

3)

Билет 6

1)

2) Линейные измерения - определение расстояний между задан­ными точками, определение размеров элементов разных сооружений, деталей (при необходимости измерение площадей, объемов) - применяются во многих областях науки и техники. Любое измерение состоит в установлении численного соотношения между величиной измеряемого объекта и величиной эталона, воспроизводящего единицу измерения.

. приборы для измерения длин линий, применяемые в настоящее время в инженерной геодезии, можно условно разделить на две большие группы: механические и физико-оптические.

Механические мерные приборы представляют собой линейные меры различной длины, изготавливаемые чаще всего из металла в виде лент, рулеток, проволок и т. п., служащие для непосредственного измерения длины линии путем последовательного отложения длины мерного прибора в створе измеряемой линии. Результат измерений получают суммированием количества отложений в принятых единицах измерений.

Измерения производят либо по поверхности земли, либо подвешивая мерный прибор на небольшой высоте (1—1,5 м) на специальных штативах. В обоих случаях вместо прямой — кратчайшего расстояния между конечными точками линии — измеряют некоторую ломаную линию. Поэтому для получения горизонтального положения измеряют углы наклона линии или отдельных ее частей.

Ленты землемерные (ГОСТ 10815—64). Отечественная промышленность выпускает землемерные ленты двух типов: ЛЗ — лента землемерная и ЛЗШ — лента землемерная штриховая. Их номинальная длина может быть 20, 24 и 50 м.

Рулетки измерительные металлические (ГОСТ 7502—69). Для измерений в строительстве наиболее удобны стальные рулетки типов: PC—рулетка самосвертывающаяся, РЖ — рулетка желобчатая, РЗ — рулетка в закрытом корпусе, РК — рулетка на крестовине, РВ — рулетка на вилке и РЛ — рулетка с грузом.

В зависимости от положения начала шкалы на измерительной ленте рулетки ГОСТ предусматривает выпуск рулеток в двух исполнениях: А — начало шкалы сдвинуто от торца измерительной ленты; Б — начало шкалы совпадает с торцом измерительной ленты.

По точности нанесения шкал рулетки могут изготовляться трех классов: 1-го и 2-го классов — в исполнении А; 3-го класса типов PC, РЗ, РК и РВ — в исполнениях А и Б, типа РЖ — в исполнении Б. Начало шкалы рулеток типа РЛ должно совпадать с нижним концом груза.

Рулетки в зависимости от класса точности и материала изготовления обеспечивают производство линейных измерений с относительными ошибками от 1 :2000 до 1 :20 ООО. При измерениях повышенной точности необходимы тщательное кооперирование рулетки, измерение и учет температуры, а также постоянство натяжения. Уравнение длины рулетки составляется в том же виде, что и для землемерных лент.

Рулетки с учетом их технических характеристик можно рекомендовать для различных геодезических работ в строительстве: измерение линий, разбивочные работы, поэтажное распространение отметок, исполнительные съемки, различные обмеры габаритов конструкций и др.

Достоинства рулеток и землемерных лент — простота устройства и эксплуатации при сравнительно высокой точности измерений, особенно коротких линий. Недостатки — большая трудоемкость при измерении длинных линий, необходимость расчистки наземной трассы, вешения, измерения углов наклона отдельных участков линий и т. д.

При измерении линий мерными лентами их укладывают по земле на ровной местности. При вешении линии с створе в землю забивают толщиной 4-6 см с интервалами, равными длине ленты. На торцах кольев наносят штрих крестик. Ленту укладывают на землю и берут отсчеты З и П. Длина пролета t=t0+П-З

Длину измеряют дважды в прямом и обратном направлении. расхождение не должно превышать 1/2000(при неблагоприятных условиях 1/1000).за окончательное значение принимают среднее.

3)

Билет 7

1)