Зональная система плоских прямоугольных координат

Они наиболее просты для отображения результатов решаемых геодезических задач методами аналитической геометрии на плоскости и упрощают математическую обработку результ. Измерений.

Государственная зональная система прямоугольных координат создана ( бывш. СССР) с применением конформной проекции Гаусса- Крюгера ( сохраняет подобие изображаемых фигур) Гаусс разработал теории а Крюгер разработал таблицы и формулы для вычислений 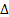координат точек сферойда на плоскости сферойда в гестиградусных зонах. Проекция явл. Поперечно цилиндрической когда картинная плоскость предствалена в виде цилиндра косающегося поверхности вдоль одного из меридианов см рис 1.5 а,б,в

Проекция Гаусса Крюгера принята левая система треугольных координат. В этой системе заложено условие комфортности согласно которому проекции малых величин сохраняют подобие, а осевой меридиан каждой зоны изображается на плоскости с постоянным масштабом m_o = 1 и принимается за ось абсцысс X с началом в точке O в пересечении с осью ординат У которая представляет изображение отрезка экватора (см. рис. 1.5 б) при этом масштаб проекции вдоль оси У получается переменным – увеличивается при удалении от оси Х . Направление от экватора оси Х северное и абсцысы все положительны.

Изображение восточной и западной частей зоны ординаты положительны а в западной отрицательны.

В средней широте Беларуси(приблизительно 53^о ) ширина в 6-и градусной зоны равнв l2yl 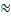2*200 для оценочного расчет искажений пример радиус = 6371 км.

У=200 км. Макс. Значение масштаба проекции на краю зоны m_y = 1 + 0,0004927 = 1\2030; искажение линии положительная поправка на проекцию в длину горизонтального положения.

Для удобства практического применения зональных координат применяют только положительно преобразованные координаты, для чего все значения у увеличивают на 500 км ; y_g = 3 415 270 м означает что точка е расположена в 3-ей зоне к западу от ее осевого меридиана и тогда действительно зональная ордината равна _д 415 270 – 500 000 = - 84 730 м

В плоской системе прямоуг координат (см.рис 1.6 а)

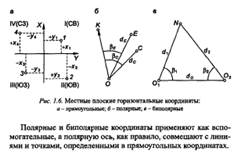
В плоской системе прямоугольных координат пренебрегают кривизной земли в левой системе координат ось абсцысс проходят параллельно осям инженерных сооружений. Координаты оси по часовой стрелке и обозначают по осевой стрелке (СВ, ЮВ , ЮЗ, СЗ). На рисунке (1.6 б) полярные координаты Е и С представлены расстоянием d_е и d_с . Биполярные координаты(см рис 1.6 в ) определяют двумя расстояниями d₁ и d₂ и двумя горизонтальными углами .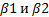

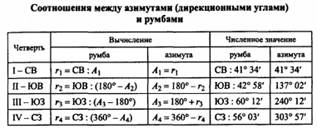
6. Ориентирование-азимуты магнитный и географический, дирекционный угол, румбы.

Ориентировать прямую линию - значит определить ее направление относительно выбранного начального направления. За начальное направлен. принимают северное направление географического меридиана либо оси абсцисс или оси магнитной стрелки. Положение географического меридиана определяют астрономическими наблюдениями или вычислениями. Направление оси абсцисс, или линии, ей параллельной в 6-градусной зоне, задано северным направлением осевого меридиана, а в местной системе координат - северным направлением линии, принятой за ось абсцисс.

Склонение магнитной стрелки. Продольная ось свободно подвешенной магнитной стрелки устанавливается по касательной к направлению силовой линии геомагнитного поля в данной точке. Вертикальная плоскость, проходящая через эту ось, определяет направление условного магнитного меридиана Мт в данной точке.

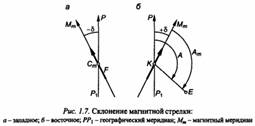
Горизонтальный угол 8 между плоскостями условного магнитного и географического меридианов в данной точке называется склонением магнитной стрелки.

Сближение меридианов

Через точки Г и Д расположенные на одной параллели, проведем касательные в плоскостях их меридианов. Касательные пересекаются в точке N под углом у, который называется углом сближения меридианов.

Для ориентирования прямых линий в геодезии применяют азимуты, дирекционные углы и румбы.

Углы ориентирования.

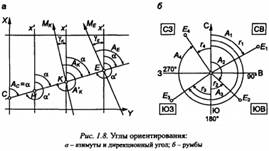
Азимутом называют горизонтальный угол, отсчитанный по ходу часовой стрелки от северного направления меридиана данной точки до направления ориентируемой линии в пределах 0-360°. От условного магнитного меридиана (северного направления магнитной стрелки) отсчитывают магнитные азимуты (азимут Ат линии КЕ - см. рис. 1.7, б), от географического меридиана - географический (геодезический) азимут (азимут А - там же), его устаревшее название - истинный азимут.

Дирекционным углом называют горизонтальный угол, отсчитанный в данной точке от северного направления линии, параллельной оси абсцисс, по ходу часовой стрелки до Направления ориентируемой линии в пределах 0-360°.

В местной системе координат дирекционный угол отсчитывается относительно северного направления частной оси абсцисс, или линий, ей параллельных. Дирекционный угол сохраняет одно и то же значение в любой точке прямолинейного отрезка. Обратный дирекционный угол а' отличается от прямого угла а на 180° и вычисляется по простой формуле а' = а ± 180°. Здесь знак «плюс» берется при а < 180° и знак «минус» при а > 180°.

Румбы.

Горизонтальный острый угол, отсчитанный от ближайшего (северного или южного) исходного направления до ориентируемого направления, называют румбом

Румб отсчитывают в пределах от 0 до 90° и дополняют обозначением его четверти по сторонам света (например, г = ЮВ : 54° 25').

В зависимости от исходного направления (магнитного, географического меридиана или оси абсцисс) различают магнитные, географические или дирекционные румбы.

7-8. Прямая и обратная геодезическая задачи

В системах плоских прямоугольных координат геодезические расчеты основаны на формулах решения прямой и обратной геодезических задач.

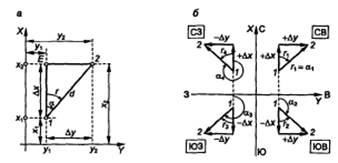
В прямой геодезической задаче известны горизонтальное проложение d прямого отрезка 1-2 (рис. 1.9, а), его дирекционный угол α, координаты 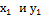начальной точки 1. Требуется вычислить координаты 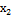и 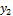точки 2.

Рис. 1.9. Прямая и обратная геодезические задачи:

а - прямая и обратная задачи; б - знаки приращений координат, дирекционные углы и

румбы при различных направлениях 1-2

Сначала вычисляют приращения координат решением прямоугольного треугольника 1-Е-2:

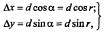
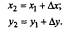
Знак приращений координат ∆х и ∆у зависит от направления отрезка 1-2 (рис. 1.9, б) и соответствует знаку cos а и sin a.

При вычислениях с использованием румба г (положительного числа) соответствующие значения ∆х и ∆у также необходимо записывать со знаком «плюс» или «минус» в соответствии с рис. 1.9, б.

Пример 1.1. Вычислить координаты х2, 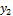точки 2, если длина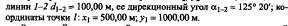

Решение. Для вычислений следует использовать дирекционный угол. Если применить румб, то его значение r1_ 2 = ЮВ: (180° - α1_2 ) = ЮВ: 54°40'. Затем найдем ∆ х = 100,00 • cos 54° 40' = 57,83 м; ∆у = 100 • sin54° 40' = 81,58 м. Определив знаки -∆х и +∆у для направления ЮВ (см. рис. 1.9, б), вычислим x2 и у2:

х2 = 500,00 - 57,83 = 442,17 м;

у2 = 1000,00 + 81,58 = 1081,58 м.

В обратной геодезическойзадаче по известным координатам х1 и у1, x2 и у2 конечных точек отрезка прямой 1-2(см. рис. 1.9, а) вычисляют горизонтальное проложение d, румб г 1_ 2 и дирекционный угол α 1_2 .

Вначале вычисляют тангенс румба (см. рис. 1,9, а):

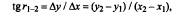
а затем численное значение румба: г = arctg (∆y/∆x).

По знакам разностей (у2 –y1) и (х2 –x1) определяют название четверти румба (см. рис. 1.9, б) и вычисляют дирекционный угол (см. табл. 1.3). Длину отрезка 1-2 находят по двум из трех следующих формул:

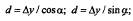d=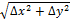

Пример 1.2. Вычислить длину d 1-2 и дирекционный угол α линии 1-2, если известны координаты точек 1 и 2: х1= 200,00 м; у1 = 400,00 м; x2 = 286,34 м; у 2 = 349,54 м.

Решение. По формуле (1.14) рассчитаем tgr1_2 = (349,54 - 400,00) / (286,34 - 200,00) = -50,46 / +86,34 = -0,58443, а также найдем arctg (∆y/∆x) = -30,299° = -30° 17,9'. По знакам +∆х (к северу) и -∆у (к западу) найдем г 1_ 2 = СЗ := 30° 17,9', затем дирекционный угол α = 360° - 30° 17,9' = 329° 42,1'. По формулам вычислим d1_2 = 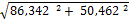= 100,00 м.

9-11. Зависимость между горизонтальными и дирекционными углами теодолитного хода. Уравнивание (увязка) горизонтальных углов

Пусть имеем две стороны хода АВ и ВС (рис.10.1) Дирекционный угол стороны АВ будем считать известным. Если обозначить через b правый по ходу горизонтальный угол, то a_ВС = a_АВ + 180° - b.

Дирекционный угол последующего направления равен дирекционному углу предыдущего направления плюс 180 и минус горизонтальный угол справа по ходу.