Статистические закономерности модификационной изменчивости
К статистическим закономерностям модификационной изменчивости относятся варианты, вариационный ряд изменчивости признака и вариационная кривая.
Модификационная изменчивость многих признаков растений, животных и человека подчиняется общим закономерностям. Эти закономерности выявляются на основании анализа проявления признака у группы особей (n). Степень выраженности изучаемого признака у членов выборочной совокупности различна. Каждое конкретное значение изучаемого признака называют вариантой и обозначают буквой ν. При изучении изменчивости признака в выборочной совокупности составляется вариационный ряд, в котором особи располагаются по возрастанию показателя изучаемого признака.
Вариационный ряд представляет ряд вариант, расположенных в порядке убывания или возрастания (например, если собрать листья с одного и того же дерева и расположить их по мере увеличения длины листовой пластинки, то получается вариационный ряд (рис. 12) изменчивости данного признака).
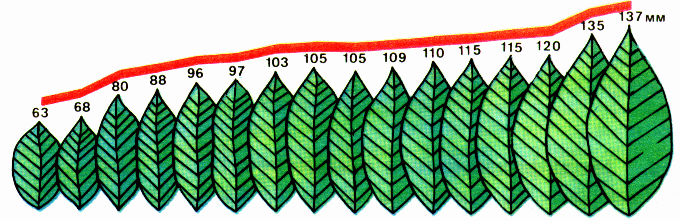
Рис. 12. Вариационный ряд листьев лавровишни (цифрами показана длина листьев).
На основании вариационного ряда строится вариационная кривая – это графическое изображение зависимости между размахом изменчивости признака и частотой встречаемости отдельных вариант данного признака (рис. 13). Частота встречаемости отдельных вариант обозначается буквой p. Например, если взять 100 колосьев пшеницы (n) и подсчитать число колосков в колосе, то это количество будет от 14 до 20 – это численное значение вариант (ν). Вариационный ряд: ν = 14-15-16-17-18-19-20. Частота встречаемости каждой варианты p = 2-7-22-32-24-8-5. Среднее значение признака встречается чаще, а вариации, значительно отличающиеся от него, – намного реже. Это называется нормальным распределением. Кривая на графике бывает, как правило, симметричной. Вариации, как большие, чем средние, так и меньшие, встречаются одинаково часто.
Наиболее типичный показатель признака – это его средняя величина, то есть среднее арифметическое вариационного ряда.
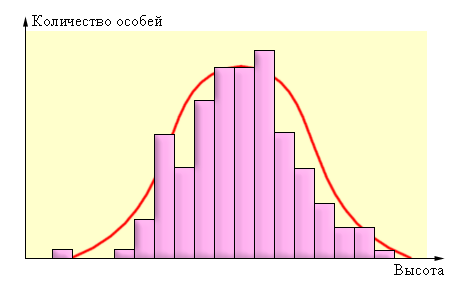
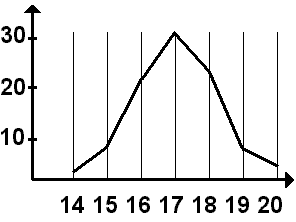
Рис. 13. Вариационная кривая.
Среднее значение данного признака легко рассчитать. Для этого используют формулу: М = Ʃ (ν х p) ∕ n, где М – средняя величина признака, в числителе сумма произведений вариант на их частоту встречаемости, в знаменателе – количество вариант (n). Для данного признака среднее значение равно 17,1.
Знание закономерностей модификационной изменчивости имеет большое практическое значение, поскольку позволяет предвидеть и заранее планировать степень выраженности многих признаков организмов в зависимости от условий внешней среды.
