Рассматривая подобие треугольников, приходим к соотношению
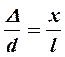 →
→ 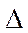 =
= 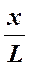 d.
d.
Условие интерференционного максимума Δ = ± k λ → 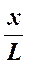 d = ± k λ
d = ± k λ
Отсюда, в опыте Юнга для светлых полос на экране х = ± k L λ/d
Расстояние Δх между соседними как светлыми, так и темными полосами на экране одинаково и равно Δх = 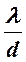 L. Чем меньше расстояние между источниками d и больше L, тем шире интерференционные полосы.
L. Чем меньше расстояние между источниками d и больше L, тем шире интерференционные полосы.
При наблюдении в белом свете все полосы, кроме центральной, которой соответствует k = 0, окрашены и число наблюдаемых полос невелико. Это связано с тем, что полосы соответствующие разным цветам при больших k перекрывают друг друга и дают равномерное освещение. В монохроматическом свете число наблюдаемых полос существенно больше.
Интерференция в тонких плёнках
|
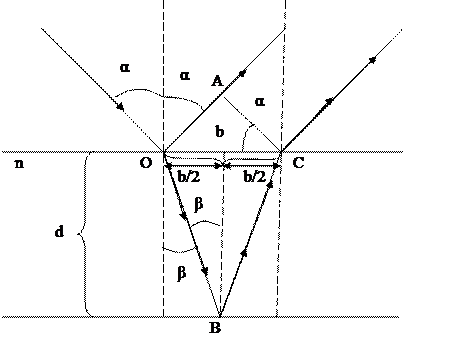
n– показатель преломления; d – толщина пленки (плоскопараллельной стеклянной пластинки);
b – расстояние между точками O и C
α – угол падения светового луча; β – угол преломления
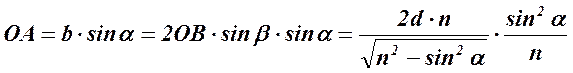
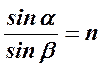
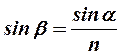
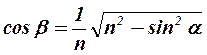
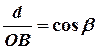
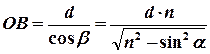
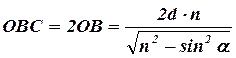
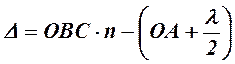
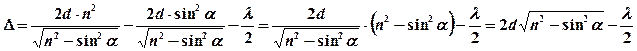
Условие max интенсивности света 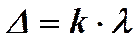 , т.е.
, т.е. 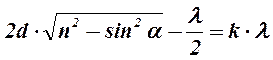
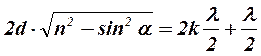
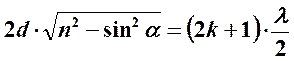 - max интенсивности света (формула через угол падения светового луча)
- max интенсивности света (формула через угол падения светового луча)
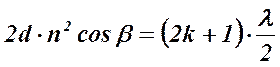 - max интенсивности света (формула через угол преломления светового луча).
- max интенсивности света (формула через угол преломления светового луча).
Полосы равной толщины
Кольца Ньютона – классический пример наблюдения полос равной толщины.
Наблюдение колец Ньютона в отраженном свете
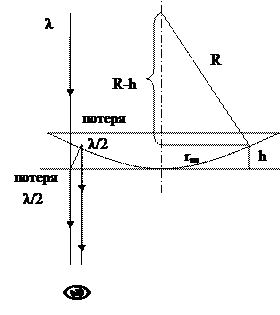
На плоской стеклянной поверхности лежит плосковыпуклая линза. Между линзой и пластиной образуется воздушная прослойка, имеющая в разрезе вид клина, т.е. места равной толщины воздушной прослойки образуют окружности радиуса r. Если R – велико, то – b соизмеримо с λ. При нормальном падении света λ лучи света, отраженные от двух сторон воздушного клина создают в отраженном свете интерференционную картину
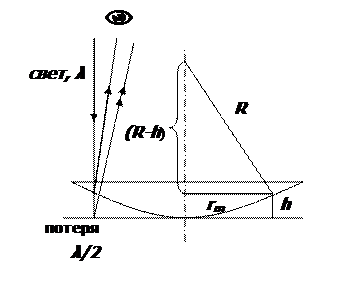

В месте контакта линзы со стеклом из-за мелких пылинок толщиной d оптическая разность хода в отраженном свете 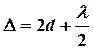 , но d <<
, но d << 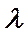 и
и 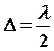 (условие min I )
(условие min I )
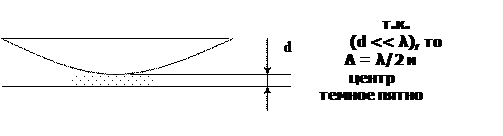
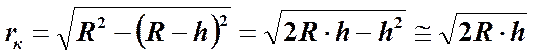
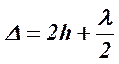
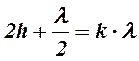 - max
- max 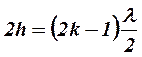 k = 1,2 …
k = 1,2 …
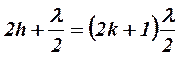 - min
- min 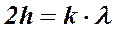 k = 1,2 …
k = 1,2 …
Радиус темных колец Ньютона в отраженном свете
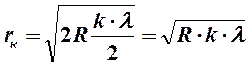 k = 0,1,2,…
k = 0,1,2,…
(k = 0 , центр - тёмное пятно)
Радиус светлых колец Ньютона в отраженном свете
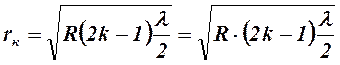 , k = 1,2 ,… или
, k = 1,2 ,… или
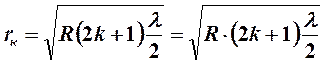 , k = 0,1,2,
, k = 0,1,2,
Наблюдение колец Ньютона в проходящем свете

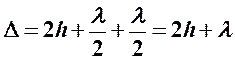
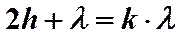 - max I
- max I 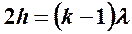
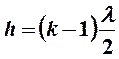
поскольку 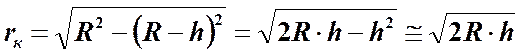 , то радиус светлых колец в проходящем свете
, то радиус светлых колец в проходящем свете
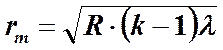 , где k = 1, 2, 3, … или
, где k = 1, 2, 3, … или
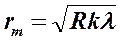 , где k= 0,1,2,…
, где k= 0,1,2,…
Просветление оптики (воздух – пленка - стекло)
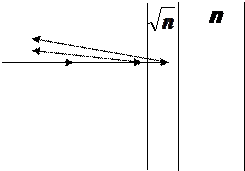
∆ = (2k+1) 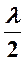 - отраженные лучи, интерфирируя, гасят друг друга (расчет ведется для
- отраженные лучи, интерфирируя, гасят друг друга (расчет ведется для 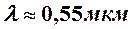 , поэтому просветленная оптика имеет голубоватую или фиолетовую окраску).
, поэтому просветленная оптика имеет голубоватую или фиолетовую окраску).
Применение интерференции
Просветление оптики. Ослабляется отражение света в оптических системах.
2. Многолучевая интерференция (в лазерной технике) – усиление определенной λ (пластинки с разными n, но разная толщина и одинаковая оптическая разность хода).
