Статистические методы, используемые в процессе анализа морфометрических показателей растений елового леса
В ходе курсовой работы применяем метод статистического распределения выборки, который заключается в перечне вариантов и соответствие им частот или относительных частот. При условии ( 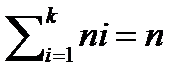 ).
).
Метод статистических распределений частот:условие( 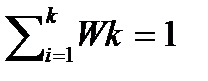 ).Нахождение относительных частот вычисляется по формуле (1)
).Нахождение относительных частот вычисляется по формуле (1)
Wi =ni/n, (1)
где ni – частота,
n –объём выборки.
Метод построения полигона относительных частот: полигоном относительных частот называется ломанная с вершинами в точках (Xi;Wi),
i=1,k.
Нахождение выборочных характеристик:
В статистике распространённой характеристикой центра группирования значений генеральной совокупности является выборочное среднее значение. Выборочным средним выборки x1, x2, xnназывают среднее арифметическое этих значений, которое обозначается  . Формула для вычисления среднего изменена в зависимости от представления выборочных данных x1, x2,…,xn.
. Формула для вычисления среднего изменена в зависимости от представления выборочных данных x1, x2,…,xn.
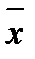 = 1/n *
= 1/n * 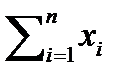 , (2)
, (2)
где 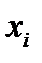 - варианты.
- варианты.
Б) Если среди выборочных значений есть повторение, т. е построено статистическое распределение частот, то применяется формула:
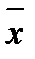 = 1/n *
= 1/n * 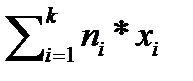 (3)
(3)
В) Для больших выборок сначала необходимо построить сгруппированное распределение частот и по нему находить значение среднего:
х = 1/n * 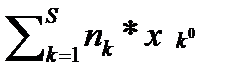 (4)
(4)
Такие характеристики как выборочная дисперсия, выборочное среднеквадратичное (ср/кв) отклонение и выборочный коэффициент вариации – дают представление о том, насколько далеко отклоняется от своего центра группирование значений выборки.
Выборочной дисперсией – s2 называется среднее арифметическое квадратов отклонений значений выборкиx1, x2,…,xn, от 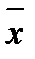 .
.
s2 = 1/n * 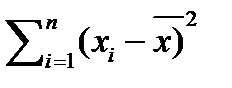 (5)
(5)
Расчётная формула для выборочной дисперсииимеет:
s2 = x2 – x, (6)
где х2= 1/n * 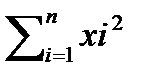 ,
,
Выборочное ср/кв отклонение Sопределяется как положительное значение квадратного корня из дисперсии:
s = 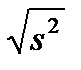 (7)
(7)
sиспользуется с s2 для характеристики изменчивости выборки и оказывается более удобным, так как имеет ту же размерность, что и значение выборки. В теории оценивания доказано, что значения sи s2 не совсем хорошо оценивают теоритическое значение дисперсии иср/кв отклонения. Dи  являются более точными значениями:
являются более точными значениями:
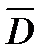 = n/n-1 * s2 (8)
= n/n-1 * s2 (8)
 =
= 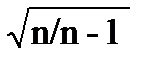 * s (9)
* s (9)
Выборочныйкоэффициет вариации используется в тех случаях, когда степень изменчивостиудобно описывать некоторой характеристикой в соответствии со средним значением.
V* = s/ 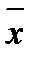 * 100 % (10)
* 100 % (10)
Метод статистической проверки гипотез:
На разных стадиях статистического исследования возникает необходимость в формулировке и проверке некоторых утверждений – гипотез.Процедура обоснованного сопоставления гипотезы с выборочными данными x1, x2,…,xnсопровождающаяся количественной оценкой степени достоверности вывода называется – статистической проверкой гипотез. Она осуществляется с помощью статистического критерия. Результат проверки гипотез может быть отрицательным (выборочные данные противоречат гипотезе), либо неотрицательными (не противоречат гипотезе). Неотрицательный результат не означает, что данные гипотезы являются наилучшими, он означает, что гипотеза является одним из возможных решений наряду с другими. Отрицательный результат – однозначный, т.е гипотеза отвергается. Нулевой называется гипотеза H0.Альтернативной конкурирующей – гипотеза H1, которая противоречит основной.
Для проверки гипотез в ходе работы применяем критерий Стьюдента Т.
Схема критерия:
