Энергия связи атомных ядер
Дефект массы. Согласно релятивистской механике масса покоя М устойчивой системы взаимосвязанных частиц меньше суммы масс покоя m1 + m2 +…+ mk тех же частиц, взятых в свободном состоянии. Разность
ΔМ = (m1 + m2 +…+ mk) – М называется дефектом массы системы частиц.
Уменьшение массы покоя свободных частиц при соединении их в устойчивую систему происходит вследствие освобождения некоторой части энергии покоя этих частиц. Выделившаяся энергия называется энергией связи.
Из закона сохранения энергии следует, что наименьшая энергия, которую нужно затратить, чтобы расчленить устойчивую систему взаимосвязанных частиц на отдельные свободные частицы, равна энергии связи.
Энергия связи прямо пропорциональна дефекту массы системы частиц ΔЕ = с2ΔМ, где с2 – коэффициент перехода от массы к энергии, численно равный квадрату скорости света в вакууме; 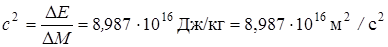 .
.
Если энергия выражена в мегаэлектрон - вольтах, а масса в атомных единицах, то с2 = 931, 44 МэВ/а.е.м.
Дефект массы ΔМ атомного ядра есть разность между суммой масс свободных протонов и нейтронов и массой образовавшегося из них ядра ΔМ = (Ζmp + Nmn) – M, где Ζ – число протонов в ядре; N – число нейтронов (N = A – Ζ); mp и mn – массы свободных протона и нейтрона; М – масса ядра.
Ядерные реакции
Символическая запись ядерной реакции может быть дана или в развернутом виде, например 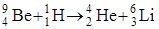 , или сокращенно 9Be(р,α)6Li.
, или сокращенно 9Be(р,α)6Li.
Обозначения частиц: p – протон, n – нейтрон, d – дейтрон, t – тритон, α – альфа-частица, γ – гамма-фотон.
При решении задач применяются законы сохранения:
числа нуклонов А1 + А2 = А3 + А4;
заряда Ζ1 + Ζ2 = Ζ3 + Ζ4;
релятивистской полной энергии
Е1 + Е2 = Е3 + Е4;
импульса 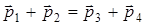 .
.
Энергетический эффект ядерной реакции Q = c2[(m1 + m2) – (m3 +m4)],
где m1 – масса покоя ядра – мишени; m2 – масса покоя бомбардирующей частицы; m3 + m4 – сумма масс покоя ядер продуктов реакции.
Если m1 + m2 > m3 +m4, то энергия освобождается, энергетический эффект положителен, реакция экзотермическая.
Если m1 + m2 < m3 +m4, то энергия поглощается, энергетический эффект отрицателен, реакция эндотермическая.
4.1. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
№ 1. Электрон в атоме водорода перешел с четвертого энергетического уровня на второй. Определить энергию испущенного при этом фотона.
Р е ш е н и е.
Для определения энергии фотона воспользуемся сериальной формулой для водородоподобных ионов:
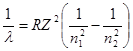 , (1)
, (1)
где l - длина волны фотона; R – постоянная Ридберга; Z – заряд ядра в относительных единицах (при Z = 1 формула переходит в сериальную формулу для водорода); n1 – номер орбиты, на которую перешел электрон; n2 – номер орбиты, с которой перешел электрон (n1 и n2 – главные квантовые числа).
Энергия фотона e выражается формулой e= hc/l . Поэтому, умножив обе части равенства (1) на hc, получим выражение для энергии фотона 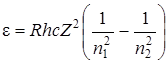 . Так как величина Rhc- есть энергия ионизации E1 атома водорода, то
. Так как величина Rhc- есть энергия ионизации E1 атома водорода, то 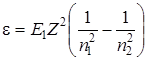 .
.
Вычисления выполним во внесистемных единицах: Е1 = 13,6 эВ; Z = 1 (заряд ядра атома водорода в относительных единицах, где за единицу заряда принято абсолютное значение заряда электрона); n1 =2; n2 = 4;
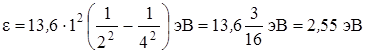 .
.
№ 2. Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность потенциалов U. Найти длину волны де Бройля для двух случаев: 1) U1 = 51 В; U2 = 510 кВ.
Р е ш е н и е.
Длина волны де Бройля для частицы зависит от ее импульса р и определяется формулой:
l = h/р, (1)
где h – постоянная Планка.
Импульс частицы можно определить, если известна ее кинетическая энергия Т. Связь импульса с кинетической энергией различна для нерелятивистского случая (когда кинетическая энергия частицы много меньше ее энергии покоя) и для релятивистского случая (когда кинетическая энергия сравнима с энергией покоя частицы).
