Вращение твёрдого тела

4.1. Две гири массами m₁=1 кг и m₂=2 кг соединены нитью, перекинутой через блок массой М = 3 кг. Найти ускорение гирь и силу натяжения нити. Трения в блоке нет.

4.2. На дисковый блок массой М=2 кг намотана нить, к концу которой привязан груз массой m=1 кг. Найти ускорения груза и силу натяжения нити.

Ответ. , .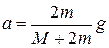

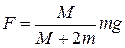4.3. С горки высотой h скатывается без проскальзывания шарик. Найти его скорость в конце горки. Обгонит ли он шайбу, соскальзывающую с той же горки без трения, если стартовали они одновременно?

Ответ. υ= .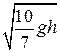

4.4. Вертикальный столб высотой h = 3 м начинает падать из вертикального положения. Найти скорость υ его конца у земли. Проскальзывания нет.

Ответ. υ= 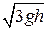=9 м/с.

4.5. Найти центр масс сплошного конуса.

Ответ. На 1/4 его высоты от основания.

4.6. Найти момент инерции сплошного конуса.

Ответ. I = 3mh³/(10R).

4.7. Найти момент инерции квадратной пластинки относительно перпендикулярной оси, проходящей через её центр.

Ответ. I=ma²/6.

Колебания

5.1. 1.395. Точка колеблется по синусоидальному закону. Амплитуда колебаний равна X, а максимальная скорость – V. Вычислить период T.

Ответ. h=H/2, s=H.

5.2. 1.396.Точка колеблется по синусоидальному закону с амплитудой X. Максимальная возвращающая сила равна F. Определить полную энергию E колебательной системы. Ответ.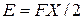

5.3. 1.397. Шарик колеблется на пружине по синусоидальному закону. При какой фазе колебаний его потенциальная энергия равна кинетической? Определить смещение x шарика в этот момент, если амплитуда равна X, а начальная фаза – нулю.

Ответ. ; .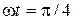

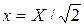5.4. 1.398.Шарик колеблется на пружине по синусоидальному закону x=Xsinwt. Найти отношение его кинетической энергии к потенциальной в момент, когда x=X/2. Сравнить интервалы времени t₁ и t₂ прохождения шариком первой (от 0 до X/2) и второй (от X/2 до X) половин амплитуды.

Ответ. ;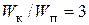

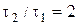
5.5. 1.399.Подвешенный груз растягивает легкую пружинку на Dl=10 см. Вычислить период колебаний груза на этой пружинке.

Ответ. 0,63 с.

5.6. 1.400.Горизонтальная подставка совершает вертикальные синусоидальные колебания с амплитудой X. При какой частоте w лежащий на подставке камень начинает отрываться от нее?

Ответ. При .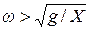

5.7. 1.410*. Сравнить ускорения математического маятника при малых ко­лебаниях в нижней и верхней точках траектории. Где оно больше и во сколько раз?

Ответ.а_верх>а_ниж; а_верх/а_ниж=l/X, где l – длина, Х – амплитуда колебаний.

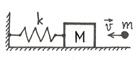5.8. 1.414. Пуля массой m попадает в брусок массой M>>m, лежащий на гладком столе и связанный со стеной пружиной жёсткостью k, и застревает в нём (см. рис.). Брусок начинает колебаться с амплитудой Х. Найти скорость пули.

Ответ.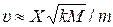

5.9. Найти период колебаний обруча, который качается на вбитом в стенку гвозде в своей плоскости. Радиус обруча R = 30 см.

5.10. Найти период колебаний стержня длиной l = 1 м, шарнирно закреплённого в его конце.

5.11. На каком расстоянии х от центра стержня длинной l находится ось качания О, период колебаний относительно которой такой же, как и относительно конца стержня?

Ответ. х=l/6; Т=2π .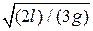

5.12. Амплитуда колебаний маятника за одну минуту уменьшилась в два раза. Во сколько раз она уменьшится за три минуты?

5.13.8.2. Шарик на пружинке оттянули и отпустили. Через какую долю периода кинетическая энергия шарика: а) сравняется с упругой энергией пружинки; б) составит треть энергии пружинки ?

Ответ. а) Δt=Т/8; б) Δt=Т/12.

5.14.8.16. Когда сыр небрежно бросили на чашку торговых пружинных весов, стрелка, качаясь с затуханием около равновесия, показала в трёх последовательных крайних отклонениях 600, 300 и 500 г. Определить массу сыра, полагая затухание весов достаточно слабым.

Ответ. m=420 г.