Вращение твёрдого тела. Центр масс
МАТЕРИАЛЫ
курса физики, ч. 1 «Механика и термодинамика»
для студентов групп ИИТ-173, УТС-120, АТП-121
(первый семестр, сентябрь-декабрь 2016 г.)
СОДЕРЖАНИЕ
Стр.
1. Экзаменационные вопросы………………………………………………….. 2
2. Вопросы теоретического минимума………………………………………… 4
3. Семинары ……………………………………………………………….….. 5
4. Литература……………………………………………………………..……. 5
5. Рейтинговые оценки в семестре …………………………………………….. 5
6. Правила представления семестровых работ………………………………... 6
7. Задачи семинаров ………………………………………………………… 10
Лектор курса
Владимир Константинович Михайлов
Волгоград 2016
1. ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ
(34 лекционных часа)
1. Движение точки в пространстве: траектория, перемещение и путь, мгновенная и средняя скорости, ускорение. Кинематические уравнения равноускоренного движения по прямой.
2. Движение точки по окружности: угловая и линейная скорости. Радиальное, касательное и угловое ускорения. Период и частота.
3. Сила. Сложение сил. Третий закон Ньютона. Инерциальные системы отсчёта. Первый закон Ньютона. Принцип относительности Галилея.
4. Второй закон Ньютона. Импульс силы. Центростремительная сила.
5. Определение силового поля. Силовые линии. Однородное и радиальное поля. Работа поля. Свойства работы: аддитивность и алгебраичность. Определение мощности. Единицы работы и мощности.
6. Определение силового поля. Определение потенциального поля. Основное свойство потенциального поля (работа по контуру). Потенциальность однородного и центрального полей.
7. Определение потенциального поля. Потенциальная энергия частицы в поле. Связь работы поля с изменением потенциальной энергии частицы. Сила как градиент потенциальной энергии.
8. Кинетическая энергия частицы и её связь с работой. Полная механическая энергия частицы и её связь с работой сторонних сил. Закон сохранения механической энергии частицы.
9. Импульс системы частиц и его изменение под действием внешних сил. Законы сохранения импульса и механической энергии системы частиц.
10. Столкновение двух частиц. Абсолютно упругий и абсолютно неупругий удары. Прямой и косой удары шаров. Преобразование скоростей при прямом абсолютно упругом ударе шаров.
11. Центр масс системы частиц. Импульс системы частиц. Уравнение движения центра масс. Центр тяжести системы частиц.
12. Момент инерции и момент импульса частицы. Вектор угловой скорости. Момент силы. Уравнение движения частицы по окружности.
Момент импульса системы частиц. Закон сохранения момента импульса системы частиц.
13. Момент инерции твёрдого тела относительно заданной оси. Аддитивность момента инерции. Вычисление момента инерции (на примерах диска и стержня). Теорема Штейнера.
14. Уравнение вращения твёрдого тела. Работа внешней силы при вращении твёрдого тела. Кинетическая энергия вращающегося тела.
15. Инерциальные системы отсчёта. Преобразование Галилея. Неинерциальные системы. Сила инерции при поступательном движении.
16. Силы инерции в равномерно вращающейся системе. Примеры.
17. Уравнение свободных незатухающих синусоидальных колебаний и его общее решение Период, частота, фаза, амплитуда. Начальные условия. Колебания шарика на пружине (пружинный маятник).
18. Уравнение свободных незатухающих синусоидальных колебаний и его общее решение Период, частота, фаза, амплитуда. Начальные условия. Малые колебания математического маятника.
19. Уравнение свободных незатухающих синусоидальных колебаний и его общее решение Период, частота, фаза, амплитуда. Начальные условия. Малые колебания физического маятника. Приведённая длина.
20. Преобразования энергии при колебаниях пружинного и математического маятников.
21. Затухающие колебания: уравнение колебаний, его решение, график решения, первичные и вторичные параметры колебательных систем с затуханием. Слабое затухание. Критическое сопротивление среды.
22. Уравнение затухающих колебаний и его решение. Потери энергии при колебаниях. Добротность колебательной системы и её связь с другими параметрами.
23. Вынужденные колебания. Переходный и установившийся процессы. Вынужденные колебания пружинного маятника. Амплитудно-частотная характеристика колебательной системы. Резонанс. Добротность.
24. Предмет термодинамики. Моль, число Авогадро, молярная масса. Оценка размеров молекул.
25. Понятие термодинамической системы. Равновесное и неравновесное состояния системы. Время релаксации. Параметры состояния и уравнение состояния. Процессы: равновесный, неравновесный, обратимый, циклический. Внутренняя энергия системы. Температура как мера средней кинетической энергии молекул. Измерение температуры.
26. Работа системы и работа над системой. Передача тепла. Первый закон термодинамики. Внутренняя энергия системы как функция её состояния. Толкование теплоты и работы в термодинамике.
27. Понятие идеального газа. Уравнение состояния идеального газа. Закон Авогадро. Эквивалентная форма уравнения состояния.
28. Удельная и молярная теплоёмкости, единицы их измерения. Теплоёмкости идеальных газов при постоянном объёме и при постоянном давлении.
29. Изопроцессы в идеальном газе. Уравнения изопроцессов. Теплоёмкости и работы при изопроцессах.
30. Адиабатный процесс в идеальном газе. Адиабатный процесс в тропосфере, снижение температуры с высотой.
31. Адиабатный процесс в идеальном газе. Изотермическая модель атмосферы. Барометрическая формула.
32. Формулировки второго закона термодинамики. Цикл Карно. Схема тепловой машины. КПД тепловой машины.
2. ВОПРОСЫ ТЕОРЕТИЧЕСКОГО МИНИМУМА
Вопросы теоретического минимума предполагают ответы на уровне понятий, определений и формулировок без доказательства. Ответы должны иллюстрироваться примерами, рисунками, формулами.
1. Что такое система отсчёта?
2. Перечислить основные и дополнительные единицы системы СИ.
3. Что такое: перемещение, путь, мгновенная и средняя скорости?
4. Записать формулы для центростремительного и углового ускорений.
5. Что такое импульс частицы? Импульс силы ?
6. Что такое центростремительная сила?
7. Сформулировать принцип относительности Галилея.
8. Что такое силовое поле?
9. Как определяется работа поля?
10. Что значит: работа поля – величина алгебраическая и аддитивная?
11. Что такое потенциальное поле?
12. Как определяется потенциальная энергия частицы в поле?
13. Связь силы и потенциальной энергии частицы в потенциальном поле.
14. Дать определения центра масс системы частиц и сплошного тела.
15. Найти центр масс сплошного конуса.
16. Когда центр масс тела не совпадает с его центром тяжести?
17. Что такое момент импульса частицы?
18. Что такое момент инерции твёрдого тела? Что такое «аддитивность»?
19. Записать уравнение вращения твёрдого тела.
20. Теорема Штейнера.
21. Записать кинетическую энергию вращающегося твёрдого тела.
22. Что такое сила инерции?
23. Что такое сила Кориолиса? Куда она направлена?
24. Уравнение синусоидальных колебаний о общий вид его решения.
25. Что такое амплитуда частота и фаза синусоидальных колебаний?
26. Что такое резонанс?
27. Дать определения: времени релаксации, логарифмического декремента затухания, добротности, слабого затухания, критического сопротивления среды.
28. Понятия процессов: равновесного, квазистатического, обратимого.
29. Что такое теплота, работа, внутренняя энергия системы? Какие из этих величин являются функциями состояния системы и что это означает?
30. Как реализовать равновесный процесс нагревания газа?
31. Сформулировать первый закон термодинамики.
32. Записать первый закон термодинамики для элементарных процессов.
33. Почему Cp >CV ?
34. Что такое число степеней свободы молекулы? Как выражаются через них молярные теплоёмкости идеального газа?
35. Как связаны молярная и удельная теплоёмкости?
36. Что такое идеальный газ? Записать уравнение состояния идеального газа в двух эквивалентных формах.
37. Что такое адиабатный процесс? Записать одно из его уравнений.
38. Почему температура тропосферы падает с высотой?
39. Записать барометрическую формулу.
40. Сформулировать второй закон термодинамики.
41. Почему в формулировке второго закона термодинамики подчёркивается, что «процесс должен быть круговым, а его результат – единственным»? Обосновать эти требования примерами.
42. Что такое тепловая машина? КПД тепловой машины.
43. Что такое цикл Карно? Каков КПД идеальной машины Карно?
44. Что такое холодильная машина? Почему её работа не противоречит второму закону термодинамики?
3. ТЕМЫ СЕМИНАРОВ (17 часов)
1. Кинематика точки.
2. Уравнения движения.
3. Работа, энергия. Законы сохранения.
4. Вращение твёрдого тела.
5. Колебания.
6. Уравнение состояния идеального газа.
7. Первый закон термодинамики. Изопроцессы.
За семестр выполняются две контрольные работы.
На выполнение каждой контрольной работы даются по две попытки в семестре – основная и резервная. При отрицательном результате контрольная работа выполняется в день экзамена по физике, а сам экзамен при этом считается не сданным по неуважительной причине.
4. ЛИТЕРАТУРА
1. И. В. Савельев. Курс общей физики. Т. 1, 2. «Наука», М., 1979.
2. И. Е. Иродов. Механика. «Физматлит», М., 2000.
3. А.А.Детлаф, Б.М.Яворский. Курс физики. «Высшая школа», М., 1989.
4. В. С. Волькенштейн. Сб. задач по общему курсу физики. М., 1973.
5. РЕЙТИНГОВЫЕ ОЦЕНКИ В СЕМЕСТРЕ
1. Лабораторные занятия – до 20 баллов.
2. Семинары и контрольные работы (две за семестр) – до 20 баллов. При этом удачное выступление у доски оценивается в 1 балл, каждая задача контрольной работы – в 2 балла.
3. Семестровые работы – до 20 баллов (первая – до 12, вторая – до 8 баллов).
Зачёты по всем лабораторным работам, двум контрольным и двум семестровым являются необходимым условием допуска к экзамену по физике.
6. правила представления семестровых работ
1. Каждый студент за семестр представляет две домашние семестровые работы: одну по разделу «Механика» и одну по разделу «Термодинамика».
2. Каждая работа сдаётся на пронумерованных листах формата А4 с односторонней записью, в опрятном виде. Работа начинается с титульного листа, в центре которого пишется (или печатается) следующее:
СЕМЕСТРОВАЯ РАБОТА № 1
по физике (раздел «Механика»)
студента группы ИИТ-173
Егорова Егора Егоровича
Работа сдана 26 октября 2016 г.
3. Условие задачи сначала записывается текстом, а затем в краткой стандартной форме: «Дано…, Определить…, Решение». Задача решается сначала аналитически, а затем подставляются численные данные.
4. Комментарии к задачам необходимы, поясняющие рисунки – желательны. Задача, не имеющая комментариев в текстовом или рисуночном виде, не рассматривается. При этом следует помнить, что всякая задача решается не «по формулам», а от законов, определений, от базовых уравнений.
5. Оценка семестровой работы зависит от срока её сдачи и от числа решённых задач. Последний срок сдачи 1-ой работы – 31 ок5тября, 2-ой работы – 15 декабря.Работы, сданные после этих сроков, оцениваются утешительным зачётным баллом (с примерным коэффициентом 0.5).
6. Нормально решённая задача, т.е. правильно и с должными комментариями, отмечается значком «+» (2 балла); решённая с ошибками, с невнятными комментариями, неряшливо, без расчётной части – значком «±» (1 балл); если решение в принципе неверно, либо же отсутствуют необходимые комментарии к формулам, − значком «−» (задача не зачтена).
Два «плюс-минуса» в каждой теме приравниваются к одному «плюсу».
7. Минимальное количество решённых задач, необходимое для зачёта данной семестровой работы, – по две любые из каждой темы, а точнее так: надо набирать минимум по два балла в каждой теме. При этом студент должен быть готов лично прокомментировать решение каждой задачи.
8. Зачтённые работы студентам не возвращаются.
ЗАДАЧИ СЕМЕСТРОВОЙ РАБОТЫ № 1 (раздел «Механика»)
1. Кинематика
1.1. Скорость лодки относительно воды υ = 1 м/с, а скорость реки u=2 м/с. Лодке надо переплыть на другой берег. Под каким углом α к траверзу реки (линии, перпендикулярной реке) должна держать курс лодка, чтобы ее снесло течением как можно меньше?
1.2. Двигатель ракеты обеспечивает ей постоянное ускорение. В течение времени t=10 мин двигатель разгонял ракету. Затем корпус ракеты повернулся на 180° и двигатель с тем же ускорением стал толкать ее к исходной точке. Сколько времени займет обратный путь ракеты до исходной точки?
1.3. Пассажиру осталось идти всего l=50 м вдоль железнодорожного пути до последнего вагона, как вдруг поезд тронулся и поехал с ускорением а=0,25 м/с2. С какой наименьшей скоростью υ должен побежать пассажир, чтобы догнать последний вагон? Сколько метров ему придется так бежать?
Уравнения движения
2.1. Кубик начинает скользить с вершины наклонной плоскости, основание которой l =2,1 м. При каком угле наклона a время соскальзывания будет минимальным, если коэффициент трения кубика k = 0,14? Каково это время?
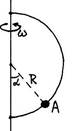2.2. Бусинка А, может свободно скользить по проволоке, изогнутой в форме полукольца радиусом R (см. рис.). Система вращается с постоянной угловой скоростью w вокруг вертикальной оси. Вычислить угол a, соответствующий устойчивому положению бусинки. В частности, найти угол α, соответствующий R=10 см, f=1 об/с.
2.3.На горизонтальном полу стоит тележка массой М, а на ней лежит брусок массой m. Коэффициент трения между бруском и тележкой равен k. При какой горизонтальной силе F, приложенной к бруску, он начнет скользить по тележке?
Законы сохранения
3.1. Человек прыгает с моста на резиновом тросе длиной l0=12 м. Жёсткость троса такова, что в спокойном состоянии под действием веса этого человека трос растягивается до длины l=20 м. Найти: 1) максимальное расстояние h от моста, на которое снизится человек; 2) максимальную кратность перегрузки, которую испытает человек в процессе полёта; 3) максимальную скорость полёта. Размерами человека и трением его о воздух пренебречь.
3.2. Шарик подвешен на нити. Его отклонили на угол α и отпустили. Вычислить ускорения шарика в верхней и нижней точках траектории и указать их направления. При каком угле α0 они будут равными по величине? Какое из них больше при α<α0?
3.3.Частица соскальзывает без начальной скорости с вершины гладкого сферического купола. Какую дугу (в градусах) частица проедет по куполу, прежде чем оторвётся от него?
Вращение твёрдого тела. Центр масс
4.1. Однородный диск массой М=600 г и радиусом R=20 см может свободно вращаться вокруг горизонтальной оси, проходящей через его центр. В верхней точке диска укрепили маленький груз массой m=100 г, и диск начал поворачиваться. Определить линейную скорость груза, когда он окажется внизу.
4.2. Горизонтальная платформа массой М = 100 кг, радиусом R = 2 м вращается с частотой n = 9,55 об/мин. На краю платформы стоит человек массой m = 50 кг. С какой частотой п0 будет вращаться платформа, когда человек переползёт к её центру? Какую работу А при этом совершит человек?
4.3. 1.322**. Найти центр масс однородной полусферической оболочки радиусом R (тонкой полусферы без крышки).
Колебания
5.1. Определить частоту ω свободных колебаний двух шариков массами m1 и m2, соединённых пружинкой жёсткостью k.
5.2. Мокрое цилиндрическое бревно длиной l=4 м плавает в воде вертикально, так что над водой находится лишь небольшая его часть. Определить период его малых вертикальных колебаний в воде, если отношение плотностей мокрого дерева и воды rд/rв=0,9.
5.3. На каком расстоянии x от середины тонкого стержня длиной l=1 м надо установить ось качания, чтобы период Т малых колебаний стержня на ней был минимальным? Определить этот период. Изобразить график Т(х).
ЗАДАЧИ СЕМЕСТРОВОЙ РАБОТЫ № 2 (раздел «Термодинамика»)