Изучение равновесия диссоциации слабых электролитов в растворах
Для изучения диссоциации слабых электролитов и определения степени и константы диссоциации часто пользуются спектрофотометрическим методом, основанном на различии в электронном спектре поглощения молекулярной и ионизированной форм данного вещества в растворе.
Пусть какая-либо кислота диссоциирует по схеме:
НА  Н+ + А–,
Н+ + А–,
Так как при данной степени диссоциации 0<α<1 в растворе находятся как молекулы НА, так и анионы А–, в спектре (в видимой и/или в ультрафиолетовой областях) раствора будут одновременно наблюдаться по крайней мере две полосы (сольватированный ион водорода не поглощает во всей УВИ области). При изменении степени диссоциации (вследствие разбавления раствора, изменения рН, температуры или природы растворителя) соотношение между интенсивностями этих полос будет меняться. В пределе при α=1 в спектре останется только одна полоса, соответствующая поглощению аниона А–. В другом предельном случае при α=0 эта полоса исчезнет, а поглощение, отвечающее молекуле НА, достигнет максимальной для данной концентрации интенсивности.
На рис. 5 представлен пример семейства кривых поглощения, отвечающих различным степеням диссоциации при различных значениях рН слабой органической кислоты параоксипропиофенона, который в воде диссоциирует следующим образом:
HO-C6H4CO-C2H5  Н+ + (О-С6Н4-СО-С2Н5) –
Н+ + (О-С6Н4-СО-С2Н5) –
Все кривые пересекаются в одной "изобестической" точке, где оптическая плотность не зависит от рН, так как интенсивность поглощения частиц обоих видов при этой длине волны одинакова.
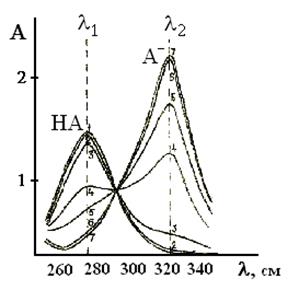
Рис.5. Спектр поглощения параоксипропиофенона при различных рН: 1–4.0; 2–5.0; 3–7.0; 4–8.0; 5–8.5; 6–11.0; 7–12.0
Слева и справа от изобестической точки оптическая плотность i-го раствора с данным значением рН будет складываться из поглощения молекулярной и анионной форм:
Ai=εHACHAl + εA-CA-l (16)
Если общая концентрация вещества в растворе равна С, а степень диссоциации кислоты в i-м растворе равна αi, то
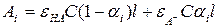 (17)
(17)
или
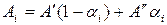 (18)
(18)
где 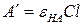 и
и 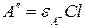 – предельные оптические плотности раствора, соответственно, в кислой (α=0) и в щелочной (α =1) среде при λ=const.
– предельные оптические плотности раствора, соответственно, в кислой (α=0) и в щелочной (α =1) среде при λ=const.
Из уравнения (18) находим:
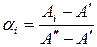 (19)
(19)
Все значения здесь должны быть измерены при одной длине волны, соответствующей максимуму поглощения молекулярной или анионной форм.
Таким образом, величину α можно найти для каждого раствора с данным значением рН, причем расчеты можно вести как по одной, так и по другой полосе поглощения. Для параоксипропиофенона λ1=273 нм, λ2=323 нм.
Термодинамическая константа диссоциации может быть выражена через активности ионов и молекул в растворе:
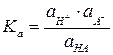 (20)
(20)
Если в первом приближении считать раствор идеальным, т.е. принять, что коэффициенты активности равны 1, то выражение для константы примет вид
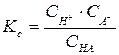 (21)
(21)
Так как 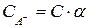 , а
, а 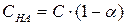 , то дробь
, то дробь 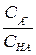 можно заменить на
можно заменить на 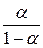 . Тогда после подстановки и логарифмирования получаем:
. Тогда после подстановки и логарифмирования получаем:
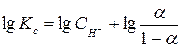 (22)
(22)
Вводя величины 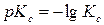 и
и 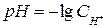 , можно записать окончательное уравнение для расчета рКс:
, можно записать окончательное уравнение для расчета рКс:
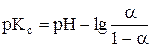 (23)
(23)
Расчет по этому уравнению дает значение логарифма идеальной, или кажущейся константы диссоциации (функции концентрации), которая зависит от ионной силы раствора. Если получить ряд значений рК при различной ионной силе раствора, можно найти значение рКа, применяя графическую экстраполяцию на нулевую ионную силу.
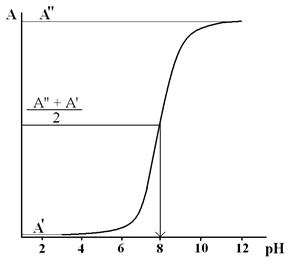
Рис.6. Графическое определение рКС параоксипропиофенона при λ2.
Значение рКС= рН1/2=8.1,
Решение по уравнению (23) можно провести и графически. Если α=0.5 то рКС = рН1/2 (второе слагаемое в равенстве (23) равно 0), где pH1/2 – так называемый "половинный показатель", т.е. значение рН, при котором 50% вещества находится в диссоциированном состоянии.
Для нахождения pH1/2 строят график зависимости А=f(рН) при λ1 и при λ2 и по полувысотам полученных кривых находят значение pH1/2=рКС. Пример графического способа расчета рКС для параоксипропиофенона при λ2 приведен на рис.6.
