Раздел 1. Основы механики

Занятие 1. Кинематика.

1. Кинематическое уравнение движения.

2. Скорость и ускорение - дифференциальные характеристики движения.

3. Средние скорость и ускорение.

4. Угловая скорость, угловое ускорение. Связь между угловыми и линейными величинами.

5. Кинематическое уравнение вращательного движения материальной точки.

6. Ускорение в плоском криволинейном движении. Нормальная и тангенциальная компоненты ускорения.

Скорость прямолинейного движения -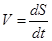

Ускорение -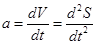

Равномерное прямолинейное движение –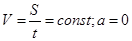

Прямолинейное равнопеременное движение –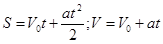

;

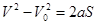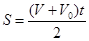
При вращательном движении угловая скорость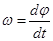

Угловое ускорение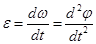

В случае равномерного вращательного движения угловая скорость 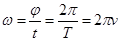, где T -период обращения, n-частота

Угловая скорость связана с линейной соотношением 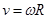, а тангенциальное и нормальное ускорение находятся следующим образом ;

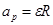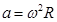
При криволинейном движении полное ускорение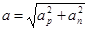

Задачи, рекомендуемые для решения:

1. Зависимость пройденного пути от времени задается уравнением 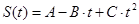, где А=6 м, В=3 м/с, С=2 м/с². Найти среднюю скорость и среднее ускорение тела в интервале времени от 1 с до 4 с. Построить график пути, скорости и ускорение для промежутка времени от 0 до 5 с через 1 с.

2. Зависимость пройденного телом пути от времени задается уравнением 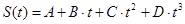, где С=0,14 м/с², D=0,01 м/с³. Через сколько времени после начала движения ускорение тела будет равно 1 м/с²? Чему равно среднее ускорение тела за весь этот промежуток времени?

3. Колесо радиусом 10 см вращается с постоянным угловым ускорением e=p рад/с². Найти для точек на ободе колеса к концу первой секунды после начала движения угловую скорость, линейную скорость, тангенциальное ускорение, нормальное ускорение, полное ускорение и угол, составляемый направлением полного ускорения с радиусом колеса.

4. Точка движется по окружности так, что зависимость пути от времени задается уравнением 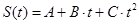, где В=-2 м/с и С=1 м/с². Найти линейную скорость точки, ее тангенциальное, нормальное и полное ускорение через 3 с после начала движения, если известно, что нормальное ускорение точки при t=2 с равно a_n=0,5 м/с².

5. Тело движется из состояния покоя равноускоренно. Во сколько раз путь. Пройденный телом за восьмую секунду , будет больше пути, пройденного телом за третью секунду?.

6. Два тела бросают с высоты 20 м со скоростью 15 м/с каждое. С какими скоростями упадут тела на землю, если первое брошено вертикально вверх. А второе – горизонтально?

7. Противотанковое орудие стреляет прямой наводкой по танку. Разрыв снаряда на батарее был замечен через 0,6 с, а звук от разрыва услышан через 2,1 с после выстрела. Скорость звука 340 м/с. На каком расстоянии находится танк? С какой горизонтальной скоростью летел снаряд?

8. С крыши здания высотой 16 м через одинаковые промежутки времени падают капли воды, причем первая ударяется о Землю, когда пятая отделяется от крыши. Найти расстояние между отдельными каплями в момент удара первой капли о Землю.

9. Пловец переплывает реку по прямой, перпендикулярной берегу. Определить скорость течения, если скорость пловца относите льно воды в 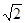раз больше скорости течения. Скорость пловца относительно берега равна 0,5 м/с.

10. Тело прошло половину пути со с скоростью 6 м/с, а другую половину со скоростью 4 м/с. Какова средняя скорость движения автомобиля?

Занятие 2. Динамика материальной точки.

1. Уравнение движения материальной точки в дифференциальной форме.

2. Силы в механике.

3. Динамика материальной точки, движущейся по окружности.

4. Импульс тела. Закон сохранения импульса.

Основной закон динамики (второй закон Ньютона) -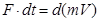

Если масса постоянна, то 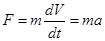, где а – ускорение, приобретаемое телом массы под действием силы F.

Сила, вызывающая упругую деформацию тела Х, пропорциональна величине деформации 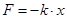направлена в сторону, противоположную деформации. (k – коэффициент упругости)

Две материальные точки (т.е. тела, размерами которых пренебрегают по сравнению с расстояниями, проходимыми этими телами) притягиваются друг к другу с силой 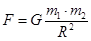, где G-постоянная тяготения (G= 6,67×10^-11 Н/м²×кг²).

Сила, возникающая при движении одного тела по поверхности другого сила трения 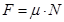, где m - коэффициент трения, N – сила реакции опоры (сила нормального давления).

Импульс тела 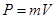. Закон сохранения импульса: Импульс замкнутой системы тел, между которыми действуют консервативные силы, остается постоянным.

Задачи, рекомендуемые для решения:

1. Деревянный брусок находится на наклонной плоскости. С какой наименьшей силой надо прижать брусок к плоскости, чтобы он остался в покое? Масса бруска 0,2 кг, длина наклонной плоскости 1 м, высота 0,5 м, коэффициент трения бруска о плоскость равен 0,4.

2. Шар массой 4 кг, подвешенной на нерастяжимой и невесомой нити длиной 1 м совершает колебания в вертикальной плоскости. Найти силу натяжения нити, когда она образует с вертикалью угол 60⁰, а скорость шара равна 1,5 м/с.

3. Горизонтально расположенный диск вращается вокруг вертикальной оси, делая 0,15 оборотов в секунду. Наибольшее расстояние от оси вращения, на котором тело удерживается на диске, равно 10 см. ему равен коэффициент трения тела о диск?

4. Автомобили на автодроме испытываются на скорости 120 км/ч. Под каким углом к горизонту должно быть наклонено полотно дороги на повороте с радиусом закругления 110 м, чтобы движение автомобиля было наиболее безопасным даже в гололедицу?

5. Доска массой 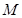может двигаться без трения по наклонной плоскости, образующей угол 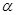с горизонтом. С каким ускорением должна бежать по доске собака массой 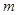, чтобы доска не соскальзывала с наклонной плоскости? Каким должен быть коэффициент трения между лапами собаки и доской, чтобы задача имела решение?

6. На бруске, находящемся на горизонтальной плоскости, установлен подвес с нитью длиной l и грузом массой 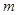. Нить с грузом отклонили на угол 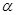и отпустили. Определите массу бруска, если он сдвинулся, когда угол между нитью и вертикалью был равен 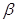. Коэффициент трения бруска о плоскость .

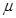7. Гладкий клин массы 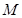может скользить по горизонтальной плоскости. На его грань, образующую угол a с горизонтом, положен гладкий брусок массы 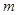. Найти ускорение клина. Трением пренебречь.

8. Шарик массой 10 г падает с высоты 2 м и упруго отражается от установленного на неподвижной тележке щита, плоскость которого наклонена к горизонту под углом 45⁰. Найти скорость тележки после отражения шарика. Трением пренебречь. Масса тележки со щитом 90 г.

9. Из двух соударяющихся абсолютно упругих шаров шар большей массы до удара покоился. В результате прямого удара меньший шар потерял 3/4 своей кинетической энергии. Чему равно отношение масс шаров?

10. Три одинаковых упругих шарика висят на параллельных нитях одинаковой длины, касаясь друг друга. Один из шариков отклоняют перпендикулярно к прямой, соединяющей центры двух других шариков, и отпускают. Найдите скорость шариков после соударения, если в момент удара налетающий шарик имел скорость .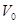

Занятие 3. Работа. Законы сохранения.

1. Работа постоянной и переменной сил.

2. Связь работы с изменением кинетической энергии.

3. Потенциальная энергия, ее виды.

4. Связь силы с потенциальной энергией.

5. Закон сохранения энергии в механике.

6. Задачи на совместное применение законов сохранения.

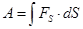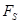Работа силы F при перемещении S может быть выражена следующей формулой , где –проекция силы на направление пути, 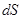– величина участка пути.

В случае постоянной силы, действующей под неизменным углом к перемещению, имеем 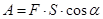, где 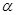- угол между силой 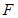и перемещением .

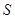Мощность определяется по формуле .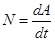

В случае постоянной мощности 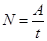, где 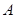– работа, совершаемая за время .

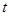Мощность может быть найдена по формуле 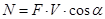, т.е мощность определяется произведением скорости движения на прорекцию силы на направление движения.

Кинетическая энергия тела массой m, движущегося со скоростью v, равна .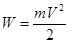

Формула потенциальной энергии имеет разный вид в зависимости от характера действующих сил.

Потенциальная энергия тела, поднятого над поверхностью Земли равна 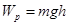, потенциальная энергия упруго деформированного тела .

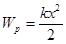Задачи, рекомендуемые для решения:

1. Вертикально расположенная пружина соединяет два груза. Масса верхнего груза 2 кг, а нижнего 3 кг. Когда система подвешена за верхний груз, длина пружины равна 10 см. Если же систему поставить на подставку, длина пружины оказывается равной 4 см. Определите длину ненапряженной пружины.

2. Бетонная однородная свая массой m лежит на две водоема глубиной 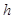, большей, чем длина сваи 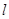. Привязав трос к одному концу сваи, ее медленно вытаскивают из воды так, что центр тяжести сваи поднимается на высоту 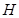от поверхности воды ( 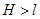). Какая работа совершается при этом? Плотность бетона в 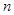раз больше плотности воды. Силами сопротивления можно пренебречь.

3. Частица с кинетической энергией 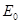упруго сталкивается с такой же неподвижной частицей и откло няется от первоначального направления на угол, равный 60°. Определите кинетические энергии частиц после со ударения

4. На концах и в середине невесомого стержня длиной l расположены одинаковые шарики. Стержень ставят вертикально и отпускают. Считая, что трение между плоскостью и нижним шариком отсутствует, найдите скорость верхнего шарика в момент удара о горизонтальную поверхность.

5. Конькобежец массой 60 кг бросает в горизонталь ном направлении камень массой 2 кг со скоростью 15 м/с. На какое расстояние откатится при этом конькобежец, если известно, что коэффициент трения полозьев о лед равен 0,02?

6. Брусок массой 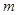равномерно втягивают за при вязанную к нему веревку на высоту 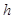по доске, угол наклона которой к горизонту равен 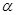. Веревка параллельна доске. Коэффициент трения бруска о доску равен 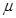. Найдите энергию, которая идет на нагревание доски и бруска.

7. Вертикально расположенная пружина соединяет два груза. Масса верхнего груза 2 кг, а нижнего 3 кг. Когда система подвешена за верхний груз, длина пружины равна 10 см. Если же систему поставить на подставку, длина пружины оказывается равной 4 см. Определите длину ненапряженной пружины

8. Камень массой 200 г упал с некоторой высоты. Падение продолжалось 1,43 с. Найти кинетическую и потенциальную энергию камня в средней точке траектории. Сопротивление воздуха пренебречь.

9. С наклонной плоскости высотой 1 м и длиной 10 м скользит тело массой 1 кг. Найти кинетическую энергию тела у основания плоскости, расстояние пройденное телом на горизонтальном отрезке пути до остановки, если коэффициент трения равен 0,5.

10. Работа, затраченная на толкание ядра, брошенного под углом 30 градусов к горизонту, равна 216 Дж. Через сколько времени и на каком расстоянии от места бросания упадет ядро, если его масс 2 кг. Сопротивление воздуха пренебречь.

Занятие 4. Динамика вращательного движения.

1. Момент силы, момент импульса, момент инерции материальной точки и твердого тела.

2. Уравнение динамики вращательного движения.

3. Момент импульса относительно точки и оси.

4. Закон сохранения момента импульса.

5. Работа постоянного момента силы.

6. Кинетическая энергия вращательного движения.

Момент 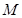силы 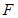относительно какой-либо оси вращения определяется формулой 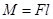, где l – расстояние от оси вращения до прямой, вдоль которой действует сила.

Моментом инерции материальной точки относительно оси вращения называется величина 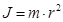, где m - масса материальной точки, r - расстояние точки до оси.

Момент инерции твердого тела относительно его оcи вращения 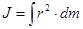, где интегрирование должно быть распространено на весь объем тела. В отдельных случаях можно получить следующие формулы моментов инерций различных тел:

1) момент инерции сплошного однородного цилиндра относительно оси вращения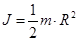

2) момент инерции полого цилиндра с внутренним радиусом 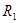и внешним радиусом 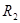относительно оси цилиндра .

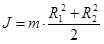3) момент инерции однородного шара радиуса R относительно оси, проходящий через его центр .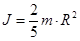

4) момент инерции однородного стержня относительно оси, проходящей через его середину перпендикулярно его длине , .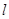

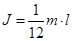Если для любого тела известен его момент инерции 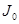относительно оси, проходящей через центр тяжести, то момент инерции относительно любой оси, параллельной первой, может быть найден по формуле Штейнера 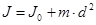, где m - масса тела, l - расстояние от центра тяжести тела до оси вращения.

Основной закон динамики вращательного движения выражается уравнением 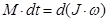, где 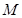- момент сил, приложенных к телу, момент инерции которого равен 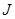; 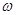- угловая скорость вращения тела.

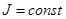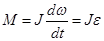Если , то , где 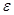- угловое ускорение, приобретаемое телом под действием вращающегося момента .

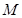Кинетическая энергия вращающегося тела 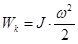, где 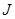- момент инерции тела и 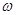- его угловая скорость.

Задачи, рекомендуемые для занятий:

1. К ободу однородного диска радиусом 0,2 м приложена постоянная касательная сила 98 Н. При вращении на диск действует момент сил трения 0,5 Нм. Найти вес диска, если известно, что диск вращается с постоянным угловым ускорением 100 рад/с².

2. Однородный диск радиусом 0,2 м и весом 50 Н вращается вокруг оси, проходящей через его центр. Зависимость угловой скорости вращения диска от времени задается уравнением 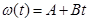, где В=8 рад/с². Найти величину касательной силы, приложенной к ободу диска. Трением пренебречь.

3. К ободу колеса, имеющего форму диска, радиусом 0,5 м и массой 50 кг приложена касательная сила 10 Н. Найти угловое ускорение колеса. Через сколько времени после начала действия силы колесо будет иметь 100 об/с?

4. На барабан радиусом 0,5 м намотан шнур, к концу которого привязан груз 10 Н. Найти момент инерции барабана, если известно, что груз опускается с ускорением 2 м/с².

5. Диск весом 2 Н катится без скольжения по горизонтальной плоскости со скоростью 4 м/с. Найти кинетическую энергию диска.

6. Диск весом 1 Н и диаметром 60 см вращается вокруг оси, проходящей через центр перпендикулярно его плоскости, делая 20 об/с. Какую работу надо совершить, чтобы остановить диск?

7. Шар диаметром 6 см катится без скольжения по горизонтальной плоскости, делая 4 об/с. Масса шара 0,25 кг. Найти кинетическую энергию катящего шара.

8. На барабан радиусом 20 м, момент инерции которого 0,1 кг×м², намотан шнур, к концу которого привязан груз 0,5 Н. До начала вращения высота груза над полом равна 1 м. Найти через сколько времени груз опустится до пола. Найти кинетическую энергию груза в момент удара о пол и натяжение нити. Трением пренебречь.

9. На барабан радиусом 0,5 м намотан шнур, к концу которого привязан груз 10 Н. Найти момент инерции барабана, если известно, что груз опускается с ускорением 2 м/с².

10. Карандаш, поставленный вертикально падает на стол. Какую угловую и линейную скорость будет иметь в конце падения середина карандаша? Конец карандаша? Длина карандаша 15 см.