Технология решения физических задач

Под технологией решения задачи понимают совокупность приемов и операций, выполнение которыхприводит к ответу на вопрос задачи, к нахождению связи между искомым и заданным в ее условии.

В психологии процесс мышления чаще всего определяется как аналитическо-синтетический. Логические приемы, осуществляемые при решении задач, также в себя включают анализ и синтез, которые сопровождают друг друга. В то же время аналитический и синтетический приемы часто рассматривают раздельно хотя это деление является условным.

При использовании аналитического приема решение задачи начинают с анализа вопроса задачи и записи формулы, в которую входит искомая величина. Затем для величин, содержащихся в этой формуле, записывают уравнение, устанавливающее их связь с величинами, заданными в условии.

При использовании синтетического приема решение задачи начинают с выяснения связей величин, данных в условии задачи, с другими до тех пор, пока в уравнение в качестве неизвестной не войдет искомая величина.

Деятельность учителя при решении задач заключается в обучении учащихся решению физических задач, что представляет собой систему приемов (или технологию), реализация которых приводит формированию у учащихся умений решать задачи.

Решение любой задачи включает в себя несколько этапов. При обучении учащихся необходимо прежде всего сформировать у них представления об этих этапах и необходимости следовать им при решении задачи.

Первый этап решения задачи - чтение и уяснение условия.

Условие задачи читает либо сам ученик, либо учитель. Текст задачи читается без спешки, при необходимости повторяется, учащимся разъясняются незнакомые термины и понятия. Полезно проанализировать условие, определив, какое явление описано в задаче что дано, что надо найти. На первых этапах обучения решению задач полезно просить учащихся пересказать условие задачи.

Второй этап решения задачи - краткая запись условия задачи. Условие записывают столбиком, при необходимости оставляют место для записи табличных данных, потребность в которых ус­танавливается при анализе задачной ситуации.

Третий этап решения задачи - перевод заданных значений физических величин в Международную систему единиц (СИ). К неукоснительному выполнению этого этапа следует приучать учащихся с начальных классов, что обусловлено в том числе и затруднения­ми, испытываемыми учащимися при выполнении этой работы. В дальнейшем допустимо использование внесистемных единиц, разрешенных к употреблению.

Четвертый этап решения задачи - анализ описанной в ней заданной ситуации. Итогом выполнения этого этапа является модель задачной ситуации.

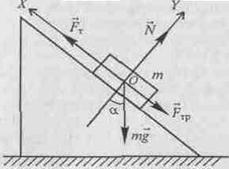
В ходе анализа устанавливают, какой физический объект описывается в задаче, какие происходят изменения состояния объекта, что является их причиной. Анализ задачной ситуации сопровождают рисунком, схемой, чертежом. В задачах по механике выбирают систему отсчета, анализируют взаимодействия, изображают силы.

Важным при анализе задачной ситуации является обсуждение всех допущений, которые делают при ее решении (факторов, которыми можно пренебречь), например пренебрежение размерами тела (материальная точка), массой нити, связывающей движущиеся тела (одинаковость ускорений тел), теплообменом с окружающей средой (изолированная система) и т.п.

Пятый этап решения задачи - создание математической модели решения задачи (составление плана решения, запись уравнении, решение задачи в общем виде, т.е. получение выражения, связы­вающего искомую величину с данными).

Шестой этап решения задачи - вычисления. Перед выполнением вычислений целесообразно осуществить проверку полученного выражения по единицам величин. Такая проверка позволяет подставить в расчетную формулу лишь численные значения величин без соответствующих единиц. Если проверка не осуществляется, то учащиеся должны подставлять в формулу значения величин (численные значения с соответствующими единицами).

Седьмой этап решения задачи - проверка ответа и его анализ. При анализе ответа устанавливают его реальность и его измене­ние при учете тех факторов, которыми пренебрегали при составлении физической модели задачной ситуации.

Этапы решения задачи представляют собой определенную последовательность действий и в этом смысле могут рассматриваться как алгоритм. Этот алгоритм является общим и содержит последовательность действий, не зависящую от того, к какому разделу курса физики относится задача. Возможно - составление частных алгоритмов решения задач или последовательности действии при решении задач по тому или иному разделу курса физики по той или иной теме.

Алгоритм, который используется в обучении, отличается от математического алгоритма меньшей жесткостью. Поэтому его называют алгоритмическим предписанием или предписанием алго­ритмического типа.

Загрузка...

Алгоритмическое предписание - точное, общепринятое выполнение в определенной последовательности элементарных операций для ре­шения любой из задач, принадлежащих к некоторому классу или типу.

В качестве примера приведем алгоритм решения задач на газо­вые законы.

1. Чтение и разъяснение условия задачи.

2. Краткая запись условия задачи.

3. Перевод значений величин в СИ.

4. Анализ задачной ситуации:

- выделить объект (газ), состояние которого исследуется;

- сделать рисунок, отметив параметры, характеризующие каждое состояние газа;

- установить, какие параметры газа изменяются;

- переформулировать условие задачи на языке физической модели.

5. Создание математической модели задачи:

-записать уравнение Клапейрона, если неменяются масса и состав газа;

-записать формулу одного из газовых законов, если не меняются масса и состав газа и один из параметров его состояния;

-записать уравнение Менделеева-Клапейрона, если меняются масса и состав газа, а также параметры его состояния;

- записать дополнительные уравнения;

- выразить искомую величину.

6. Выполнение вычисления.

7. Проверка и анализ ответа.

Работа по формированию у учащихся алгоритмического приема решения задач может быть построена по-разному в зависимости от уровня подготовки учащихся.

В классе с сильным составом учащиеся сами составляют и записывают алгоритмическое предписание, решив задачи самостоятельно или с помощью учителя. В классе, учащиеся которого не обладают высокими физико-математическими способностями, учитель дает алгоритмическое предписание в готовом виде и показывает его применение к решению задачи. В классе со слабым составом учащихся предписание дается в готовом виде и отрабатывается каждое его действие.

Полезно на первых этапах обучения учащихся решению задач определенного класса повесить плакат с последовательностью действий или выписать их на доске.

Применение алгоритмических предписаний имеет определенные границы. В частности, такие детализированные предписания при обучении учащихся решению творческих задач невозможны и нецелесообразны, хотя общие этапы деятельности могут быть определены и в этом случае.

При анализе задачной ситуации может быть использован метод графов. Он позволяет лучше уяснить аналитико-синтетический прием решения задачи, наглядно представить процесс анализа задачи, последовательность действий при ее решении.

Граф - это совокупность множества точек (вершин) и множества прямых (ребер), соединяющих эти точки. Ориентированный граф - такой, ребра которого имеют определенное направление.

Рассмотрим применение метода графов на примере следующей задачи.

Задача. Сила тока в спирали нагревателя 0,6 А. Сопротивление спирали 60 Ом. Определите изменение температуры воды массой 6 кг, если нагреватель работал 7 мин.

При анализе задачи выясняют, что вода нагревается за счет энергии, выделяющейся при прохождении по спирали электри­ческого тока. При этом считают, что все выделяющееся количе­ство теплоты пошло на нагревание воды, и пренебрегают поте­рями на нагревание сосуда, в который налита вода, окружающего воздуха и др.

Рассуждения ведутся в следующей логической последователь­ности: чтобы найти разность температур Дг, нужно знать количе­ство теплоты (0п), полученное водой, ее массу (т) и удельную те­плоемкость (с). Чтобы найти количество теплоты (бот), отданное спиралью при прохождении по ней электрического тока, нужно знать сопротивление спирали, силу тока и время ее работы т.

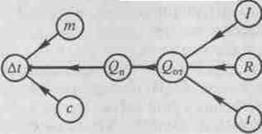Рис. 1

По ходу рассуждений выстраивают граф (рис.1), вершинам которого являются физические величины, а ребрами - связи между ними. После построения графа ребрам приписывают направления соответствующего поиска решения задачи.

Затем записывают уравнения, число которых равно числу вершин графа, в которые входят или из которых выходят не менее двух ребер. В данной задаче таких вершин три, следовательно, уравнений - три:

Q_от = I²Rτ; Q_от = Q_п; Q_п = const

Окончательно: Δt = I²Rτ / cm

Физические задачи решают на всех основных видах занятий - на уроках физики, на внеклассных занятиях, на внешкольных мероприятиях.

Задачи занимают разное место на уроке в зависимости от той дидактической цели, которую преследует их решение. Тренировочные вычислительные и простые качественные задачи решают после объяснения нового материала для его иллюстрации и закрепления.

Задачи решают в начале урока при повторении учебного материала или проведении проверки усвоения материала, в конце урока при закреплении изученного материала. Перед объяснением нового материала задачи решают и для актуализации знаний учащихся, и для создания проблемной ситуации.

Для обучения учащихся решению задач проводят, как правило, специальные уроки, которые находят отражение в календарном плане учителя.

Процесс обучения учащихся решению задач планируется так же, как и любая деятельность учителя. При этом формирование умения решать задачи следует начинать с простых задач, постепенно шаг за шагом усложняя их. В противном случае учащимся приходится прикладывать большие усилия для преодоления возникающих трудностей. Подбирая задачи по возрастанию степени сложности, учитель выстраивает определенную систему. Примером такой системы может служить система задач по динамике, приведенная ниже:

- задачи на движение одного тела при действии силы тяжести;

- задачи на движение одного тела при действии силы упругости;

- задачи на движение одного тела при действии силы трения;

-задачи на движение одного тела в вертикальном направле­нии, в горизонтальном направлении, на наклонной плоскости при действии двух сил;

- задачи на движение одного тела при действии трех сил;

- задачи на движение связанных тел: в вертикальном направлении; в горизонтальном направлении; одного - в горизонталь­ном направлении, другого - в вертикальном; одного - в вертикальном направлении, другого - на наклонной плоскости.

Физические задачи широко применяются при проверке знаний и умений учащихся. Чаще всего это осуществляется в виде контрольных работ.

Много задач учащиеся решают самостоятельно в виде домашних заданий. Учитель практически каждое теоретическое домашнее задание комбинирует с физическими задачами по изучаемому материалу. В ряде случаев целесообразно давать учащимся рекомендации по решению задач, которые предложены в качестве домашнего задания. Сложные задачи, оказавшиеся трудными для учащихся при решении их дома, надо решить в классе на следующем уроке. Можно предложить показать решение задачи ученика, сумевшего решить ее, либо решить самому учителю на доске с со­ответствующими пояснениями.

Задачи решают и на внеклассных занятиях. Это может быть кружок по решению задач для учащихся, интересующихся физи­кой, занятия с учащимися по подготовке к экзамену по физике (если он запланирован) или при подготовке желающих учеников к конкурсным (вступительным) экзаменам в вузы. В этих случаях решают в основном сложные задачи. Задачи решаются и на факультативных занятиях по физике.

ДОПОЛНИТЕЛЬНЫЙ МАТЕРИАЛ

Деятельность учителя физики по формированию научного мировоззрения учащихся

Фундаментом мировоззрения является система обобщенных знаний. Это означает, что:

- при формировании знаний учащихся о важнейших физических понятиях и идеях выделяются их мировоззренческие аспекты (например, при введении понятия импульса можно остановиться на том, что это понятие отражает связь материи и движения, так как импульс определяется как произведение массы - характеристики материального объекта и скорости - характеристики движения);

-дается диалектико-материалистическое истолкование явлений и законов природы и учащиеся подводятся к самостоятель­ным обобщениям философского характера (например, изучая с учащимися закон Ома для полной цепи, можно обратить их внимание на то, что этот закон связан с законом сохранения и превращения энергии и, следовательно, с идеей неуничтожимости и несотворимости движения и материи);

- формируются знания учащихся о методах физического исследования, об общей картине мира и отдельных этапах познания природы физической наукой (например, на основе организации всех видов учебного физического эксперимента обсуждаются осо­бенности экспериментального метода познания в науке);

- проводится специальная работа по обеспечению усвоения знаний мировоззренческого характера и по проверке усвоения этих знаний.

Для формирования личных взглядов и убеждений учащихся учитель должен отказаться от догматического стиля в преподавании и основные усилия направить на организацию познавательной деятельности учащихся, причем важно, чтобы учащиеся не только самостоятельно работали для получения того или иного знания, но и усваивали саму деятельность, в ходе которой это знание может быть добыто. Ведь в основе убеждения лежит уверенность в истинности знания. Эта уверенность не может появиться, если знания «даются» в готовом виде или не ясен путь их получения самим учеником. Кроме того, учителю необходимо в своей работе максимально использовать различные способы воздействия на эмо­циональную сферу учащихся, ибо без эмоций не происходит форми­рования взглядов и убеждений.

Например, на уроке в одной из московских школ при изучении явления электромагнитной индукции учитель намеренно допускал ошибки, аналогичные тем, которые имели место в истории науки, и вносил магнит в катушку при разомкнутом ключе и лишь потом замыкал цепь с гальванометром. Учитель изображал стремление найти неисправность в установке и «играл» огорчение от неудач. Как актер в театре, учитель подвел учащихся к эмоциональной кульминации урока, изобразил крайнее огорчение и, отвернувшись, в сердцах выхватил магнит из катушки, которая на сей раз будто бы случайно была соединена с гальванометром.

Отклонение стрелки прибора вызвало у учащихся бурную эмоциональную реакцию, ведь они тоже расстроились, потому что опыт не получался, и даже допускали скептические высказывания типа: «Никакого индукционного тока нет!» И пусть на этом уроке было шумно, главное - учащиеся переживали ситуацию, принимали происходящее на уроке близко к сердцу. Тем самым урок несомненно способствовал формированию убежденности учащихся в том, что опыт является источником знаний.

Большую роль призвано сыграть рассмотрение ошибок и заблуждений, имевших место в ходе развития физической науки, поскольку, прежде чем учить отстаивать свою позицию, целесообразно показать уже происходившую в истории науки борьбу по той или иной проблеме.

Основным же в работе учителя по формированию взглядов и убеждений учащихся должно быть специальное создание на уроках ситуаций, в которых учащиеся вынуждены будут, преодолевая некоторые препятствия, отстаивать свою точку зрения.

Ситуации, в которых учащиеся должны отстаивать свою точку зрения, могут быть смоделированы в форме диспута с вымышленным собеседником. Например, учащимся может быть предложено задание: «Ответьте вашему собеседнику, если он утверждает, что частицы жидкости и газа движутся, а частицы твердого тела - нет».

Вооружить учащихся умением преодолевать препятствия могут и задания со скрытой «провокационностью». Например, предлагая учащимся ответить на вопрос: «Куда направлена и к чему приложена сила, действующая со стороны проводника с током на магнитное поле?» - учитель создает ситуацию, когда ученик вынужден обнаружить знание того, что третий закон Ньютона выполняется лишь в рамках концепции дальнодействия и, следовательно, не может быть применен к взаимодействию вещественного и полевого объектов. Но кроме того, попав в эту ситуацию, ученик должен обнаружить и убежденность в том, что истина конкретна (в данном случае у третьего закона Ньютона есть сфера действия, и нет ничего удивительного в том, что существуют случаи, когда этот закон не может быть применен).

С целью развития диалектического мышления учитель должен, прежде всего, создавать на уроках ситуации с диалектическим противоречием. Диалектическое противоречие предполагает «подчинение» ситуации формуле «и то, и другое» - «ни то, ни другое од­новременно» в отличие от формулы «или - или».

Загрузка...

Поясним сказанное на примерах. При решении физических задач часто приходится сравнивать разные значения физических величин. Отвечая на вопрос, какое из значений больше, учащиеся разрешают формально-логическое противоречие (либо А > В, ли­бо В > А - других вариантов нет). Есть более сложный вид противоречий (можно условно назвать его промежуточным между формально-логическим и диалектическим), когда на вопрос типа «или-или» следует ответ «и то, и другое».

Например, обсуждая с учащимися явление трения, учитель традиционно задает вопрос: «Хорошо, что существует трение, или плохо?» - и в ответ учащиеся рассказывают о том, когда с трением приходится бороться, а когда без трения не обойтись. К такому же виду противоречий можно отнести и те, что «подчиняются» формуле «ни то, ни другое». Скажем, на вопрос о вреде или пользе инертности можно дать ответ: «Инертность и не вредна, и не полезна (ни то, ни другое), инертность - это свойство тел, а вот учитывать его можно по-разному». Собственно диалектическое противоречие можно выявить, например, путем постановки вопроса: «К каким колебаниям, свободным или вынужденным, следует отнести автоколебания?» В результате обсуждения этого вопроса с учащимися должен быть получен вывод о том, что автоколебания одновременно обладают свойствами и свободных, и вынужденных колебаний, не являясь ни теми, ни другими. Автоколебания - диалектическое единство противоположностей - свободы и необходимости.

При проведении работы по формированию мировоззрения учащихся на уроках физики следует иметь в виду, что можно создавать у них представления о природе и ее познании, не формулируя никаких философских обобщений, не употребляя философских терминов. Это должно происходить за счет характера, содержания, стиля трактовки основных вопросов курса физики. Однако нельзя полностью отказываться от использования философской терминологии на уроках физики. Постоянно имея в виду опасность вульгаризации при использовании философских понятий, необходимо корректно формулировать на доступном для учащихся уровне философские выводы при изучении той или иной группы физических явлений.

Например, изучая с учащимися понятие удельной теплоемкости (как, впрочем, и любую другую физическую величину), нельзя начинать с определения физической величины, а следует, как это рекомендуется в различных методических пособиях, с помощью серии экспериментов подвести учащихся к идее об «острой необходимости» введения этой величины, введения не из прихоти учителя, а потому, что опыт говорит о существовании нового свойства вещества, требующего своего описания и количественного выражения. При этом на уроке не следует произносить слова: «Практика - источник знаний. Истина объективна». Сама организация урока должна показать учащимся, что новое знание появляется в результате изучения материального мира, а не «из головы».

Знание учителем философской категории может способствовать выбору рациональной методики формирования физических понятий. Например, если иметь в виду смысл категории взаимодействия (действуют только материальные объекты, действия взаимны, изменения происходят с самими материальными объектами), то становится понятно, почему не стоит при изучении механики вводить составляющие силы, различные скатывающие силы и пр. Ведь если мы хотим, чтобы при изучении механики у уча­щихся формировалось представление о категории взаимодействия, необходимо добиваться понимания ими того, что каждая сила - характеристика действия одного тела на другое. А разве можно для силы, «скатывающей» тело с наклонной плоскости, указать тело, со стороны которого она действует?

Опираясь на знание категории «взаимодействие», учитель должен продумать и методику формирования понятия взаимодействия у учащихся при изучении следующих за механикой разделов курса. Ведь изучаемыми материальными объектами могут выступать не только макротела, как в механике, но и микротела - в молекулярной физике, и тела и поля - в электродинамике. Рассматривая молекулярные, электромагнитные явления, учитель должен показать учащимся, что при взаимодействии изменяются оба материальных объекта.

Методологическое осмысление учебного материала поможет учителю правильно формулировать вопросы к учащимся и не огорчаться, если в ответ произносится вовсе не то, что он ожидал. Например, на вопрос типа «Объясни, почему ...» может последо­вать, по крайней мере, три типа ответов: ученик либо укажет при­чину рассматриваемого явления, либо раскроет его микромеханизм, либо сведет данное явление к знакомому из предыдущего опыта. Учитель же может ожидать только раскрытия причин явления и на другие ответы реагировать как на неверные. Зная, что выявление причины в физических явлениях требует рассмотрения взаимодействий, приводящих к тому или иному физическому явлению, нельзя, например, спрашивать учащихся о причине явления диффузии и ожидать при этом рассказа о проникновении частиц одного вещества в межмолекулярные промежутки другого. Движение частиц вещества - это микромеханизм явления диффузии, но не его причина, поскольку не может быть взаимодействия между микро- и макроуровнями одного и того же объекта.

Стремление учителя формировать у учащихся понимание важнейшего положения о практике как источнике и критерии истинности знаний поможет учителю ограничить использование на уроке учебного физического эксперимента только в качестве иллюстрации знаний, сообщаемых в готовом виде. Учебный экспе­римент должен выступать средством получения новых знаний (при эмпирическом пути познания) или средством проверки пра­вильности полученных теоретически выводов (при теоретическом пути познания).

Знания учащихся по физике станут более глубокими и осмысленными, если учитель «не забудет» о рассмотрении границ применимости любого физического знания (от теории до закона и каждого отдельного понятия). Это рассмотрение выступает конкретным проявлением на уроках физики внимания к философской проблеме конкретности истины. Если учащиеся с помощью учителя «увидят», как развиваются знания о физических объектах и явлениях не только в истории науки, но и в процессе их изучения физики, то это будет вкладом физики как учебного предмета в формирование у уча­щихся понимания диалектики абсолютной и относительной истин и одновременно поможет собственно усвоению знаний.

В целом деятельность учителя физики по формированию научного мировоззрения учащихся может быть представлена следующим образом.

При подготовке к уроку учитель:

а) проводит анализ учебного материала с методологических позиций;

б) формулирует «мировоззренческую» цель урока с учетом ко­нечных целей формирования мировоззрения (какое именно философское обобщение целесообразно формировать на данном уроке), содержания учебного материала, возрастных возможностей учащихся, закономерностей преобразования знаний в убеждения;

в) конкретизирует содержание учебного материала для данного урока и выбирает методы обучения.

Цель урока должна быть сформулирована так, чтобы можно было подобрать средства для ее достижения и проверить результаты работы. Например, цель урока об удельной теплоемкости, о котором уже шла речь, может быть сформулирована так: «Добиться усвоения учащимися знания того, что необходимость введения понятия удельной теплоемкости обусловлена объективно существующими свойствами вещества».

Цель урока, на котором изучается понятие взаимодействия, можно сформулировать следующим образом: «Формировать убеждение учащихся в том, что взаимодействие в механике приводит к появлению ускорения, т.е. к изменению движения, а не к самому движению, путем создания на уроке ситуации преодоления препятствия, связанного с «аристотелевским» пониманием движения». Цель урока об автоколебаниях, о которых мы также уже говори­ли, может звучать так: «Формировать диалектическое мышление учащихся путем включения их в работу с противоположностями свободы и необходимости на примере изучения автоколебаний».

Цели уроков, связанные с формированием системы обобщен­ных знаний на различных уровнях усвоения, следует отнести к по­знавательным целям уроков; цели, направленные на формирова­ние взглядов и убеждений, - к воспитательным, на развитие диа­лектического мышления учащихся - к развивающим.

В ходе проведения урока учитель:

а) организует в соответствии с целью урока изучение нового материала (или его систематизацию, обобщение и пр.) учащимися. Если поставлена цель добиться усвоения знаний на уровне воспроизведения, то можно ограничиться объяснением материала учителем; если же цель урока включает формирование взглядов и убеждений, можно организовать проблемную беседу, диспут и т.п.;

б) организует самостоятельную познавательную деятельность учащихся на уроке с помощью специальных заданий мировоззренческого характера. Эти задания призваны решать одновре­менно две задачи - включать учащихся в деятельность, в которой проходит формирование их мировоззрения, и помогать учителю проверять результативность своей работы в данном направлении.

Итак, в процессе обучения физике в школе учитель может направить свои усилия на формирование системы знаний, системы взглядов и убеждений учащихся и развитие их диалектического мышления. В этой работе целесообразно учитывать два принципа:

1) вся работа на уроке может быть пронизана идеей формирования мировоззрения учащихся, все виды деятельности учителя и учащихся должны быть подчинены цели формирования мировоззрения, и поэтому нет специально направленной на достижение только этой цели деятельности;

2) в решении поставленной задачи необходимо осуществление единства цели, методов, средств и результата.

Учет первого принципа означает подчинение всех этапов урока по физике задаче формирования мировоззрения в сочетании с умением выделить те этапы и виды деятельности, где данная задача играет ведущую роль по сравнению с другими учебно-воспитательными задачами. Учет второго принципа определяет содержание практической деятельности учителя по формированию мировоззрения учащихся.