Интерферометр Фабри - Перо
При наблюдении σ- линий поперечного эффекта Зеемана можно увидеть, что их расщепление возрастает с увеличением интенсивности магнитного поля. Для измерения этого расщепления в единицах длины волны используется интерферометр Фабри–Перо.
Разрешение эталона Фабри-Перо составляет примерно 400000. Это означает, что может быть зафиксировано изменение длины волны менее 0,002 нм.
Данный эталон состоит из стеклянной пластины из кварца, толщиной в 3 мм, с обеих сторон покрытой частично отражающим слоем (степень отражения 90%, степень пропускания 10%). Предположим, что две частично отражающих плоскости (1) и (2) на рис. 9 находятся друг от друга на расстоянии 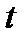 . Входящий луч, образующий угол с перпендикуляром к пластине разделяется на лучи AB, CD, EF и т.д., тогда разность хода лучей между фронтами волны двух соседних лучей (например, AB и CD) равна
. Входящий луч, образующий угол с перпендикуляром к пластине разделяется на лучи AB, CD, EF и т.д., тогда разность хода лучей между фронтами волны двух соседних лучей (например, AB и CD) равна
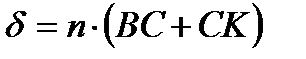 ,
,
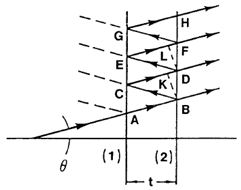
Рис. 9: Отраженные и проходящие лучи в параллельных плоскостях (1) и (2) эталона. Расстояние между пластинами 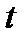 = 3 мм. = 3 мм. |
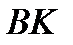 - перпендикуляр к
- перпендикуляр к 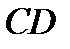 , n - показатель преломления кварца. Для 509 нм n= 1,4519, а для 644 нм n = 1,4560.
, n - показатель преломления кварца. Для 509 нм n= 1,4519, а для 644 нм n = 1,4560. При 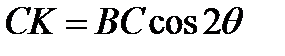 и
и 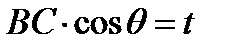
получаем
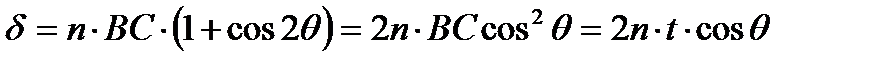
При этом условие усиления интерференции будет
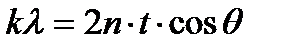 , (3.1)
, (3.1)
где k = 1,2,3¼ порядок спектра, λ - длина волны. Формула (3.1) - основное уравнение интерферометра.
На рис. 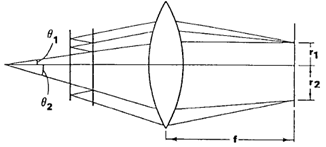
| Рис. 10: Фокусирование световых лучей, выходящих из эталона Фабри-Перо. |
Для малых значений θn, например, лучи проходят почти параллельно оптической оси, удовлетворяющих уравнению (3.1) в фокальной плоскости появляются светлые кольца с радиусом
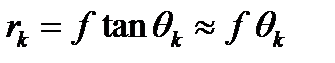 , (3.2)
, (3.2)
где f - фокус линзы.
Поскольку
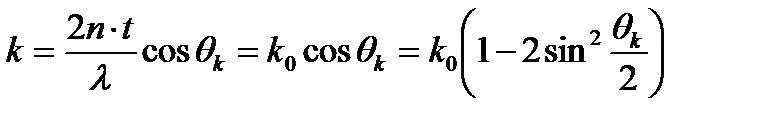
при
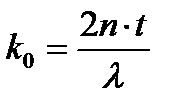
получаем
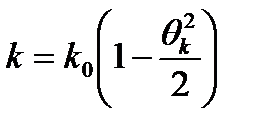
или
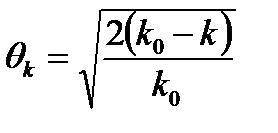 (3.3)
(3.3)
Если 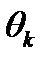 - соответствует светлому краю, k- целое число. Значение
- соответствует светлому краю, k- целое число. Значение 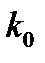 является необходимым условием для интерференции, однако в центре (при θ = 0) k не является целым.
является необходимым условием для интерференции, однако в центре (при θ = 0) k не является целым.
Если 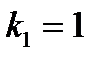 - порядок интерференции для первого кольца,
- порядок интерференции для первого кольца, 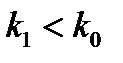 , поскольку
, поскольку 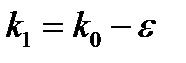 ;
; 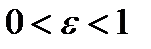 ,
,
где 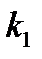 - самое близкое целое число к
- самое близкое целое число к 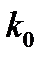 . Для p-го кольца, измеренного от центра, действительно следующее:
. Для p-го кольца, измеренного от центра, действительно следующее:
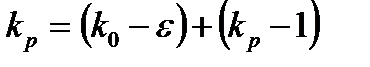 (3.4)
(3.4)
Совместив уравнение (3.4) с уравнениями (3.2) и (3.3), взяв 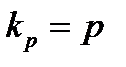 , получим радиусы колец:
, получим радиусы колец:
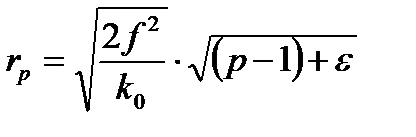 (3.5)
(3.5)
Следует отметить, что разница между квадратами радиусов соседних колец постоянная:
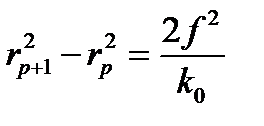 (3.6)
(3.6)
e определяется при построении графика зависимости 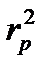 от p и экстраполировании к
от p и экстраполировании к 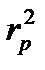 =0.
=0.
Предположим, что существует две линии спектра как результат расщепления одной центральной линии на 2 с длинами волн 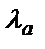 и
и 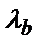 , которые расположены близко друг от друга, то в центре,
, которые расположены близко друг от друга, то в центре, 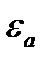 и
и 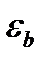 являются дробными числами.
являются дробными числами.
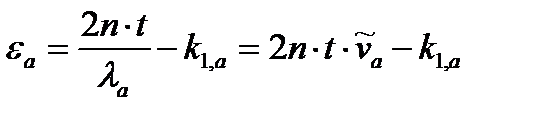
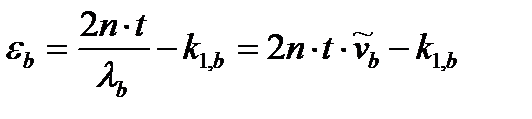 ,
,
где 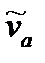 и
и 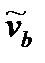 - соответствующие волновые числа, а
- соответствующие волновые числа, а 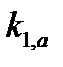 и
и 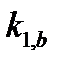 - порядок интерференции первого кольца. Отсюда, если кольца находятся в одном порядке спектра, то
- порядок интерференции первого кольца. Отсюда, если кольца находятся в одном порядке спектра, то 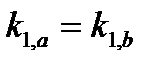 , и разница в волновых числах между двумя компонентами равна
, и разница в волновых числах между двумя компонентами равна
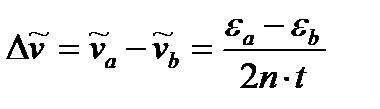 (3.7)
(3.7)
Используя уравнения (3.5) и (3.6), получим
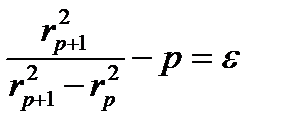 (3.8)
(3.8)
Применив выражение (3.8) к компонентам 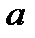 и
и 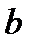 , имеем:
, имеем:
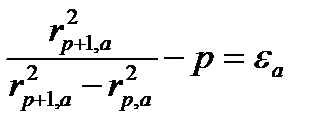
и
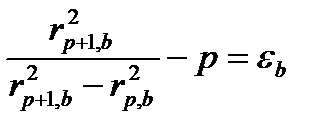
Подставим последние два равенства в уравнение (3.7) и получим разность волновых чисел:
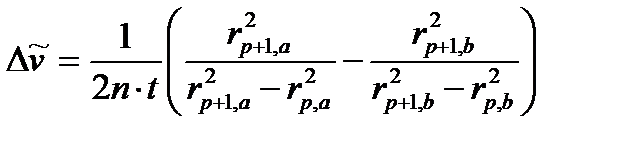 (3.9)
(3.9)
Из выражения (3.6) получаем разницу между квадратами радиусов компонента 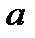 :
:
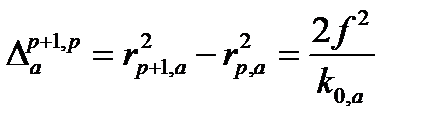 ,
,
что равняется (с небольшим отклонением) значению разницы для компонента 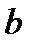 :
:
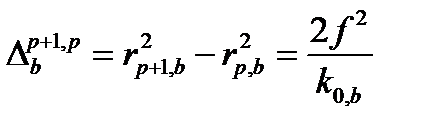
Предположим, что
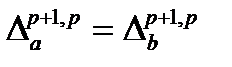
для всех значений 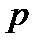 . Аналогично, все значения
. Аналогично, все значения
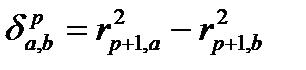
должны быть равны, без учета 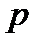 (порядок интерференции). При разнице квадратов радиусов для различных линий одинакового порядка интерференции
(порядок интерференции). При разнице квадратов радиусов для различных линий одинакового порядка интерференции 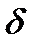 и разнице квадратов радиусов для различных линий различных порядков интерференции Δ как средних значениях получим разницу волновых чисел компонентов
и разнице квадратов радиусов для различных линий различных порядков интерференции Δ как средних значениях получим разницу волновых чисел компонентов 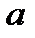 и
и 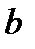 :
:
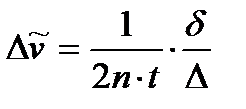 (3.10)
(3.10)
Примечание:
Из выражения (3.10) видно, что 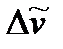 не зависит от измеренных размеров радиусов колец
не зависит от измеренных размеров радиусов колец
