Меры личной профилактики
Все работающие с радиоактивными изотопами должны быть обеспечены индивидуальными средствами защиты (халат, шапочка, перчатки и при необходимости резиновые, хлорвиниловые или клеенчатые фартуки и галоши). Для хранения домашней и специальной одежды должно быть выделено отдельное помещение или специальные шкафы, находящиеся вне рабочих помещений. Специальная одежда должна подвергаться стирке в специальной прачечной не реже одного раза в 10 дней. При переходе из рабочего помещения в другое помещение, где не ведутся работы с радиоактивными изотопами, необходимо обязательно снимать халаты, перчатки и другие средства индивидуальной защиты.
Прием пищи разрешается производить только в специальном помещении, оборудованном умывальником для мытья рук. Следует тщательно мыть руки перед едой, курением и уходом с работы. Рекомендуется троекратное намыливание рук, тщательное растирание с помощью щетки и смывание теплой водой. Ногти всегда должны быть коротко острижены.
При случайном загрязнении тела радиоактивным веществом работающий обязан тщательно вымыться под душем.
Все, работающие с радиоактивными веществами должны не реже одного раза в год проходить медицинский осмотр.
ЗАПРЕЩАЕТСЯ.
1.принимать пищу и хранить пищевые продукты в данных помещениях
2.вносить верхнюю одежду в помещение, где производится работа с радиоактивными изотопами
3.уносить халат домой
4.находиться в рабочих помещениях без халата
5.курить в помещениях, где производятся работы с радиоактивными изотопами.
Лабораторная работа № 1
ИЗУЧЕНИЕ ЗАКОНОМЕРНОСТЕЙ
В СПЕКТРАЛЬНЫХ ЛИНИЯХ ВОДОРОДА
Введение.
Излучение невзаимодействующих друг с другом атомов состоит из отдельных спектральных линий. По этой причине спектр испускания атомов называется линейчатым. Линии в спектрах атомов расположены не беспорядочно, а объединяются в группы – серии линий. Отчетливее всего это обнаруживается в спектре простейшего атома – водорода. На рис. 1. представлена часть спектра атомарного водорода в видимой и близкой ультрафиолетовой области.
| Hα |
| Hβ |
| Hg |
| Hδ |
| H∞ |
| Рис.1. Спектр атомарного водорода в видимой и близкой ультрафиолетовой части спектра. |
| λ |
Символами Hα, Hβ, Hg, Hδ обозначены видимые линии, H∞ указывает границу серии.
Швейцарский физик Бальмер в 1885 году обнаружил, что длины волн этой серии могут быть точно представлены формулой:
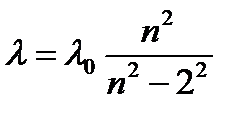 (1.1)
(1.1)
где λ0 – константа, n – целое число, принимающее значения n=3,4,5,…
В спектроскопии предпочитают пользоваться не длиной волны l, а так называемым волновым числом 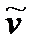 – величиной обратной длине волны, т.е.
– величиной обратной длине волны, т.е.
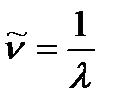 . (1.2)
. (1.2)
В таком представлении можно привести формулу Бальмера к более наглядному виду, в котором ею обычно пользуются в настоящее время. Из равенства (1.1) следует
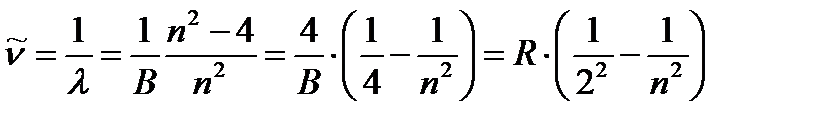 . (1.3)
. (1.3)
Постоянная R= 109677 см-1, одинаковая для всех линий и получившая название постоянной Ридберга, в честь известного шведского спектроскописта Ридберга. Из уравнения (1.3) следует, что при n®¥ линии сгущаются и приближаются к некоторому пределу. Это соответствует действительности.
Затем были исследованы другие участки спектра водорода. Оказалось, что имеется группа линий, лежащих в далеком ультрафиолете, удовлетворяющей формуле
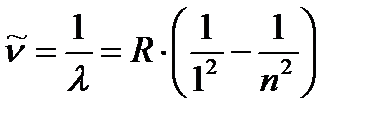 , (1.4)
, (1.4)
где n = 2, 3, 4, 5,¼. Эта группа линий была открыта Т. Лайманом в 1906 г и получила название серии Лаймана. Впоследствии были найдены серии в инфракрасной области.
Серия Пашена (1908 г).
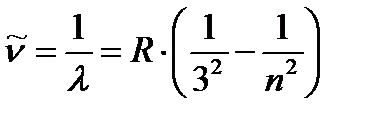 , где n = 4, 5, 6, 7,¼. (1.5)
, где n = 4, 5, 6, 7,¼. (1.5)
Серия Брэкета (1922 г).
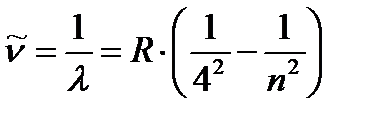 , где n = 5, 6, 7, 8,¼. (1.6)
, где n = 5, 6, 7, 8,¼. (1.6)
Серия Пфунда (1926 г).
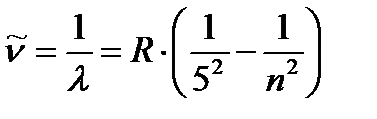 , где n =6, 7, 8, 9,¼. (1.7)
, где n =6, 7, 8, 9,¼. (1.7)
Все серии атома водорода могут быть описаны одной формулой:
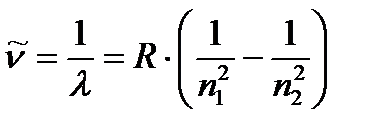 , (1.8)
, (1.8)
где n2 > n1 – целые числа и n1 = Const для данной серии. Это выражение часто называют обобщенной формулой Бальмера.
Из равенства (1.3) для серии Бальмера следует
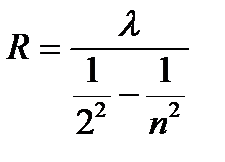 , где n = 2, 3, 4,¼ (1.9)
, где n = 2, 3, 4,¼ (1.9)
2 Теория Бора атома водорода.
Теория Бора атома водорода опирается на следующие основные положения:
планетарную модель атома;
законы классической физики;
постулаты Бора.
Анализируя спектральные закономерности, Бор понял, комбинационный принцип указывает на возможность атома изменять энергию не любым образом, а только дискретно.
Как это следует из его второго постулата, атом, переходя из одного стационарного состояния En2, в другое с меньшей энергией En1 уменьшает свою энергию на величину равную разности энергий этих состояний. Такой переход в частном случае может произойти путем излучения фотона, энергия которого равна hv. Закон сохранения энергии для такого процесса будет иметь вид
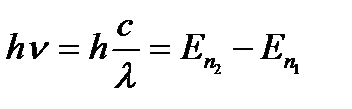 . (2.1)
. (2.1)
 Из (2.1) следует, что частоты линий в спектре определяются полными энергиями атома в различных состояниях. Для планетарной модели, в которой электрон вращается вокруг неподвижного ядра водородоподобного атома, полная энергия атома складывается из кинетической энергии движения электрона и его потенциальной энергии взаимодействия с ядром атома
Из (2.1) следует, что частоты линий в спектре определяются полными энергиями атома в различных состояниях. Для планетарной модели, в которой электрон вращается вокруг неподвижного ядра водородоподобного атома, полная энергия атома складывается из кинетической энергии движения электрона и его потенциальной энергии взаимодействия с ядром атома
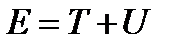 . (2.2)
. (2.2)
Потенциальная энергия в свою очередь определяется кулоновским притяжением электрона к ядру (см. рис. 2), и если предположить, что эта энергия при бесконечно большом расстоянии между ними равна нулю, то на расстоянии r она будет отрицательной и равна[1]
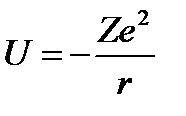 . (2.3)
. (2.3)
В таком случае для полной энергии можно записать
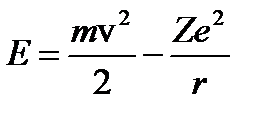 (2.4)
(2.4)
Запишем второй закон Ньютона для равномерного движения электрона по окружности с центростремительным ускорением под действием силы кулоновского притяжения
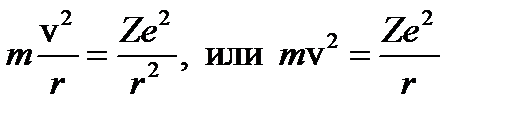 . (2.5)
. (2.5)
Из равенств (2.4) и (2.5) следует
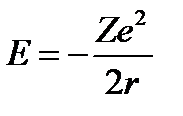 , (2.6)
, (2.6)
что полная энергия атома определяется только радиусом круговой орбиты электрона.
Для того чтобы объяснить устойчивость экспериментально установленной Резерфордом планетарной модели атома, Бор допустил, что внутриатомное движение не во всем следует законам классической физики. Своеобразие атомного движения по Бору проявляется в том, что могут иметь место движения заряженной частицы по замкнутым орбитам, которые вопреки законам классической электродинамики не будут сопровождаться излучением энергии. Эту мысль Бор выразил в другой формулировке своего первого постулата: «Из бесконечного числа электронных орбит, возможных с точки зрения классической физики, осуществляются только некоторые стационарные орбиты, двигаясь по которым электрон вопреки классической электродинамике не излучает энергии». При этом правило отбора разрешенных орбит Бор формулирует следующим образом: «Разрешены только те орбиты, для которых момент импульса электрона кратен постоянной Планка ħ». Если представить замкнутую орбиту в виде окружности, то согласно правилу отбора можно записать
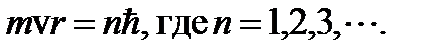 (2.7)
(2.7)
Последнее правило в виде (2.7) было постулировано Бором, но его можно легко получить исходя из волновых свойств электрона. Действительно, если электрон, двигаясь по стационарной орбите, не излучает энергию, то с волновой точки зрения фаза дебройлевской волны, с которой электрон, сделав полный оборот, придет в некоторую точку круговой орбиты, должна быть такой же, с какой он вышел из этой точки. Иными словами на всю длину орбиты должно укладываться целое число (кроме нуля) волн де Бройля
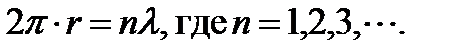
Так как
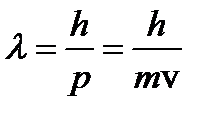 ,
,
то
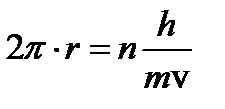 ,
,
или
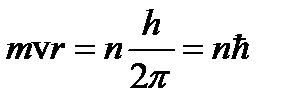
Из совместного решения равенств (2.5) и (2.7) вытекают два важных соотношения
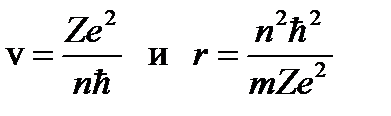 , (2.8)
, (2.8)
которые говорят о том, что скорость и радиус движения электрона квантуются, т.е. могут принимать лишь только определенные дискретные значения. При этом наименьший радиус электрона в атоме водорода (n=1 и Z=1) равен константе
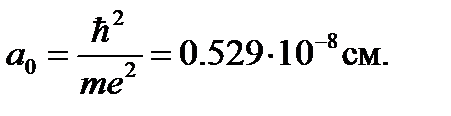 , (2.9)
, (2.9)
которая получила название радиуса первой боровской орбиты. Тогда радиусы других орбит будут равняться
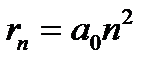 . (2.10)
. (2.10)
Подставим в выражение (2.6) радиусы разрешенных орбит, определяемые соотношением (2.8)
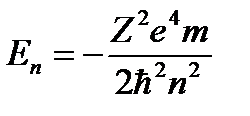 . (2.11)
. (2.11)
В таком случае равенство (2.1) принимает вид
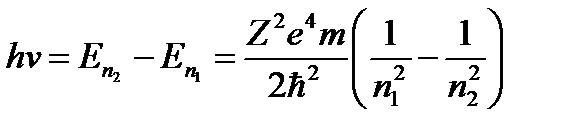 . (2.12)
. (2.12)
Так как
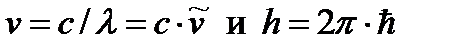 , (2.13)
, (2.13)
то
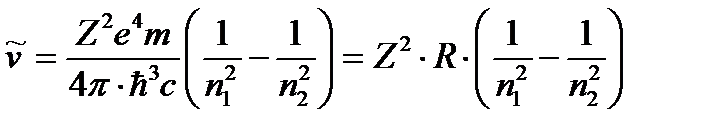 , (2.14)
, (2.14)
где 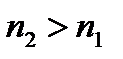 - целые числа и константа
- целые числа и константа 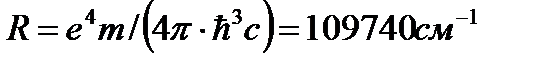 .
.
Так как для атома водорода Z=1, то последняя формула (2.14) полностью совпадает с обобщенной формулой Бальмера (1.8).
Если учесть, что в действительности ядро не покоится, а движется вместе с электроном вокруг общего центра масс (смотри лабораторную работу «Изотопический сдвиг»), то эта константа будет равна 109677см-1, т.е. в точности совпадает с постоянной Ридберга.
Таким образом, получается превосходное согласие теории с опытом, для случая атома водорода.
Недостатки теории Бора.
Как установили выше, теория Бора достигла больших успехов в обосновании атомной спектроскопии; она явилась крупным шагом в развитии теории строения атома. Ее огромное значение в развитии физики заключается, прежде всего, в том, что она с полной очевидностью показала неприменимость классических представлений к внутриатомным явлениям, показала роль квантовых законов в мире микрочастиц. Она объяснила ряд явлений, послужила толчком к огромному числу работ, установивших ряд важных экспериментальных фактов.
Однако наряду с этими достоинствами теория Бора обладает рядом серьезных недостатков, многие из которых обнаружили сразу же, а другие вскрылись в процессе развития атомной физики. Одним из недостатков, который выяснился на самой ранней стадии развития боровской теории, явилась безуспешность попыток построения теории атома гелия – одного из простейших атомов периодической системы. Произведенные расчеты возможных энергетических уровней атома гелия находились в резком противоречии с результатами опыта. В простейшем случае водородоподобных атомов теория Бора позволяла вычислять только частоту спектральных линий и не давала аппарата для расчета их интенсивностей. К числу недостатков теории Бора следует отнести ее внутреннюю противоречивость. По этому поводу Брэгг заметил: «В этой теории мы как бы должны по понедельникам, средам, пятницам пользоваться классическими законами, а по вторникам, четвергам, субботам – квантовыми». Спустя 15 лет после того, как Бор сформулировал свою теорию, стало ясно, что эта теория, опирающаяся на классическую механику и квантовые закономерности излучения одновременно, но не учитывающая волновых свойств частиц, в принципе не могла быть последовательной теорией атомных процессов, а явилась только переходным этапом к разработке такой теории.
3. Экспериментальная часть
Цель работы.
Исследование серии Бальмера спектра атома водорода с помощью дифракционной решетки. Определение энергетических уровней и постоянной Ридберга.
Оборудование.
Спектральная трубка с водородом 06665.00
Спектральная трубка с ртутью 06664.00
Пара держателей для трубки 06674.00
Защитная трубка 06675.00
Кабель, 30 кВ, 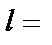 1000 мм, 2 шт. 07367.00
1000 мм, 2 шт. 07367.00
Держатель объекта, 5х5 см 08041.00
Дифракционная решетка, 600 штр./мм 08546.00
Источник высокого напряжения, 0-10 кВ 13670.93
Изолирующий держатель, 2 шт. 06020.00
Треножник 02002.55
Подставка 02006.55
Стержень 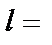 40 см 02026.55
40 см 02026.55
Метровая шкала 03001.00
Пара курсоров 02201.00
Измерительная лента 09936.00
Выполнение работы.
Соберите установку, как показано на рисунке 3.
Рис. 3. Экспериментальная установка для наблюдения спектра атома водорода
В качестве источника излучения используются трубки с водородом и с ртутью, на которые для зажигания подается высокое напряжение от источника (2-4 кВ). Шкала должна быть расположена сразу за трубкой. Дифракционная решетка устанавливается параллельно шкале на одной высоте со спектральной трубкой. Расстояние между решеткой и трубкой устанавливается таким, чтобы наблюдаемая дифракционная картина была четкой (примерно 50 см). Наблюдения дифракционной картины следует проводить в затемненной комнате, смотря через решетку на спектральную трубку.
При падении света длиной волны λ на дифракционную решетку с постоянной решетки D можно наблюдать дифракционную картину. Максимумы интерференции наблюдаются для углов дифракции α, определяемых соотношением:
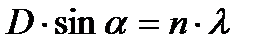
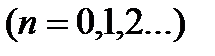 (3.1)
(3.1)
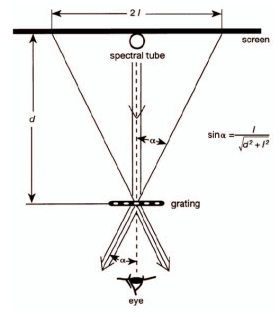
| Рис. 4. Ход лучей при дифракции на дифракционной решетке |
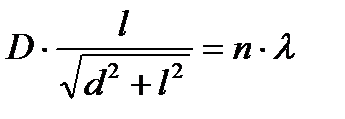 , (3.2)
, (3.2)
где d - расстояние от решетки до экрана, l- половина расстояния между двумя дифракционными линиями одной длины волны и одного порядка дифракции.
Задание 1. Определение постоянной решетки с помощью спектра атомов ртути.
Установите спектральную трубку с ртутью. Включите источник напряжения. Подавая высокое напряжение на трубку, получите ее зажигание. Наблюдайте спектр атомов ртути. Измерьте расстояние d между решеткой и трубкой.
Для трех видимых спектральных линий (желтая 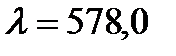 нм, зеленая
нм, зеленая 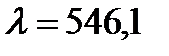 нм и синяя
нм и синяя 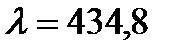 нм) в первом порядке дифракции измерьте по шкале расстояние
нм) в первом порядке дифракции измерьте по шкале расстояние 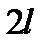 - расстояние между одинаковыми по цвету линиями (используйте для этого курсоры). Заполните таблицу 1. Выключите источник высокого напряжения.
- расстояние между одинаковыми по цвету линиями (используйте для этого курсоры). Заполните таблицу 1. Выключите источник высокого напряжения.
Таблица 1.
| Цвет линии | 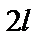 , мм , мм | 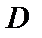 , мкм , мкм |
Вычислите постоянную решетки по формуле (5). Определите ее среднее значение и оцените погрешность.
Задание 2. Определение длин волн линий серии Бальмера для атома водорода. Вычисление постоянной Ридберга и энергий атомных уровней.
Установите спектральную трубку с водородом. Включите источник напряжения. Подавая высокое напряжение на трубку, получите ее зажигание. Наблюдайте спектр атомов водорода. Измерьте расстояние d между решеткой и трубкой.
Для трех-четырех видимых спектральных линий в первом порядке дифракции измерьте по шкале расстояние 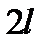 - расстояние между одинаковыми по цвету линиями (используйте для этого курсоры). Заполните таблицу 2. Выключите источник высокого напряжения.
- расстояние между одинаковыми по цвету линиями (используйте для этого курсоры). Заполните таблицу 2. Выключите источник высокого напряжения.
Таблица 2.
| Линия (см. рис. 1) | 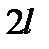 , мм , мм | 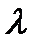 , нм , нм | 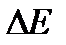 , эВ , эВ | 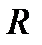 , м-1 , м-1 |
Вычислите длины волн 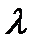 (формула (3.2), значение постоянной решетки определяется в задании 1), разность энергий атомных уровней ΔE (формула (2.1)), постоянную Ридберга R (формула (1.9)). Определите среднее значение постоянной Ридберга, сравните ее с теоретическим значением.
(формула (3.2), значение постоянной решетки определяется в задании 1), разность энергий атомных уровней ΔE (формула (2.1)), постоянную Ридберга R (формула (1.9)). Определите среднее значение постоянной Ридберга, сравните ее с теоретическим значением.
Используя данные рисунка 5, и полученные значения ΔE вычислите значения энергий атомных уровней с n =3, 4, 5. Сравните их с теоретическими значениями.
На рисунке 5 показана диаграмма энергетических уровней и спектральных серий атома водорода.
Рис. 5. Диаграмма энергетических уровней атома водорода:
Отчет по работе должен содержать.
1. Цель работы.
2. Краткую теорию Бора.
3. Описание установки согласно рис. 1.
4. Результаты измерений (таблицы).
5. Теоретические расчеты.
6. Сравнение расчетных и экспериментальных данных и определение ошибки.
7. Вывод.
Вопросы к отчету
1. Сформулируйте постулаты Бора.
2. *Получите формулу (2), исходя из модели атома водорода по Бору.
3. *Получите формулу (3), исходя из модели атома водорода по Бору.
4. Что называется, серией Бальмера?
5. Что такое энергия связи?
6. Что называют постоянной дифракционной решетки?
7. Напишите и поясните уравнение максимумов интерференции для дифракционной решетки.
Литература
1. Техническая документация и методические указания немецкой фирмы PHYWE (на английском языке).
2. Шпольский Э.В. Атомная физика. Т. 1. М., Наука, 1974.
3. Сивухин Д.В. Общий курс физики. Т. V-1. М., Наука, 1986.
4. Методические пособия к лабораторным работам по курсу «Физический практикум (Атомная физика)».
