Уравнение первого закона термодинамики для потока газа

Ранее было показано, что dq = di – vdP. Т.к. 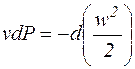, то

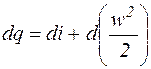. (9.8)

Из этого уравнения видно, что теплота dq, подведенная к элементарной массе потока, идет на увеличение его энтальпии diи кинетической энергии, которую можно превратить в механическую работу. При адиабатном течении газа dq = 0, и для этого случая:

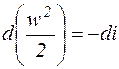, (9.9)

т.е. сумма удельной энтальпии и удельной кинетической энергии сохраняет постоянное значение. Последнее уравнение справедливо как для обратимых, так и для необратимых течений. Если газ при течении по каналу совершает техническую работу l_тех, то уравнение первого закона имеет вид:

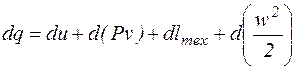, или

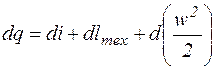. (9.10)

При адиабатном течении газа dq = 0, отсюда:

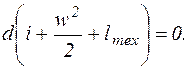(9.11)

После интегрирования:

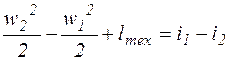. (9.12)

Располагаемая работа газа в потоке

Ранее было показано, l₀ – располагаемая работа равна: l₀ = -vdP, но 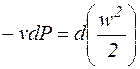, т.е. располагаемая работа l₀при течении газа равна его кинетической энергии:

l₀ = 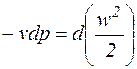. (9.13)

Из уравнения видно, что при обратимом процессе увеличение скорости w связано с уменьшением давления, и наоборот, уменьшение скорости сопровождается повышением давления.

Сопла – это каналы, в которых происходит расширение газа с уменьшением давления (dP< 0) и увеличением скорости (dw > 0).

Диффузоры - это каналы, в которых происходит сжатие газа с увеличением давления (dP > 0) и уменьшением скорости (d w < 0).

Из последнего уравнения видно, что необходимым условием получения располагаемой работы является уменьшение давления, т.к. при dP< 0, dl₀ > 0. Если dP= 0 (в течение процесса давление постоянное), то располагаемая работа равна нулю.

Как известно, располагаемая работа l₀ зависит от вида процесса. Причем располагаемая работа может быть больше, меньше работы расширения или равна ей.

Для адиабатного процесса расширения газа l₀ = kl, или

.

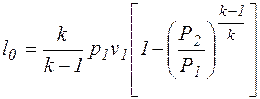Для адиабатного течения газа располагаемая работа может быть определена через энтальпию. Т.к.

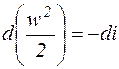, а

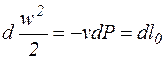, то 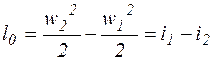. (9.14)

Следовательно, располагаемая работа газа при адиабатном течении равна разности энтальпий в начальном и конечном состояниях.

Уравнение неразрывности

Рассмотрим движение потока газа через трубу переменного сечения (рис. 9.3). Если течение газа установившееся, то через любое произвольное поперечное сечение трубы в единицу времени протекает одна и та же масса газа.

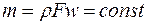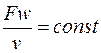, или и 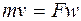, где (9.15)

r- плотность; F – площадь поперечного сечения трубы; w - скорость; v – удельный объем.

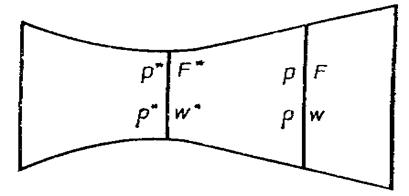
Рис. 9.3. К выводу уравнения неразрывности

Уравнение 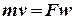называется уравнением неразрывности или сплошности потока. Данное уравнение устанавливает связь между площадью проходного сечения канала и скоростью потока. Для несжимаемого потока газа r = const, поэтому wF= const, т.е. с увеличением поперечного сечения трубы скорость wубывает и наоборот.

Значительно сложнее течение сжимаемого газа. В этом случае профиль сопла при данном расходе газа m = constбудет зависеть не только от характера изменения скорости w, но и от плотности r (удельного объема v), который изменяется по закону адиабаты.

Логарифмируя и дифференцируя уравнение сплошности (при m = const) получаем:

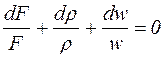
Это уравнение неразрывности в дифференциальной форме, которое с помощью уравнения Бернулли может быть приведено к форме

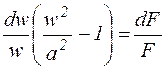, или 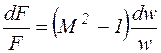, (9.16)

где а – местная скорость звука.

Отношение скорости газа wк местной скорости звука а в этом же сечении канала

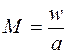
называют числом Маха. Различают дозвуковую и сверхзвуковую скорости газа. При М > 1- сверхзвуковая, при М < 1 - дозвуковая скорости течения.

Скорость истечения

Чтобы найти скорость истечения газа через сопло, нужно проинтегрировать уравнение:

; ,

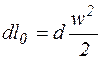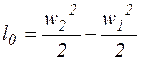где w ₁ и w ₂ – значения скорости в конце и начале процесса.

Для случаев, когда , w ₂ >> w ₁, то членом w₁ можно пренебречь, получаем:

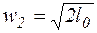, (9.17)

но т.к. l₀ связано с параметрами 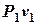, можно записать:

,

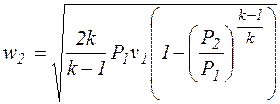или

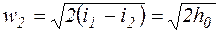(9.18)

Из последних формул видно, что скорость истечения определяется параметрами газа 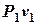на входе в сопло и его давлением P₂ на выходе, или разностью энтальпий h₀ на входе и выходе из сопла.

При истечении газа в вакуум (P₂ = 0) скорость истечения будет максимальная.

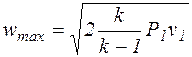. (9.19)