Определение термического КПД цикла через среднеинтегральные температуры
Термический КПД произвольного цикла может быть определен через среднеинтегральные температуры по формуле:

 , (6.19)
, (6.19)
где  - среднеинтегральная температура подвода теплоты в процессе.
- среднеинтегральная температура подвода теплоты в процессе.
Т.е. термический КПД произвольного цикла равен термическому КПД цикла Карно, осуществляемому между среднеинтегральными температурами процессов подвода (  ) и отвода (
) и отвода (  ) теплоты. На рис. 6.4. приведены обратимые циклы А, B, C и D, которые имеют одинаковые максимальную
) теплоты. На рис. 6.4. приведены обратимые циклы А, B, C и D, которые имеют одинаковые максимальную  и минимальную
и минимальную  температуры. Из рисунка видно, что
температуры. Из рисунка видно, что  >
>  >
>  >
>  и
и  <
<  <
<  <
<  . Поэтому
. Поэтому  >
>  >
>  >
>  .
.

Рис. 6.4. К определению термической КПД цикла.
Методы сравнения термических КПД обратимых циклов
Обычно сравнение циклов производится в sT-диаграмме двумя способами.
При сравнении первым способом основным критерием является коэффициент заполнения, равный отношению площади рассматриваемого произвольного цикла (пл. abcd на рис. 6.5,а) к площади цикла Карно, осуществляемого в том же интервале температур и энтропий, т.е. к пл. 1234. Любой произвольный цикл, вписанный в цикл Карно, имеет площадь, меньшую, чем площадь цикла Карно. Из двух циклов, осуществляемых в одном и том же интервале температур, большее значение 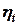 имеет тот цикл, у которого выше коэффициент заполнения.
имеет тот цикл, у которого выше коэффициент заполнения.
Второй способ основан на понятиях среднеинтегральных температур подвода и отвода теплоты в циклах и предполагает замену рассматриваемого произвольного цикла тепловой машины эквивалентным циклом Карно с температурами  и
и  . Чем выше среднеинтегральная температура подвода теплоты
. Чем выше среднеинтегральная температура подвода теплоты  и чем ниже среднеинтегральная температура отвода теплоты
и чем ниже среднеинтегральная температура отвода теплоты  , тем выше
, тем выше 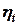 произвольного цикла (рис. 6.5,б).
произвольного цикла (рис. 6.5,б).

Рис. 6.5 К методу сравнения термической КПД.
Обобщенный цикл Карно
Теоретически любой обратимый цикл, например, abfe (рис. 6.6), в котором подвод и отвод теплоты производится по изотермам, может быть равнозначен по термодинамической эффективности обратимому циклу Карно abcd. В этом случае адиабаты расширения и сжатия цикла Карно должны быть заменены произвольными обратимыми процессами bfи ea, единственным условием изображения является эквидистантность в горизонтальном направлении. Эти процессы протекают в интервале температур Т1-Т2. Для осуществления обратимого теплообмена в процессе bfпри охлаждении рабочего тела от Т1 до Т2 необходимо иметь неограниченное количество промежуточных точечных приемниковтеплоты, температура которых отличается друг от друга на малую величину. Для осуществления обратимого теплообмена в процессе еапри нагревании рабочего тела от Т1 до Т2 необходимо иметь неограниченное количество промежуточных точечных источников теплоты. Вследствие эквидистантности линий bfи еа, количество теплоты, отданное рабочим телом в процессе bf(площадь f bb'f'), равно количеству теплоты, полученному рабочим телом в процессе еа (площадь еаа'е'). Таким образом, в цикле осуществляется полная регенерация теплоты.
Приемники теплоты для процесса bf и источники теплоты для процесса еамогут быть сосредоточены в едином устройстве, называемом идеальным регенератором. В качестве идеального регенератора может быть использована труба бесконечно большой теплоемкости, на концах которой поддерживаются температуры Т1 и Т2.

Рис. 6.6. Обобщенный (регенеративный) цикл Карно
После получения теплоты q1 от внешнего источника рабочее тело направляется в регенератор, где по линии bfему передается часть теплоты. На участке fе рабочее тело при Т2 = const отдает теплоту q2 внешнему приемнику, а затем движется через регенератор в обратном направлении и по линии еа получает от него теплоту. Линия подвода теплоты аb у цикла abfeи цикла Карно общая, поэтому q1 для них одинаково. Одинаковы по величине и линии процессов отвода теплоты fe и сd, поэтому q2 для них тоже одинаково. Следовательно, в соответствии с выражениями для термического КПД, термический КПД для обоих циклов:  , т.е. термический КПД рассмотренного обратимого цикла равен термическому КПД цикла Карно.
, т.е. термический КПД рассмотренного обратимого цикла равен термическому КПД цикла Карно.
Цикл, в котором принимают участие регенераторы теплоты, называется регенеративным циклом.
Обратимый регенеративный цикл, состоящий из двух изотерм и двух любых произвольных эквидистантных кривых, называется обобщенным регенеративным циклом Карно.
7. ВОДЯНОЙ ПАР
