Г- фазовый объем некоторой области такого пространства

Основной статистической характеристикой ансамбля частиц является функция распределения частиц в фазовом пространстве.

Функция распределения есть плотность частиц в фазовом пространстве.

(2.3.2)

Число частиц в элементе фазового объема определится, как:

. (2.3.3)

Интересующие нас явления и процессы обычно представляют собой результат суммарного действия большого числа частиц. Поэтому наблюдаемые параметры представляются интегралами от функций распределения :

Плотность частиц

(2.3.4)

Полное число частиц в системе

(2.3.5)

Локальная плотность потока частиц.

(2.3.6)

Энергосодержание в единице объема — давление

(2.3.7)

Плотность потока энергии.

(2.3.8)

2.3.2. Кинетическое уравнение без столкновений

Кинетическое уравнение это уравнение, описывающее поведение ансамбля частиц в фазовом пространстве. При отсутствии столкновений оно представляет собой аналог уравнения непрерывности, модифицированного под фазовое пространство. Именно, если функция распределения f в фазовом пространстве является аналогом распределения плотности частиц n в обычном пространстве

(x, y, z,t) ( , t)

то можно продолжить цепочку аналогий:

Последнее уравнение в правом столбце преобразуется

(2.3.9)

Если r, u — независимые переменные и не зависит от скорости (силы не диссипативные ), то

(2.3.10)

Выписанное выше уравнение и является бесстолкновительным кинетическим уравнением.

2.3.3. Самосогласованное поле и уравнение Власова.

Самое простое, что можно сделать для описания взаимодействия между частицами в плазме, это вычислить силу по средним значениям функции распределения. При этом можно найти функцию распределения частиц, при которой создается силовое поле, поддерживающее это распределение. Кинетическое уравнение в этом случае выглядит следующим образом

(2.3.11)

Оно было предложено впервые Власовым, и поэтому называется уравнением Власова. Значения напряженностей электрического и магнитного полей вычисляются с использованием системы уравнений Максвелла, в которую вставляются значения плотностей зарядов и токов, полученные с использованием функций распределения частиц:

(2.3.12)

Полученная система уравнений дополняется граничными и начальными условиями и является математической моделью, описывающей так называемую бесстолкновительную плазму. Эта модель хорошо работает при исследовании процессов, характерные времена развития которых, значительно меньше времен столкновений между частицами плазмы.

2.3.4. Учет столкновений.

Если нас интересуют процессы, характерные времена развития которых сравнимы или превышают столкновительные, кинетическое уравнение должно быть дополнено членом, учитывающим столкновения.

Кинетическое уравнение Больцмана

Запишем полученное выше уравнение (2.3.10), добавив в правую часть дополнительный член, учитывающий быстро флуктуирующие поля и силы, возникающие при сильном сближении частиц :

(2.3.13)

Это кинетическое уравнение Больцмана. Индекс а обозначает сорт частиц, а индекс α – координату (x, y, z). Таким образом, эта сокращенная запись подразумевает на самом деле систему стольких уравнений, сколько видов частиц имеется в плазме.

Конкретный вид столкновительного члена может быть различным для разных типов столкновений. Для неупругих столкновений он не всегда вообще может быть записан в явном виде. Частицы сорта а, для которых записано уравнение, могут сталкиваться друг с другом и с частицами других сортов. Поэтому, вообще говоря.

(2.3.14)

St_ав дает изменения в единицу времени в результате столкновений с частицами сорта в.

Некоторые свойства столкновительного члена можно указать, не зная его явного вида. Если не учитывать процессы, превращающие частицы из одного сорта в другой, например – ионизацию, то:

(2.3.15)

Действительно, первый из интегралов, умноженный на , дает изменения числа частиц сорта а в элементе объема ,, в результате столкновения с частицами в. Но при упругих столкновения такого изменения нет.

Два других интеграла дают изменения соответственного импульса, и энергии частиц сорта а , из-за столкновений между собой . Но так как при упругих столкновениях импульс и энергия сохраняются, то они также равны нулю.

Аналогично можно записать суммарные законы сохранения импульса и энергии для частиц сорта а и в

(2.3.16)

Уравнения для макроскопических параметров, называемые обычно уравнениями переноса, можно получить из кинетического уравнения. Просто, интегрируя его по скоростям с учетом первого из уравнений (2.3.15), получим уравнение непрерывности. Если перед интегрированием умножить его на или на , то получим соответственно уравнения переноса импульса и энергии.

Интеграл столкновений.

Наиболее простой вид интеграла столкновений может быть задан формулой:

(2.3.17)

Это интеграл столкновений Батнагара – Гросса - Крука (так называемое БГК – приближение, или t -приближение). При этом сохраняется число частиц, но не сохраняется импульс, что является недостатком приближения (преимущество – простота!). Такой подход является полуфеноменологическим подходом к исследованию кинетических процессов: выражение (2.3.17) постулирует установление равновесной функции распределения ( к которой стремится любая 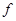) с помощью столкновений за характерное время, порядка t. Приближение позволяет в ряде случаев получать удовлетворительные результаты. Например, использовав t- приближение кинетического уравнения для электронов, можно получить формулу электропроводности. Рассмотрим постоянный ток в однородной плазме. Кинетическое уравнение в этом случае будет иметь вид:

(2.3.18)

Пусть 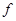слабо отличается от , где -малая добавка, что может быть справедливым при достаточно малом электрическом поле. Тогда:

(2.3.19)

т.к произведением двух малых сомножителей можно пренебречь. Из ( 2.3.18) следует (считаем скорость направленной в направлении электрического поля):

,

и плотность тока может быть вычислена следующим образом

(2.3.20)

Здесь применено интегрирование по частям:

; [т.к. ]

Уточним смысл требования слабого электрического поля: означает в соответствии с выражением (2.3.18) и с учетом того, что

или (2.3.21)

Это означает, что энергия, приобретаемая электроном в электрическом поле на длине свободного пробега должна быть существенно меньше тепловой.

Как будет показано далее, особенностью кулоновских столкновений является относительно большой вклад далеких пролетов, приводящий к большому числу отклонений рассеиваемых частиц на малые углы. Это особенность дает возможность записать столкновительный интеграл в диффузионном приближении, с учетом рассеивания частиц лишь на очень малые углы . Такая форма интеграла столкновений была предложена впервые Л.Д. Ландау . Основная идея Ландау заключается в том ,что поток частиц в пространстве скоростей представляется в виде двух членов , первый из которых обусловлен силой динамического трения

, (2.3.22)

где - частота столкновений, а второй – процессом диффузии частиц. Для одномерного случая это представление выглядит следующим образом:

(2.3.23)

Как было сказано ранее, интеграл столкновений должен обратиться в нуль при равновесной функции распределения 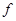, т.е. в термодинамическом случае совпадающей с максвелловской

(2.3.24)

Подставляя (2.3.24) в (2.3.23) и требуя обращения последнего в нуль, получаем

; откуда

и, следовательно, (2.3.25)

Окончательно столкновительный интеграл примет следующий вид:

(2.3.26)

Полученный результат обобщается на трехмерный случай с учетом того, что тензор коэффициентов диффузии.

(2.3.27)

При этом:

(2.3.28)

В некоторых случаях составляющей динамического трения можно пренебречь. Тогда достаточно в интеграле столкновений оставить только чисто диффузионный член со второй производной. Это хорошо описывает сильно неравновесную ситуацию, когда в плазме под действием каких либо внешних причин возникает в некоторой области пространства скоростей сильный градиент функции распределения. Вид столкновительного интеграла в таком случае следующий:

(2.3.29)

это также дает полуфеноменологическое, модельное описание установления максвелловского распределения .

Глава 3. Взаимодействие частиц в плазме.

3.1. Основные понятия теории столкновений.

Процесс взаимодействия частиц называется столкновением в том случае, если он происходит за отрезок времени, гораздо более короткий, чем все другие, интересующие нас процессы, и мы не рассматриваем развитие его во времени, а интересуемся только исходным и результирующим состоянием системы. Обычно принимаются в расчет только парные столкновения – во-первых они наиболее вероятны, а во-вторых изучение, скажем, тройного столкновения, вызывает серьезные математические трудности. Считается, что столкновение произошло, если частицы вначале сближались друг с другом, а потом разошлись, причем произошло какое-то физическое изменение в этой системе.

Столкновение называется упругим, если в результате этого столкновения происходит изменение лишь энергии и импульса взаимодействующих частиц. Упругие столкновения приводят к рассеянию, торможению пучков частиц; к охлаждению более горячей и нагреву более холодной компонент плазмы

Столкновение называется неупругим, если в результате этого столкновения происходит изменение внутренней энергии частиц или рождение новых (исчезновение исходных) частиц. Неупругие столкновения соотносятся с процессами возбуждения, ионизации, диссоциации и обратных им изменений состояния взаимодействующих частиц.

Для описания столкновений применяется вероятностный подход. Вероятность

того или иного результата столкновения определяется так называемым эффективным сечением столкновения. Обычно его обозначают греческой буквой s.

Эффективное сечение столкновения s может рассматриваться как величина,

пропорциональная обратной средней длине свободного пробега. В приближении, при котором взаимодействующие частицы моделируются непроницаемыми упругими шариками, средняя длина свободного пробега в однородном газе дается формулой, выведенной Максвеллом:

(3.1.1.)

Здесь n – число атомов или молекул в 1см³ , r – радиус шарика, моделирующего рассматриваемую частицу.

Величина s =pr² , введенная здесь, имеет смысл площади поперечного сечения цилиндра, «заметаемого» модельным шариком. Всякий другой шарик, попадающий полностью или частично внутрь этого цилиндра, испытает столкновения с «пробным» шариком.

Рис. 3.1 Модель твердых сфер в теории столкновений.

Если рассматривать шарики двух сортов (1 и 2), имеющие разные радиусы (r₁ и r₂), то нетрудно показать, что средняя длина свободного пробега частиц сорта 1 в среде частиц сорта 2 выразится формулой

(3.1.2.)

Полное число таких столкновений в 1 секунду

(3.1.3)

Здесь ; .

При столкновениях электронов с атомами газа (частицы сорта 1 – электроны, частицы сорта 2 – атомы) и . При этом (3.1.2.) и (3.1.3) будут выглядеть соответственно:

(3.1.2.а)

(3.1.3а)

Наряду с моделью упругих непроницаемых сфер, применяются и другие модели; главным отличием их друг от друга является форма пространственного распределения потенциала взаимодействия и классичность или квантовость подхода к рассмотрению процесса столкновения.

3.2. Кулоновские столкновения.

Поскольку важнейшим признаком плазмы, является определяющая роль

кулоновского характера взаимодействия частиц, нам следует обратить особое внимание на кулоновские столкновения.

3.2.1. Кулоновский логарифм и особенности кулоновского взаимодействия.

Изучение характеристик этого взаимодействия удобно начать с модельной задачи по расчету силы, действующей на неподвижный «кулоновский центр» со стороны «налетающего» на него плоского потока заряженных частиц.

Пусть имеется точечный заряд e_a , помещенный в точке пространства, принимаемой нами за начало отсчета и закрепленный там неподвижно. Из бесконечности вдоль оси z на него налетает однородный плоский поток частиц с массой m и зарядом e_b. Требуется найти усредненную силу, действующую на этот неподвижный заряд со стороны налетающего потока.

Рис. 3.2.

Рассмотрение будем вести в приближении парных соударений, то - есть будем считать, что в каждый момент с кулоновским центром взаимодействует только одна частица. Решение задачи о рассеянии одной заряженной частицы на неподвижном кулоновском центре хорошо известно еще со времен Резерфорда поэтому мы воспользуемся этим результатом. Рассеиваемая частица движется по гиперболе, и угол рассеяния q связан с прицельным параметром r — расстоянием, на котором частица пролетала бы от силового центра, если бы взаимодействие отсутствовало, соотношением:

(3.2.1)

где r_^ = (q_a q_b )/mu² -значение прицельного параметра, при котором частица отклоняется на прямой угол q = p /2 .Сечение рассеяния вычисляется по формуле Резерфорда.

Результирующая сила, действующая на рассеивающий центр со стороны потока частиц направлена вдоль оси z в связи с однородностью этого потока. По величине она равна силе, действующей в обратном направлении - со стороны рассеивающего центра на поток. Вычислить ее можно, зная изменение суммарного импульса частиц потока в единицу времени

(3.2.2)

Поскольку столкновения считаем упругими, скорость налетающих частиц не меняется по величине : u^’ = u

Рис.3.3.

Изменение проекции каждой частицы на ось zбудет в результате выглядеть следующим образом :

(3.2.3)

Здесь использована связь q и r , даваемая уравнением (3.2.1).

Через элементарную площадку ds =r dr dj за единицу времени проходит число частиц потока n_b u ds . Умножив эту величину на изменение импульса одной частицы Dp_z^b =m Du_z^b и интегрируя по всей плоскости, найдем суммарное изменение импульса потока частиц в единицу времени и, следовательно, силуF:

(3.2.4)

Интеграл, входящий в выражение (3.2.4) логарифмически расходится при r ® µ , что дает физически неприемлемый результат. Чтобы получить конечное значение для силы Fверхний предел интегрирования необходимо ограничить некоторым значением r_max >> r_^ . Тогда, обозначив получающееся значение интеграла через L, получим :

(3.2.5)

Подставив затем в формулы (3.2.4) и (3.2.5) значение r_^ = (q_a q_b )/mU² , имеем

(3.2.6)

где (3.2.7)

так называемый «кулоновский логарифм»; его значение зависит от выбора верхнего предела интегрирования по r . В условиях плазмы за r_max логично выбрать величину дебаевского радиуса, так как именно эта величина является характерным пространственным масштабом , определяющим расстояние, на котором происходит резкое ослабление поля точечного заряда.

Таким образом в плазменных условиях имеем следующее выражение для кулоновского логарифма :

(3.2.8)

(при и T_e = 10 кэВ, ; при и T_e = 100 эВ,

В теории плазмы принято разделение на «близкие» и «далекие» пролеты при кулоновских взаимодействиях. Близкие пролеты дают рассеяние на большие углы, далекие - на малые. Условной границей между близкими и далекими пролетами выбрано значение прицельного параметра r_min = 2 r_^ . Интеграл в формуле (4.2.5) может быть в связи с этим разбит на две части:

(3.2.9)

Поскольку сила, действующая на кулоновский центр, находящийся в потоке частиц, пропорциональна кулоновскому логарифму, то разделение его на две части делит на две составляющие и эту силу. При этом вклад далеких пролетов оказывается определяющим :

3.2.2. Сила трения при кулоновском рассеянии частиц.

Определим теперь среднюю силу, действующую на заряженную частицу с массой m _a, зарядом e _a , движущуюся со скоростью u через среду, состоящую из частиц с массой m_b и зарядом e_b , распределенных по скоростям в соответствии с некоторой функцией распределения

По-прежнему считаем соударения парными. Выпишем уравнения движения для пары взаимодействующих частиц :

(3.2.10)

Удобнее перейти к рассмотрению движения центра инерции нашей механической системы, состоящей из двух частиц и относительного движения этих частиц. Введем радиус-вектор центра инерции :

(3.2.11)

и вектор относительного расстояния между взаимодействующими частицами :

(3.2.12)

Тогда радиус-векторы положения частиц можно выразить через эти новые переменные :

; (3.2.13)

и, подставив в (3.2.10) , получим уравнение движения центра инерции :

(3.2.14)

и уравнение относительного движения частиц :

(3.2.15)

где

Из (3.2.14) следует : , что соответствует состоянию равномерного прямолинейного движения или покоя (без ограничения общности рассмотрения можем положить ). Уравнение (3.2.15) напоминает любое из исходных уравнений движения частиц (3.2.10) и описывает движение некоторой частицы с массой m_ab в поле неподвижного кулоновского центра, что дает нам возможность использовать результат предыдущего параграфа.

Напомним, что нас интересует сила, действующая на пробную частицу a. Вернемся поэтому к выражению для ее радиус-вектора (первое из выражений (3.2.13). Умножим его на массу m _a и дважды продифференцируем по времени :

(3.2.16)

С учетом уравнения (3.2.14) это превратится в следующее соотношение :

(3.2.17)

означающее, что сила, действующая на частицу в единичном столкновении совпадает с силой как бы действующей на фиктивную частицу с приведенной массой, налетающей на воображаемый неподвижный центр. Этот неподвижный центр, как уже отмечалось в предыдущем параграфе, подвергается действию противоположно направленной силы той же величины.

Теперь мы должны построить промежуточную модель плоского потока рассеиваемых частиц. Выделим из всех частиц среды только частицы, имеющие скорость u^’ . Плотность частиц такого элементарного потока:

(3.2.18)

Заметим еще, что фиктивные частицы с «приведенной» массой налетают на воображаемый неподвижный рассеивающий центр со скоростью :

(3.2.19)

Теперь нам остается лишь заменить переменные в выражении (3.2.6) предыдущего параграфа в соответствии со следующей схемой :

; ; (3.2.20)

чтобы получить силу, действующую со стороны выделенного элементарного потока частиц на неподвижный центр :

(3.2.21)

Изменив знак силы на противоположный и интегрируя по всем скоростям, получаем:

(3.2.22)

причем в данном случае в кулоновский логарифм входит некая усредненная величина < r_^> :

(3.2.23)

где

Анализ выражения (3.2.22) дает, в частности, такой очень важный результат: сила трения при кулоновском рассеянии обратно пропорциональна квадрату модуля скорости

3.2.3.Передача энергии и импульса при кулоновских столкновениях.

Рассеяние быстрых частиц на бесконечно тяжелых полевых частицах. Простейшее время релаксации.

Удобной для дальнейшего использования величиной является так называемое простейшее время релаксации, введенное Б.А. Трубниковым (см. Сб. Вопросы теории плазмы т.1), равное характерному времени потери продольного импульса (рассеяния) быстрой частицы, движущейся в среде из бесконечно тяжелых полевых частиц. Мы можем получить его, используя выражение (3.2.22). Считаем, что а , где

- дельта функция Дирака. Записав уравнение движения рассеиваемой частицы для этого случая

и сравнивая его с записью уравнения для потери продольной скорости в - приближении

,

легко получаем выражение для

(3.2.24)

имея в виду, что .

Плоский поток в равновесной плазме

Пусть через однородную квазинейтральную плазму движется поток частиц a. Равновесная плазма состоит из ионов массы M и электронов массы m с максвелловским распределением всех частиц по скоростям. Температуры их равны: T_e=T_i=T. Нас интересуют три основных процесса:

— передача импульса частицами потока;

— рассеяние частиц;

— обмен энергией с плазмой;

Подсчитать передачу импульса от частицы a плазме мы можем используя

результаты, полученные в предыдущем параграфе. Для этого в уравнение движения этой пробной частицы подставляем силу трения из выражения (3.2.22) с учетом того, что в ее создании участвуют и ионы, и электроны плазмы

. (3.2.25)

Далее, в качестве функций распределения обоих сортов частиц, используем максвелловское распределение

считая его сферически симметричным.

Действуя по той же схеме, по которой мы получили простейшее время релаксации, записываем уравнение -приближения для потери продольного импульса частицами потока на плазме

и получаем характерное время продольного замедления частиц на частицах в равновесной плазме

(3.2.26)

Аналогично могут быть получены характерные времена поперечного рассеяния и потери энергии.

Полные времена релаксации: , , связаны с «частичными»: , , соотношениями вида:

Эти последние выражаются следующими формулами:

; ; (3.2.27)

В этих формулах использованы следующие обозначения:

; ; (3.2.28)

— интеграл Максвелла: . Приближенные выражения для в двух предельных случаях:

при (3.2.29)

при (3.2.30)

Нас интересуют столкновения типов: e/i ; e/e ; i/i ; i/e ;

Будем вначале считать, что энергия частиц потока очень велика, так, что всегда справедливо неравенство . Тогда: ; ; ;

Если теперь принять за единицу простейшее время релаксации электронов на ионах , получим следующие соотношения, объединенные в таблицу:

Условие применимости

Из анализа данных таблицы видно, что поток электронов большой энергии тормозиться на электронах всего вдвое быстрее, чем на ионах:

Поток ионов тормозится, в основном, на электронах:

Замедление и рассеяние электронов идет практически одновременно:

Ионы же замедляются, почти не рассеиваясь:

В случае, когда энергия частиц потока равна средней тепловой энергии частиц плазмы: , подобная таблица выглядит следующим образом:

Видно, что все релаксационные времена делятся на три группы: ; ; ;