Основы квантово-механической теории строения атома

В основе квантово-механической теории строения атома лежит планетарная модель Э. Резерфорда[1] (1911 г.), согласно которой атом состоит из положительно заряженного ядра и вращающихся вокруг него электронов (электронной оболочки). Поскольку объекты микромира не подчиняются законам классической механики и принципиально не возможно определить траекторию движения электрона, в квантовой механике понятие орбиты заменено понятием "орбиталь". Электронная орбиталь - это область околоядерного пространства, вероятность нахождения электрона в котором существенно отличается от нуля.

Важнейшими характеристиками орбитали являются граничная поверхность и функция радиального распределения вероятности нахождения электрона. Граничная поверхность орбитали определяет ее форму. Обычно граничная поверхность выбирается таким образом, чтобы она ограничивала околоядерное пространство с вероятностью нахождения электрона, равной 90%. Функция радиального распределения показывает вероятность нахождения электрона на разных удалениях от ядра. Для электронной орбитали основного состояния атома водорода граничная поверхность и функция радиального распределения вероятности имеют следующий вид.

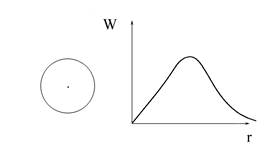
В квантовой механике каждой орбитали ставится в соответствие так называемая волновая функция (Y-функция, пси-функция). Сама по себе волновая функция не имеет физического смысла, но квадрат ее значения в какой-либо точке околоядерного пространства пропорционален вероятности нахождения электрона в бесконечно малом объеме, включающем эту точку (dV).

Волновые функции являются решениями волнового уравнения (Э. Шредингер[2], 1926 г.) - основного уравнения квантовой механики:

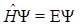(1)

где: Ĥ- оператор полной энергии (оператор Гамильтона, гамильтониан), Е - полная энергия системы.

Кажущаяся простота уравнения исчезает при раскрытии гамильтониана, который включает кинетическую часть и потенциальную энергию электрона (U):

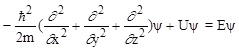(2)

Решение уравнения Шредингера связано с колоссальными сложностями. Строго оно может быть решено только для одноэлектронных систем, например, для атома водорода. В то же время, решение уравнения Шредингера даже для столь простых систем привело к двум интересным следствиям:

1. Решения волнового уравнения имеют дискретный характер и представляют собой набор волновых функций и соответствующих им квантованных значений энергии атома.

2. Волновые функции включают целочисленные параметры, изменяющиеся на единицу - квантовые числа. Поэтому орбитали атомы водорода можно качественно описать с помощью набора квантовых чисел. Каждое квантовое число играет важную роль, обеспечивая квантование (дискретность) определенной физической величины.

§ Главное квантовое число (n) - определяет энергию орбитали и среднюю удаленность электрона от ядра. Принимает значения 1,2,3,4 ... ¥. Соответственно этому электронная оболочка атома разбивается на ряд энергетических уровней (K,L,M,N...), расположенных на разных удалениях от ядра. Минимальную энергию имеет первый уровень. Энергия состояния, соответствующего ионизации атома (удаление электрона на бесконечное расстояние от ядра, n = ¥) принята за ноль.

§ Орбитальное квантовое число (l) - пробегает ряд значений от 0 до n-1 (при фиксированном n) и определяет орбитальный момент количества движения электрона, а фактически форму орбитали. Для многоэлектронных атомов l влияет также на энергию орбитали. Вследствие этого каждый энергетический уровень включает ряд подуровней с разными значениями орбитального квантового числа и орбиталями разной формы (s, p, d, f...).

§ Магнитное орбитальное квантовое число (m_l) - пробегает ряд значений от - l до + l и квантует проекцию орбитального момента электрона на одну из осей, определяя число орбиталей для каждого подуровня.

s-Подуровень содержит только одну орбиталь (l = 0, m_l = 0) сферической формы. р-Подуровень представлен тремя гантелевидными орбиталями, ориентированными по осям прямоугольной системы координат (p_x, p_y, p_z). (рис. 3.1).

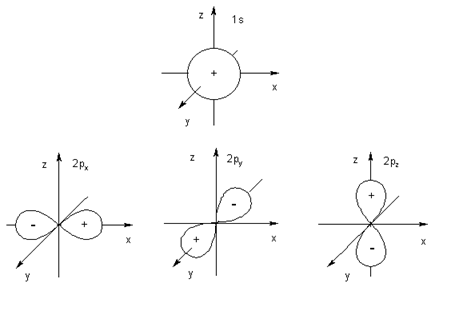
Рис. 3.1. Форма граничной поверхности s- и p-орбиталей. Указаны также математические знаки соответствующих волновых функций

Рассмотренные квантовые числа квантуют физические характеристики электронных орбиталей как областей пространства, в которых разрешено находиться электронам. Естественно, что, заняв ту или иную орбиталь, электрон автоматически принимает ее квантовые числа. Кроме этого, электрон имеет два собственных квантовых числа - спиновое и магнитное спиновое.

§ Спиновое квантовое число (s) квантует собственный вращательный момент количества движения элементарной частицы. Для электрона s = 1/2. Магнитное спиновое квантовое число (m_s) определяет проекцию собственного вращательного момента движения элементарной частицы на одну из осей и пробегает ряд значений от -s до +s. Для электрона магнитное спиновое квантовое число имеет два значения: -1/2 (b-спин) и +1/2 (a-спин).

Как уже отмечалось, строгое решение уравнения Шредингера возможно только для одноэлектронных атомных частиц. По этой причине для описания электронных оболочек многоэлектронных атомов приходится прибегать к ряду упрощений и приближений.

1.Принцип водородоподобного атома. Согласно этому принципу, электронную оболочку многоэлектронного атома можно описать набором орбиталей и квантовых чисел, аналогичным рассчитанным для атома водорода.

2.Принцип минимальной энергии - электроны заполняют орбитали в порядке увеличения их энергии. Последовательность увеличения энергии электронных орбиталей регламентируется правилами Клечковского[3]:

ü энергия орбиталей возрастает в порядке увеличения суммы главного и орбитального квантовых чисел (n+l);

ü при равных значениях (n+l) энергия орбиталей увеличивается с увеличением главного квантового числа.

В соответствии с правилами Клечковского энергия орбиталей будет увеличиваться в следующем ряду:

1s<2s<2p<3s<3p<4s<3d<4p<5s<4d<5p<6s<4f<5d...

3.Принцип запрета Паули[4] - невозможно существование двух электронов с одинаковым набором квантовых чисел. Отсюда следует, что электроны, расположенные на одной орбитали, могут различаться только значением спинового квантового числа, поскольку n, l и m_l являются характеристикой орбитали и автоматически передаются ее электронам, а спиновое квантовое число электрона фиксировано (s = 1/2). Поскольку спиновое магнитное квантовое число электрона принимает два значения, на одной орбитали могут одновременно находиться только два электрона с разной ориентацией спина. Наличие у электрона спина и его ориентация передается в электронных формулах стрелкой: a-спин (m_s = +1/2) - ­; b-спин (m_s = -1/2) - ¯. Во внешнем магнитном поле состояние с b-спином имеет меньшую энергию. В отсутствие магнитного поля энергия состояний с a- и b-спином одинакова.

4.Правило Гунда[5] - при заполнении энергетического подуровня электроны стремятся занять максимальное число орбиталей, ориентируя спин параллельно. Например, при реализации конфигурации p³ электроны заполняют орбитали следующим образом:

.

Исходя из рассмотренных принципов, рассмотрим строение электронных оболочек атомов элементов малых периодов периодической системы. Именно эти периоды представляют наибольший интерес для химиков-органиков, поскольку включают основные элементы-органогены (H, C, N, O, P, S).

Первый периодпредставлен двумя элементами - водородом и гелием, у которых заполняется первый энергетический уровень.

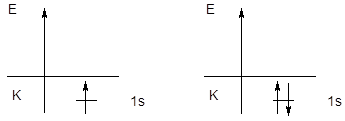
H: 1s¹ He: 1s²

При составлении электронной формулы атома или другой атомной частицы числом указывается главное квантовое число, буквой - орбитальное квантовое число и верхним индексом - число электронов на подуровне.

Поскольку емкость первого уровня ограничена двумя электронами, следующий элемент - литий начинаетвторой период, у элементов которого происходит последовательное заполнение второго энергетического уровня, начиная с конфигурации 1s²2s¹ (Li) и заканчивая конфигурацией 1s²2s²2p⁶ (Ne).

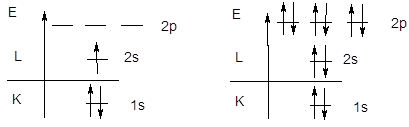
Li: 1s²2s¹ ........ Ne: 1s²2s²2p⁶

Аналогичным образом происходит заполнение s и p-подуровней третьего энергетического уровня у элементов третьего периода (начиная с натрия и заканчивая аргоном): Na: KL3s¹; Ar: KL3s²3p⁶.

Далее следовало бы ожидать заполнения орбиталей 3d-подуровня. Однако у элементов четвертого периода начинается заполнение четвертого уровня, поскольку энергия 4s-подуровня ниже, чем энергия 3d-орбиталей – K: KLM4s¹; Ca: KLM4s². После заполнения 4s-орбитали, в соответствии правилами Клечковского, начинается заполнение 3d-подуровня. Поскольку d-подуровень вмещает 10 электронов, этот процесс охватывает 10 элементов (от скандия до цинка).

3.2. ОСНОВЫ КВАНТОВО-МЕХАНИЧЕСКОЙ ТЕОРИИ ХИМИЧЕСКОЙ СВЯЗИ

Ø Химическая связь - это результат электростатического взаимодействия ядер и электронов, приводящего к образованию устойчивой совокупности атомов - молекулярных частиц или атомных агрегатов.

Движущей силой образования химической связи является стремление системы к минимуму энергии при достижении завершенной электронной оболочки инертного газа (s² или s²p⁶). В зависимости от способа приближения системы атомных частиц к устойчивому состоянию различают три типа химической связи: ковалентную, ионную и металлическую. В теории химической связи обычно рассматривают также силы межмолекулярного взаимодействия (силы Ван-дер-Ваальса[6]), являющиеся по своей сути физическим взаимодействием, и водородную связь, лежащую на границе физического и химического взаимодействия.

С развитием квантово-механических представлений в теории химической связи сложились два метода описания ковалентной связи: метод валентных связей (метод ВС) и метод молекулярных орбиталей (метод МО).

Согласно методу ВС атомы, составляющие молекулу, сохраняют свою индивидуальность, а химические связи возникают в результате взаимодействия их валентных электронов и валентных орбиталей. Метод МО рассматривает молекулу как единое образование, в котором каждый электрон принадлежит частице в целом и движется в поле всех ее ядер и электронов. Методы ВС и МО, несмотря на существенные различия в подходах к описанию молекул, хорошо дополняют друг друга. Во многих случаях они приводят в конечном итоге к одинаковым результатам.

3.2.1. Основные положения методавалентных связей

Ковалентная связь реализуется за счет образования общей электронной пары при перекрывании электронных орбиталей взаимодействующих атомов. Выделяют два механизма образования общей электронной пары - обменный и донорно-акцепторный.

§ При реализации обменного механизма каждый из взаимодействующих атомов предоставляет на образование общей электронной пары неспаренный электрон, занимающий валентную орбиталь. По данному механизму образованы связи в молекуле метана.

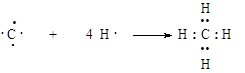
§ При образовании ковалентной связи по донорно-акцепторному механизму один из атомов выступает в качестве донора, предоставляя в общее пользование неподеленную пару электронов, расположенную на одной из его валентных орбиталей. Второй атом - акцептор - предоставляет на образование связи вакантную орбиталь, принимая на нее электронную пару партнера-донора. По донорно-акцепторному механизму образуется связь N-H при протонировании аммиака и аминов.

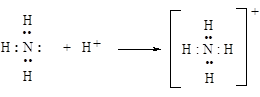
· По числу общих электронных пар, связывающих атомы, различают простые, двойные и тройные связи.

H₃С:СH₃ или H₃C-CH₃

H₂C::CH₂ или H₂C=CH₂

HC:::CH или HCºCH

· По характеру перекрывания взаимодействующих орбиталей в органической химии выделяют два типа ковалентной связи: s-связь,при образовании которой перекрывание орбиталей происходит вдоль линии связи (линии, соединяющей ядра взаимодействующих атомов); p-связь,при образовании которой перекрывание орбиталей происходит в плоскости, содержащей линию связи (боковое перекрывание).

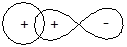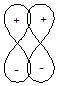v Характеристики связи. Важнейшими физическими характеристиками химической связи являются ее энергия и длина.

ØЭнергия химической связи – это количество энергии, необходимое для ее разрыва.

Такое же количество энергии выделяется при образовании связи. Так, энергия диссоциации молекулы водорода составляет 435 кДж/моль. Соответственно, E_H-H = 435 кДж/моль.

ØДлина связи – расстояние между ядрами химически связанных атомов.

Она измеряется в нм (нанометр, 1×10^-9 м) или пм (пикометр, 1×10^-12 м). Энергии и длины основных связей в молекулах органических соединений приведены в табл. 3.1.

Таблица 3.1