Уравнение состояния идеального газа
1.1. Резиновый мяч объемом V0 = 1 л наполнен воздухом при атмосферном давлении p0 = 105 Па. Масса мяча m=200 г. Мяч погружают в воду, и, начиная с некоторой глубины h, он уже не может самостоятельно всплыть. Полагая температуру воздуха в мяче неизменной, вычислить эту глубину.
1.2.Поршневой насос качает воздух в баллон объемом V, захватывая из атмосферы за каждый цикл объём воздуха DV. Начальное давление в баллоне – атмосферное p0. Считая процесс изотермическим, вычислить давление pN в баллоне после N циклов качаний.
1.3.В баллоне объемом V = 1 л находится азот массой m=0,28 г. Азот нагрели до температуры Т=1500 °С, при которой 30% всех его молекул диссоциированы на атомы. Вычислить давление р в баллоне.
Первый закон термодинамики
2.1.Взяв V1=2 л одноатомного газа при р1=105 Па и Т1 = 300 К, нагрели его до Т2 = 320 К, уменьшив его объем до V2=1 л. Процесс провели так, что на диаграмме (р, V) он изображается прямой линией. Определить работу газа и изменение его внутренней энергии.
2.2. Моль гелия нагревают от температуры T1 до T2. Процесс проводят так. что давление гелия пропорционально его объему. Определить работу гелия и его теплоемкость в этом процессе.
2.3. Найти молярную теплоёмкость С одноатомного газа в процессе, при котором Т=αр2 (α – постоянная).
Циклические процессы
2.1. С молем идеального газа проводится циклический процесс, состоящий из двух изобар и двух изохор (рис. 2.1). Известны температуры T1 и T3, а также то, что точки 2 и 4 лежат на одной изотерме. Определить работу газа за цикл.
2.2. С некоторым газом (не обязательно идеальным) провели два процесса: 0-1 и 0-2, показанных на рис. 2.2, причем конечные состояния 1 и 2 лежат на одной адиабате. В каком процессе к газу подвели больше тепла? Ответ обосновать.
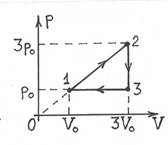
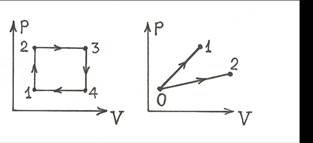
Рис. 2.1 Рис. 2.2 Рис. 2.3
2.3. Определить КПД цикла, показанного на рис. 2.3, если рабочим телом является одноатомный идеальный газ.
7. ЗАДАЧИ СЕМИНАРОВ
1. Кинематика точки
1.1. (1.1). Первую половину суток паровоз шел со скоростью υ1=60 км/ч, а вторую половину – со скоростью υ2=90 км/ч. Вычислить среднюю скорость паровоза за сутки.
Ответ. <υ>=(υ1+υ2)/2=75 км/ч.
1.2. (1.2). Первую половину пути паровоз прошел со скоростью υ1=60 км/ч, а вторую половину – со скоростью υ2=90 км/ч. Вычислить среднюю скорость паровоза на всём пути.
Ответ. <υ>=2υ1υ2/(υ1+υ2)=72 км/ч.
1.3. (1.3). Ежедневно от А до Б и обратно летает вертолёт без посадки в Б. Скорость вертолёта относительно воздуха υ=108 км/ч. Вчера было тихо, а сегодня вдоль курса подул ветер со скоростью u=20 м/с. Во сколько раз изменится время полёта?
 Ответ. Увеличилось в υ2/(υ2−u2)=1,8 раза.
Ответ. Увеличилось в υ2/(υ2−u2)=1,8 раза.
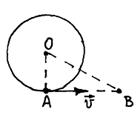
1.4. (1.21*). В некоторый момент времени скорость объекта А, находящегося на вращающейся карусели, с точки зрения неподвижного наблюдателя В равна υ. Каковы величина и направление скорости υ′ объекта В с точки зрения наблюдателя А, если ОА=R, OB=2R?
 Ответ. υ′=2υ, υ′
Ответ. υ′=2υ, υ′ 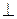 ОВ.
ОВ.
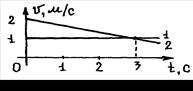
1.5. (1.28). Две частицы начинают движение вдоль оси х из точки х=0. Графики υ(t) частиц показаны на рисунке. Определить время и точку, где частицы встретятся вновь. Построить графики х(t).
Ответ. t=6 с, х=6 м.
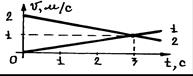 1.6. (1.29). Две частицы начинают движение вдоль оси х из точки х=0. Графики υ(t) частиц показаны на рисунке. Определить время и точку, где частицы встретятся вновь. Построить графики х(t).
1.6. (1.29). Две частицы начинают движение вдоль оси х из точки х=0. Графики υ(t) частиц показаны на рисунке. Определить время и точку, где частицы встретятся вновь. Построить графики х(t).
Ответ. t=6 с, x=6 м.
1.7. (1.30). Тело начинает двигаться из состояния покоя с постоянным ускорением. В первую секунду оно проходит путь 1 м. Сколько метров оно пройдет за вторую секунду?
Ответ. 3м.
1.8. (1.36). Поезд, двигаясь под уклон, прошел путь 340 м за 20 с и достиг скорости υ2= 19 м/с. Найти скорость υ1 поезда в начале уклона.
Ответ. 15 м/с.
1.9. (1.37). Тело движется равноускоренно с начальной скоростью υ0=1 м/с. Пройдя некоторый путь, оно приобрело скорость υ1=7 м/с. Вычислить скорость тела на середине этого пути. Ответ. 5 м/с.
1.10. (1.50). Камень бросили вертикально вверх со скоростью υ0=20 м/с. Через какое время он будет находиться на высоте h=15 м и какую он при этом будет иметь скорость? Изобразить график движения камня у(t).
Ответ. t=1 с, 3 с; υ=10 м/с..
1.11. (1.51).Камень, брошенный вертикально вверх, находился на высоте 15 м два раза с интервалом 2 с. Определить начальную скорость камня.
Ответ. υ0=20 м/с.
1.12. (1.61).Камень бросили с земли с начальной скоростью υ0 под углом α к горизонту. Определить: 1) время полета t; 2) дальность полета s; 3) высоту полета h; 4) уравнение траектории у(х).
Ответ. 1) 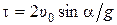 ; 2)
; 2) 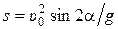 ; 3)
; 3) 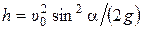 ;
;
4) 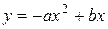 , где
, где 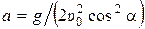 , b=tg a.
, b=tg a.
1.13. (1.64). Шарик бросают горизонтально. Во сколько раз увеличится дальность полета, если вдвое увеличить: а) начальную скорость; б) высоту, с которой бросают шарик ?
Ответ. а) в 2 раза; б) в 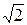 раза.
раза.
1.14. (1.65). Двое играют в мяч, бросая, его друг другу. Какой наибольшей высоты достигает мяч, если от одного игрока до другого он летит 2 с?
Ответ. 5 м.
1.15. (1.66).При каком угле бросания дальность полета камня равна высоте его подъёма?
Ответ. tg a = 4, a = 76°.
1.16. (1.71). Снаряд вылетает из пушки со скоростью υ0=600 м/с. Под каким углом a надо выставить ствол, чтобы снаряд упал на расстоянии s=18 км от пушки? Каково время его полета?
Ответ. a1=15°, a2=75°. t1=31 с, t2=116 c.
Уравнения движения
2.1. 1.86. Поезд трогается. Вагоны разгоняет сила тяги со стороны паровоза. А какая внешняя сила разгоняет паровоз?
2.2. 1.87. Двое перетягивают канат. Второй оказался сильнее Первого и перетягивает его. Значит ли это, что Второй тянет канат с большей силой?
2.3. 1.88.Длина тормозного следа машины на асфальте s=20 м. С какой скоростью ехала машина, если коэффициент трения её колёс k=1,0?
Ответ. 72 км/ч.
2.4. 1.89.При скорости υ1=40 км/ч тормозной путь автомобиля s1=4 м. Каков будет тормозной путь s2 при скорости υ2 = 60 км/ч, если коэффициент трения остается тем же?
Ответ. 9 м.
2.5. 1.91. Шайба пересекла ледяное поле длиной 50 м за 5 с и остановилась. Определить начальную скорость шайбы и её коэффициент трения о лед, считая его постоянным на всем пути.
Ответ. 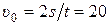 м/с;
м/с; 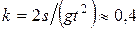 .
.
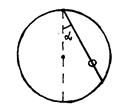 2.6. 1.96.По хорде окружности под углом
2.6. 1.96.По хорде окружности под углом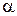 к вертикали натянута нить, по которой без трения может скользить бусинка (см. рис.). Определить время соскальзывания бусинки по нити, если радиус окружности равен R, а бусинка начинает движение сверху (задача Галилея).
к вертикали натянута нить, по которой без трения может скользить бусинка (см. рис.). Определить время соскальзывания бусинки по нити, если радиус окружности равен R, а бусинка начинает движение сверху (задача Галилея).
Ответ. 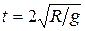 и не зависит от угла a..
и не зависит от угла a..
2.7. 1.102*. Кубик начинает скользить без трения с вершины наклонной плоскости, длина основания которой l=2,1 м. При каком угле наклона a время соскальзывания будет минимальным? Каково это время?
Ответ. a=45°, t=0,92 с.
2.8. 1.110. Машина проезжает вогнутый участок дороги радиусом R=40 м со скоростью υ=72 км/ч. Во сколько раз давление машины на дорогу будет больше веса машины? Принять g=10 м/с2.
Ответ. В 2 раза.
2.9. 1.111. С какой максимальной скоростью может ехать автомобиль по горизонтальной дороге, описывая дугу радиусом R=100 м, если коэффициент трения резины о дорогу k=0,4?
 Ответ. 20 м/с.
Ответ. 20 м/с.
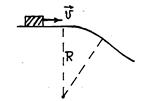
2.10. 1.112. Горизонтальный участок дороги плавно, дугой радиусомR, переходит в спуск (см. рис.). Автомобиль начинает отрываться от дороги в самом начале такого спуска при минимальной скорости υ = 72 км/ч. Определить радиус дуги на спуске.
 Ответ. 40 м.
Ответ. 40 м.
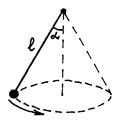
2.11. 1.114. Маленький шарик вращается на нити по окружности, как показано на рисунке (конический маятник). Определить период его движения, если длина нити l=1 м, а угол ее отклонения a=60°.
Ответ. 1,4 с.
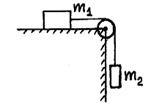 2.12. 1.128. Через блок на краю стола перекинута нить, а к ней привязаны грузы
2.12. 1.128. Через блок на краю стола перекинута нить, а к ней привязаны грузы 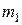 =3 кг и
=3 кг и 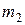 =1 кг (см. рис.) Коэффициент трения груза
=1 кг (см. рис.) Коэффициент трения груза 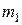 о стол
о стол 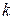 =0,2. Вычислить ускорение системы и натяжение нити.
=0,2. Вычислить ускорение системы и натяжение нити.
Ответ. а = 1 м/с, Fн=9 Н.
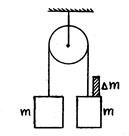 2.13. 1.136. На нити, перекинутой через блок, висят два одинаковых груза массами
2.13. 1.136. На нити, перекинутой через блок, висят два одинаковых груза массами 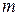 . На правый кладут довесок массой
. На правый кладут довесок массой 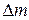 (см. рис.). Определить ускорение системы и силу давления довеска на правый груз.
(см. рис.). Определить ускорение системы и силу давления довеска на правый груз.
Ответ. 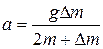 ,
, 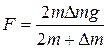 .
.
