Порядок выполнения работы. Закрыв плотно экран В, открывают кран Е и накачивают в сосуд (или выкачивают) воздух

Закрыв плотно экран В, открывают кран Е и накачивают в сосуд (или выкачивают) воздух. Закрывают кран Е, ожидают, когда установится постоянное давление воздуха в сосуде. После этого производят отчет разности Η₁ уровеня жидкости в коленах манометра. Затем открывают на короткое время кран В, соединяют воздух сосуда с атмосферным воздухом и в момент, когда давление в сосуде будет равно атмосферному, закрывают кран. Снова ожидают, когда установится давление в сосуде после прошедшего адиабатного расширения (или сжатия).

Производят отчет по манометру величины Η₂ и вычисляют значение величины γ по формуле (7).

Опыт повторяют не менее пяти раз и из всех значений величины определяют среднее значение 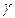. Все результаты измерений записывают в таблицу. Рекомендуемая форма протокола выполнения лабораторной работы приведены ниже.

Протокол лабораторной работы №7

№ опытов		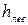	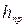Η1		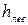	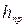Η2	γ	Δγ

Среднее значения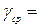

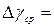
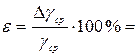
Результат: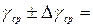

Вопросы для самопроверки к работе №7

1. Напишите уравнение I начала термодинамики.

2. Что такое внутренняя энергия газа?

3. Что такое молярная теплоемкость при и .

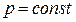4. Напишите уравнение Майера.

5. Запишите I начало термодинамики для изохорического, изобарического и изотермического процессов.

6. Какой процесс называется адиабатным?

Запишите соотношение между P и V, T и V при адиабатном процессе.

Список рекомендуемой литературы

1. Дмитриева В.Ф., Прокофьев В.Л. Основы физики. – М.: Высшая школа, 2009.

2. Трофимова Т.И. Курс физики. – М.: Высшая школа, 2010.

Материально–техническое обеспечение

1. Установка для лабораторной работы по молекулярной физике «Определение показателя степени в уравнении Пуассона методом Клемана – Дезорма».

2. Программа для моделирования лабораторной работы на компьютере.

Лабораторная работа №8.

«Определение коэффициента вязкости жидкости по методу Стокса»

Краткая теория.

Движение молекул газа в термодинамической равновесной системе полностью хаотично. Из основных представлений кинетической теории следует, что газы испытывают в 1 секунду порядка 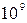столкновений (соударений). Число столкновений (среднее) за 1с

,

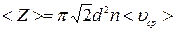где d – эффективный диаметр молекул газа;

n – концентрация (т.е. число молекул в единице объёма); ;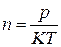

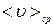– средняя арифметическая скорость молекул.

Расстояние, которое проходит молекула между двумя последовательными соударениями называется средней длиной свободного пробега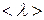

;

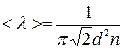В газах и жидкостях вследствие хаотичного движения молекул происходит необратимый процесс переноса различных физических величин. Эти явления объединяются общим названием «явление переноса».

I. Перенос массы от мест с более высокой концентрацией молекул к местам с более низкой концентрацией называют диффузией.

Эта масса определяется уравнением:

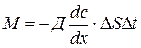
Здесь 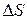– площадка, нормальная к потоку продиффундирующему через неё массы М;

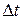– время движения молекул через площадку ;

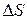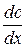– градиент концентрации; 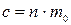; 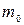– масса одной молекулы газа;

Д – коэффициент диффузии: .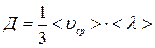

II. Перенос импульса молекулами из соприкасающихся слоёв газа или жидкости, в которых молекулы движутся с разными скоростями в одном направлении, определяют силы внутреннего трения (их называют вязкостью).

Сила внутреннего трения F между двумя слоями жидкости определяется уравнением

,

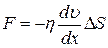здесь 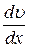– градиент скорости, т.е. изменение скорости на единицу длины в направлении оси х.

Коэффициент вязкости 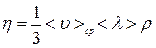, где 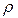– плотность газа или жидкости.

III. Перенос энергии происходит вследствие хаотичного движения молекул из областей с более высокой температуры и обладающих большей энергией ( 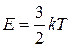) в области с более низкой температурой. Этот процесс называется теплопроводностью. Перенос энергии определяется уравнением

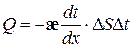
где Q – количество теплоты, перенесённое через изотермическую площадку 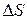за время ;

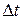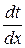– градиент температуры;

х – коэффициент теплопроводности.

;

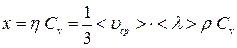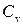– удельная изохорическая теплоёмкость.

При движении тела в вязкой среде возникает сопротивление этому движению. При малых скоростях и обтекаемой форме тела сопротивления обусловлена вязкостью жидкости. Слой жидкости, непосредственно прилегающий к твёрдому телу, прилипает к его поверхности и увлекается им. Следующий слой увлекается за телом с меньшей скоростью. Таким образом, между слоями возникают силы внутреннего трения.

При падении шарика радиуса r в вязкой жидкости, находящеёся в мензурке (рис. 1), на него действует две противоположно направленные силы. Одна из них f обусловлена гравитацией за вычетом выталкивающих (архимедовой) силы. Другая сила F обусловлена внутренним тернием. Из теории следует, что

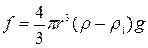(1)

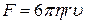(2)

где 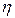– коэффициент вязкости (или внутреннего трения);

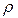– плотность вещества шарика;

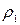– плотности жидкости;

g – ускорение силы тяжести;

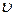– скорость шарика.

Цель работы – измерение вязкости жидкости 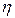методом Стокса.

Как видно из (2), сила растёт с увеличением скорости до тех пор, пока не установится равенство сил f и F:

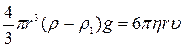(3)

С этого момента шарик движется равномерно и прямолинейно (установившиеся движение). Из (3) следует, что коэффициент вязкости

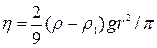(4)

В методе Стокса по этой формуле, измерив r и 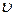и пользуясь известными значениями 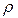, 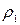и g, определяют вязкость жидкости.