Критерии плазменного состояния

Итак, критериями плазменного состояния вещества являются следующие неравенства:

d << L ; N_D 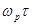>>>1 ; > 1

1.5. Температура плазмы

Из курса общей физики известно, что молекулы (атомы) газа, находящегося в

состоянии теплового равновесия, распределены по скоростям в соответствии с законом Максвелла:

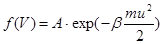(1.5.1)

Температура обычно вводится как величина, обратно пропорциональная параметру b , определяющему ширину распределения, а коэффициентом пропорциональности является постоянная Больцмана:

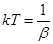(1.5.2)

При этом температура измеряется в градусах Кельвина.

В физике плазмы за коэффициент пропорциональности обычно выбирают единицу; тогда температура измеряется в энергетических единицах. Удобная величина – электронвольт:

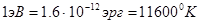
Физический смысл понятия температуры можно уточнить, если выразить среднюю энергию частицы в системе, имеющей максвелловсое распределение. Эта связь, как известно из общей физики, выглядит следующим образом:

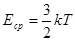, если T измеряется в градусах Кельвина и

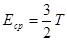, если T измеряется в энергетических единицах.

Отсюда ясно, почему температура часто отождествляется со средней энергией частиц в тепловом движении.

Если все компоненты плазмы имеют одинаковую температуру, то говорят о полном термодинамическом равновесии. В случае, если температуры различных компонент отличаются друг от друга, равновесие называется частичным. Так довольно часто встречается ситуация, при которой ионы и электроны плазмы имеют различные температуры из-за различных скоростей установления равновесия внутри каждой из компонент и между компонентами.

1.6. Тепловая и кулоновская энергия.

Плотность тепловой энергии для равновесной плазмы выражается так же, как и для

идеального газа:

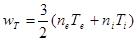(1.6.1)

n_e, n_i – число частиц в единице объема для электронной и ионной компонент, соответственно; T_e и T_i - температуры компонент (в энергетических единицах).

Кроме тепловой энергии в плазме в отличие от идеального газа существует еще энергия кулоновского (электростатического) взаимодействия, однако, поскольку потенциал частицы действует в первом приближении только внутри дебаевской сферы, плотность электростатической энергии можно считать пренебрежимо малой по сравнению с плотностью тепловой энергии. Оценки дают величину

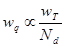(1.6.2)

где N_d – число частиц в дебаевской сфере. При N_d >>1, что и требуется для признания ионизованного газа плазмой, плазма, с точки зрения термодинамики, может быть рассматриваема, как идеальный газ.

1.7. Равновесие ионизации и формула Саха.

При рассмотрении состояния, промежуточного между нейтральным газом и

полностью ионизованной плазмой, говорят обычно о степени ионизации газа или плазмы. В рамках термодинамического подхода речь идет о равновесной степени ионизации. Равновесие же в полном смысле этого слова существует в замкнутых системах, каковыми практически никогда не являются экспериментальные и технологические плазменные установки. Через них обычно проходят потоки частиц и энергии. Эти потоки могут быть стационарными и в таких открытых системах могут устанавливаться стационарные состояния, не совпадающие, вообще говоря, с состоянием термодинамического равновесия.

Имея в виду эту оговорку, рассмотрим систему, в которой идет процесс ионизации газа и обратный ему процесс рекомбинации. Пусть, например, ионизация осуществляется электронным ударом, а рекомбинация тройным столкновением:

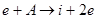
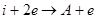
Соответствующие скорости реакций могут быть записаны как:

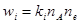(1.7.1.)

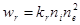(1.7.2)

Здесь 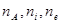- соответствующие концентрации. Константы скоростей реакций 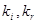зависят только от температуры. В соответствии с принципом детального равновесия, в равновесном состоянии скорости прямого и обратного процессов должны быть равны.

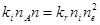(1.7.3)

Из (2.3.3) прямо следует:

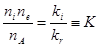(1.7.4)

Величина K называется константой равновесия, а само соотношение (2.3.4) – законом действующих масс. Аналогичные рассмотрения можно провести и для других пар прямых и обратных процессов; вне зависимости от конкретного механизма результат будет одинаков и выразится в общем виде таким образом:

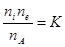(1.7.4а)

Частный случай выражения (1.7.4а) для идеальной равновесной плазмы называется формулой Саха по имени индийского астрофизика, который ее получил. Формула Саха справедлива, если плазму можно рассматривать как идеальный газ, если работает принцип детального равновесия и если плазма идеальна: число частиц в дебаевской сфере должно быть велико. Ниже приводится один из возможных выводов формулы Саха.

Итак, пусть система равновесна и вероятность для частицы находиться в

состоянии с энергией E дается формулой Больцмана:

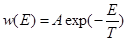(1.7.5)

Полное число частиц с энергией E равно вероятности для частицы находиться в

состоянии с энергией E, умноженной на число таких состояний (статистический вес) . Если частица не имеет внутренних степеней свободы, то число состояний равно числу элементарных ячеек фазового пространства объемом h³ , где h – постоянная Планка. Для электрона с импульсом между p и p+dp фазовый объем:

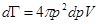(1.7.6)

где U - объем обычного пространства. Число электронов в этом элементе фазового объема:

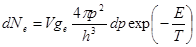(1.7.7)

g_e – статистический вес, то-есть число состояний с одинаковой энергией. В случае электронов считаем энергию электрона в атоме за нулевой уровень. Тогда для свободного электрона с импульсом p выражение для энергии будет выглядеть так:

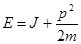(1.7.8)

J – потенциал ионизации атома. Число свободных электронов на один атом в данном квантовом состоянии получится при интегрировании по всем возможным значениям импульса:

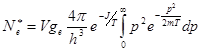(1.7.9)

Интегрирование дает:

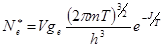(1.7.9)

При интегрировании использована формула:

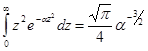, полагая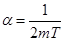

Полное число электронов получится, если результат (1.7.9) умножить на число атомов в одном квантовом состоянии 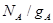, где g_A – полный статистический вес нейтрального атома:

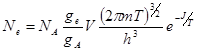(1.7.10)

Чтобы учесть вклад ионов в равновесие, нужно принять за объем U объем, приходящийся на один ион в определенном квантовом состоянии:

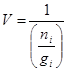(1.7.11)

где n_i – концентрация ионов, g_i – статистический вес иона. Подставив (1.7.11) в (1.7.10), получаем окончательно:

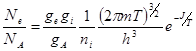(1.7.12)

И, поскольку отношение полных чисел частиц равно отношению концентраций, (1.7.12) можно переписать в виде, подобном (1.7.4а):

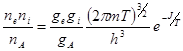(1.7.13)

Справа здесь стоит величина, названная выше константой равновесия. Если подставить цифры соответствующих констант и иметь температуру в электрон-вольтах, то (1.7.13) будет выглядеть так:

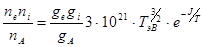(1.7.13а)

Размерность концентраций здесь см^-3.

Глава 2. Способы описания плазмы.

2.1. Одночастичное приближение

Первым логическим шагом в изучении плазмы – системы, поведение

которой определяется движением множества заряженных частиц, является рассмотрение поведения отдельной заряженной частицы во внешних полях.

2.1.1. Простейший случай: B = const.; E = 0.

Пусть магнитное поле направлено вдоль оси z: B = Be_z (e_z – единичный вектор в направлении оси z). Движение частицы, имеющей массу m и заряд q , будет при этом описываться системой уравнений

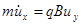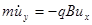
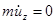, , , (2.1.1)

где u_x , u_y и u_z – компоненты скорости по соответствующей координате, а точка над величиной соответствует производной по времени.

Продифференцировав уравнения системы (2.1.1) еще раз по времени и произведя соответствующие подстановки, получим

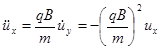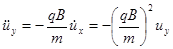, . (2.1.2)

Эти уравнения являются уравнениями гармонического осциллятора, работающего на частоте

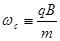(2.1.3)

называемой обычно циклотронной частотой.

Интегрируя уравнения (3.1.2), получаем

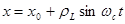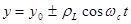; ; (2.1.4)

вращение по круговой орбите радиусом

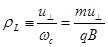(2.1.5)

вокруг ведущего центра с координатами (x_0, y₀ ). На произвольное движение вдоль оси z магнитное поле не влияет.

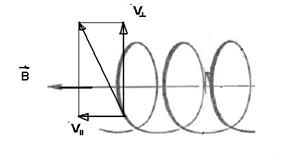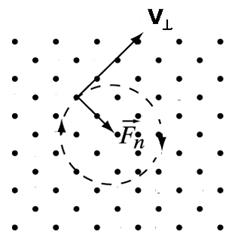Рис. 2.1. Движение заряженной частицы в однородном магнитном поле

2.1.2. Случай: B = const.; E = Const.

Добавим теперь электрическое поле E = Const. Пусть магнитное поле по-прежнему направлено вдоль оси z (или направление оси z выбрано вдоль магнитного поля). У поля E всегда можно выделить две компоненты – продольную (вдоль B) и поперечную (^B). Движение заряженной частицы вдоль магнитного поля может рассматриваться независимо, а поперечную компоненту электрического поля мы можем (для определенности и без нарушения общности) направить вдоль оси x.

Движение вдоль оси z – это движение с постоянным ускорением, вызываемым силой q E. В данном параграфе оно не будет нас интересовать. Мы можем также вывести из рассмотрения быстрое ларморовсое вращение частицы вокруг ведущего центра, усреднив уравнение движения

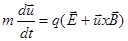(2.1.6)

по отрезку времени, много большему чем период ларморовского вращения. При этом получим

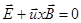(2.1.7)

Умножая векторно на B имеем 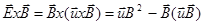, или, выделив поперечные компоненты:

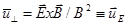(2.1.8)

Здесь 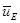- скорость движения ведущего центра при наличии электрического поля (или скорость дрейфа частицы в электрическом поле). Видно, что она не зависит ни от каких параметров заряженной частицы, а зависит только от внешних полей. Это означает, в частности, что ионы и электроны дрейфуют в одном и том же направлении и с одинаковой скоростью.

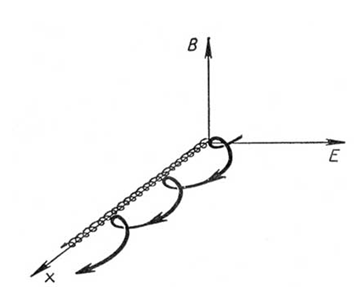Рис.2.2. Дрейф электронов и ионов в скрещенных полях

2.1.3. Обобщение понятия дрейф частицы.

Обратим внимание на возможность замены в уравнении (3.1.6) силы q 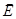, действующей на заряженную частицу со стороны электрического поля, любой другой внешней силой. такая возможность приводит к возможности обобщения понятия дрейф частицы.

Нетрудно видеть, что для скорости дрейфа получается следующее общее выражение:

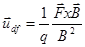(2.1.9)

Рассмотрим некоторые из интересных частных случаев.