Волновые методы исследования плазмы

4.5.1. Измерение плотности плазмы по отсечке СВЧ излучения

Полное отражение электромагнитной волны от плазмы при равенстве частоты этой волны плазменной частоте используется для определения плотности плазмы. Применяемая при этом схема измерения приведена на рисунке 4.5.1.

Рисунок 4.5.1. Схема измерения плотности плазмы по отсечке СВЧ излучения.

Определяется частота, при которой интенсивность проходящего на приемник сигнала обращается в нуль. Значение плотности вычисляется из условия отсечки

.

При этом

.

Существенным недостатком описанной схемы является то, что отсечка происходит, если плотность плазмы превышает критическую даже локально в любом месте на пути волнового луча. Плазма может быть сосредоточена, к примеру, в малой центральной области и практически отсутствовать во всем объеме установки.

4.5.2. СВЧ интерферометрия

Гораздо более информативна методика СВЧ интерферометра. Плотность плазмы измеряется при этом по сдвигу фазы электромагнитной волны при ее прохождении сквозь плазму. Схема измерения видоизменяется (см. рисунок 4.5.2). Часть сигнала, выходящего из генератора, ответвляется в так называемый опорный канал, в котором установлены аттенюфтор и фазовращатель, позволяющие регулировать амплитуду и фазу волны в опорном сигнале. Опорный сигнал затем складывается с сигналом, прошедшим через плазму по основному измерительному каналу. Регулировка опорного сигнала производится так, чтобы в отсутствие плазмы сигнал на регистраторе был равен нулю, т.е. чтобы происходило взаимное погашение волн (Фазы сдвинуты на 180⁰). При появлении плазмы в измерительном канале, фаза проходящей по нему волны сдвигается и измеритель регистрирует появление сигнала.

Фазовый сдвиг, возникающий при прохождении электромагнитной волны сквозь плазму, легко рассчитывается из следующих соображений. Сдвиг фазы измерительной и опорной волн определяется различием фазовых скоростей в опорном плече (вакуумная скорость, с) и в измерительном плече (скорость распространения волны в плазме ). При одинаковом геометрическом расстоянии l времена прохождения точки с одинаковой фазой опорного и измерительного плеча

и ,

Разность их и определит фазовый сдвиг :

(4.5.2.1)

Рисунок 4.5.2. Схема СВЧ интерферометра.

Показатель преломления электромагнитной волны, распространяющейся в холодной плазме дается выражением: , с помощью которого получаем

,

или, считая, что <<1, и используя разложение по малому параметру

, получаем . (4.5.2.2)

Используя выражение для плазменной частоты : и имея в виду, что частота, на которой производится измерения, определяет критическое значение плотности плазмы, получим окончательно

(4.5.2.3)

Глава 5. Объемный заряд в плазме

5.1. Задача о плоском диоде

Начнем с рассмотрения модели, которую можно представить как предельный

случай пристеночного слоя плазмы. Рассмотрим плоский диод – систему, состоящую из двух бесконечных пластин 1 и 2, расположенных параллельно одна другой на расстоянии d. Одна из пластин является эмиттером заряженных частиц, ускоряемых по направлению ко второй разностью потенциалов U =  - _1. Без ограничения общности можем считать потенциал эмиттера нулевым (₁ = 0). Пусть ось x направлена перпендикулярно пластинам, плотность тока частиц, эмиттируемых с нулевыми начальными скоростями пластиной 1 равна j , масса каждой частицы m , а ее заряд q . Будем искать распределение потенциала между пластинами вдоль оси x .

Воспользуемся уравнением Пуассона, которое в данном случае будет одномерным

(5.1)

где (x) en(x)- распределение плотности заряда вдоль оси x . С учетом сохранения плотности тока вдоль x : j = en(x) u(x) = const. (u – скорость частиц вдоль оси, зависящая от пройденной разности потенциалов и, следовательно, от координаты) выразим (x):

(5.2)

и, подставив в (5.1), получим

(5.3)

Обозначив: , перепишем уравнение (5.1.3) в виде:

(5.3а)

Первый интеграл уравнения (5.3а) получим, умножив обе его части на ,

после чего оно превратится в:

(5.4)

Откуда следует:

(5.5)

В случае постоянная интегрирования С также обращается в нуль, следовательно имеем:

(5.6)

Интегрируем затем (5.6), преобразовав его

после чего получим:

(5.7)

где при принятых условиях: U=0 при x=0, постоянная интегрирования также приравнивается нулю. Таким образом имеем окончательный ответ:

(5.1.8)

Подставляя теперь в (5.8) значение B, перепишем его:

(5.9)

Имея в виду, что при принятых условиях, потенциал второго электрода равен разности потенциалов между пластинами ( ), выразим, используя (6.1.9), плотность тока, проходящего через диод с расстоянием d между электродами при разности потенциалов U между ними:

(5.10)

Выражение (5.10) называется законом Чайлда-Ленгмюра или законом «3/2».

Если U выражено в Вольтах, j – в Амперах и d – сантиметрах, то «Закон 3/2» будет выглядеть следующим образом :

M – масса частиц в единицах протонной массы. В частности для электронов M=1/1840 и выражение примет вид

5.2. Плоский слой

Перейдем теперь к исследованию стационарной ситуации при которой поток холодных ионов (T_i= 0) плазмы идет на стенку вдоль оси x, ускоряясь полем слоя (которое одновременно препятствует уходу электронов). Будем считать, что в точке x = 0 скорость ионов u_{i =} u₀ и плотность n₀ .

Используем, как и в предыдущем случае, одномерное уравнение Пуассона. Здесь нам придется учесть уже два сорта частиц, вносящих вклад в формирование плотности объемного заряда: ионы и электроны. Плотность ионов можно выразить с помощью следующих соображений : они ускоряются электростатическим полем при сохранении плотности потока .

Запишем для потока ионов закон сохранения энергии :

(5.11)

и уравнение непрерывности:

(5.12)

Выразив затем из (6.11) текущую скорость ионов U(x) , получим с помощью (6.12) текущую плотность ионов:

(5.13)

Что касается электронов, то для них примем Больцмановское распределение:

(5.14)

Тогда уравнение Пуассона запишется в следующем виде:

(5.15)

Уравнение (5.15) можно переписать более компактно:

, (5.16)

если ввести безразмерные переменные:

; ; ; . (5.17)

Первое интегрирование уравнения (5.17) можно провести в общем виде, домножив обе его части на :

(5.18)

Учитывая, что при , (поле в плазме отсутствует), получаем:

(5.19)

Дальнейшее интегрирование может быть выполнено только численно, однако и не производя его можно получить важный результат, проанализировав полученное уравнение (5.19). Видно, что его правая часть должна быть всегда положительна. Если рассмотреть область малых ( ), то, разложив ее в ряд по степеням и ограничиваясь членом второго порядка, получим условие существования решения уравнения(5.19):

(5.20)

Это неравенство называется критерием Бома, обуславливающим существование стационарного слоя в плазме. Для образования такого слоя необходимо, чтобы ионы, подходящие из плазмы к его границе, имели скорость, превышающую скорость ионного звука. Чтобы ионы в плазме могли набрать такую скорость, необходимо допустить существование электрического поля в области, предшествующей слою. Таким образом условие (5.20), полученное в предположении нуля поля и потенциала на границе слоя, строго говоря противоречат этим предположениям, которые могут быть теперь приняты только в качестве приблизительных. Можно предлагать различные формальные оправдания приемлемости проведенного рассмотрения от неопределенности положения границы слоя с плазмой до не вполне больцмановского распределения электронов. Физика же дела состоит в следующем: в слое плотность ионов всюду должна спадать медленнее, чем плотность электронов. При этом весь избыток положительного заряда окажется сосредоточенным вблизи стенки.

Если перейти теперь в область больших ( ), то плотностью электронов можно пренебречь и уравнение (6.16) будет выглядеть следующим образом:

, (5.21)

что с точностью до обозначений совпадает с использованным в предыдущем параграфе уравнением (5.3а), решение которого дает закон Чайлда-Ленгмюра для униполярного потока частиц в плоском диоде.

Проведенное рассмотрение дает возможность качественно описать распределение потенциала вблизи стенки состоящим из трех областей: предслоя – области в плазме с плавным нарастанием потенциала, где ионы набирают скорость, необходимую для формирования слоя – области, в которой происходит отражение основной массы электронов; размер этой области – несколько дебаевских радиусов и, наконец, области диода, размер которой определяется законом 3/2 при плотности потока ионов, определяемой скоростью рождения их в плазме. Разность потенциалов на этом диоде определяется необходимостью поддержания равенства потоков ионов и электронов на стенку.

5.. Плоский зонд

Полученный критерий можно использовать для оценки величины ионного тока насыщения, приходящего на плоский зонд, помещенный в плазму. Площадь собирающей поверхности зонда примем равной ; на зонд подан большой отрицательный потенциал, полностью препятствующий попаданию на него плазменных электронов и собирающий все приходящие на поверхность ионы. Как следует из полученного критерия, эти ионы имеют направленную скорость

(5.22)

Тогда ионный ток на зонд определится формулой:

(5.23)

где n_гр – плотность плазмы у внешней границы слоя. Определим положение этой границы, как места, где скорость ионного потока в точности равна скорости ионного звука. Для достижения такой скорости ионы должны пройти разность потенциалов , следовательно, граница слоя имеет по отношению к плазме отрицательный потенциал такой величины. Принимая электроны распределенными по Больцману, оценим их плотность в этом месте:

(5.24)

Полагая плазму квазинейтральной, перепишем соотношение (6.1.23) с учетом (6.1.24):

(5.25)

С помощью этой формулы, измеряя ионный ток на зонд и зная температуру плазмы, можно оценить ее плотность:

(5.26)

Погрешности результатов вычислений по формуле (5.26) помимо неопределенности положения границы слоя обычно связаны с неопределенностью величины собирающей поверхности зонда.

5.4 Расходимость пучка заряженных частиц.

Рассмотрим плоский (ленточный) пучок заряженных частиц с зарядом q, массой m и энергией движущихся в направлении z. Будем считать, что плотность потока однородна по сечению и, что в плоскости z = 0 скорости всех частиц направлены вдоль оси z . Его размер в направлении y считаем много большим, чем в направлении x.

Рис. 5.3. Форма огибающих расходящегося пучка. Заштрихованные прямоугольники – распределение плотности тока по сечению. a₀ - начальная полутолщина пучка, d₀ – полуширина (считаем ее неизменной).

Собственный объемный заряд пучка вызывает поперечное расталкивание составляющих его частиц. Уравнение Пуассона для рассматриваемого случая имеет вид

(5.27)

где , - плотность тока в плоскости z = 0. а – текущая полутолщина пучка,

- продольная скорость частиц пучка.

Откуда получаем величину напряженности электрического поля на границе пучка:

(5.28)

и записываем уравнение движения для крайней частицы, движущейся по огибающей:

(5.29)

Интегрируя (5.29) с учетом следующих начальных условий: a(0) = a₀ , , и принимая во внимание, что (т.е. z = u_zt), получаем уравнение огибающей пучка:

(5.30)

или

поскольку , где - разность потенциалов, пройденная частицами пучка при их ускорении, то последнее выражение можно привести к виду

(5.31)

где - предельная плотность тока эффективного диода, в котором мог быть ускорен рассматриваемый пучок, а l - ширина этого диода.

Приложения

Приложение 1. Использованная и рекомендуемая литература

1. Д.А. Франк-Каменецкий, Лекции по физике плазмы,

Атомиздат , Москва 1968.

2. В.М. Кулыгин, «Начала физики плазмы», Москва, изд. МЭИ, 2001, (имеется в электронном виде)

3. В.М.Белокопытов, В.М. Кулыгин, «Элементы теории термоядерной плазмы», М: Изд. МЭИ, 2005, 84 стр.

4. Ф. Чен, Введение в физику плазмы, «Мир» , Москва, 1987.

5. К.Миямото, Основы физики плазмы и управляемого синтеза, Москва, 2007, Физматлит

6. В.Е. Голант, А.П. Жилинский, С.А. Сахаров, Атомиздат, Москва, 1977.

7. Сб. Вопросы теории плазмы, т.1, Госатомиздат, Москва, 1963.

8. А.Б. Михайловский, Теория плазменных неустойчивостей, т.1, Атомиздат, Москва, 1970.

9. Б.Б. Кадомцев, Коллективные явления в плазме, Наука, Москва, 1988.

10. А.А. Веденов, Задачник по физике плазмы, Атомиздат, Москва, 1981.

11. В.И. Ильгисонис и др. Сборник задач по физической электронике и физике плазмы, Москва, МИФИ, 2008.

Приложение 2. Задачи

Глава 1

1.1.Вычислить величины дебаевского радиуса и плазменной частоты для следующих случаев :

А) плазма токамака ( n = 10¹⁴ см^-3 , Т_е = 40 КэВ );

Б) разряд в ионном источнике ( n = 10¹² см^-3 , Т_е = 8 эВ );

В) ионосфера Земли ( n = 10⁶ см^-3 , Т_е = 0.1 эВ ).

1.2.Вычислить число частиц в дебаевской сфере для тех же случаев.

1.3.Вычислить давление плазмы в термоядерном реакторе ( n = 5. 10¹⁴ см^-3 , Т_е = 30 КэВ ).

1.4.Температура плазмы в установке Токамак равна 20кэВ. Скольким

градусам Кельвина это соответствует?

1.4.Вычислить плотность тепловой энергии плазмы в термоядерной

установке, если ее плотность см^-3, а температура кэВ.

1.5.Оценить плотность кулоновской энергии для термоядерной плазмы по параметрам предыдущей задачи.

1.6.Вычислить степень ионизации для малой примеси и для основной

компоненты плазмы, если константа равновесия ионизации задана.

Решение:

Степень ионизации . Концентрация электронов определяется основной компонентой плазмы, поэтому для примеси ее можно считать заданной. Тогда, имея в виду заданную константу равновесия ионизации.

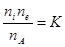, получаем . ( ; )

Для основной компоненты концентрация электронов определяется равновесием ионизации. При однократной ионизации . Тогда из соотношения равновесия следует . Если степень ионизации велика, то следует исходить из заданности начальной концентрации атомов . Тогда или . Взяв положительный корень этого квадратного уравнения, получаем выражение для степени ионизации:

Если степень ионизации мала, то и , откуда .

1.7. Найти температурную зависимость равновесной концентрации электронов для слабоионизованной плазмы, имеющей потенциал ионизации основной компоненты J.

Решение:

Из результата предыдущей задачи следует, что для слабоионизованной плазмы . По формуле Саха видно, что константа равновесия зависит от температуры следующим образом

При малой степени ионизации можно пренебречь статистическими весами возбужденных состояний и учитывать только статвеса основных состояний (которые от температуры не зависят). При этом

1.8.Найти зависимость степени ионизации от концентрации для стационарного (но не равновесного) состояния в плазме, из которой излучение выходит свободно, так, что ионизация производится электронным ударом, а рекомбинация – с излучением. Ионизацией под действием излучения можно пренебречь из-за прозрачности плазмы, тройной рекомбинацией – из-за малой плотности.

Решение:

Приравнивая скорости ионизации электронами и рекомбинации парными столкновениями с излучением: , имеем:

. Величина здесь уже не может быть найдена из термодинамики. Она определится сечениями процессов ионизации и рекомбинации. Стационарное состояние ионизации не зависит от концентрации электронов. Степень ионизации выразится соотношением:

, в которое не входит концентрация электронов. Это не зависит от того, является ли вещество малой примесью или это основная компонента плазмы.

Глава 2

2.1.Вычислить ларморовский радиус

А) дейтона с энергией 15 КэВ, движущегося в однородноммагнитном поле 0.85 Т под углом 60⁰ к силовым линиям;

Б) электрона с энергией 10 КэВ движущегося в однородном магнитном поле 0.6 Т под углом 45⁰ к силовым линиям;

В) ядра атома гелия с энергией 3 МэВ движущегося в однородном магнитном поле 0.7 Т под углом 45⁰ к силовым линиям.

2.2. Вычислить значения циклотронных частот для тех же случаев.

2.3.Вычислить скорость дрейфа электрона в скрещенных электрическом ( E = 100 В/см) и

магнитном H = 0.1 T ) полях.

2.4.Рассмотреть движение заряженной частицы в поле прямого тока.

2.5.Выразить в явном виде условие применимости дрейфового приближения для движения заряженной частицы в магнитном поле прямого тока.

2.6.Плазменный цилиндр находится в скрещенных полях: продольном

магнитном и радиальном электрическом. Найти энергию системы, считая, что вращение плазмы происходит со скоростью электрического дрейфа.

2.7.Сравнивая энергию системы по задаче 2.6. с энергией цилиндрического конденсатора, определить эффективную диэлектрическую проницаемость плазмы.

2.8.Плазма, цилиндрической формы, имеет диаметр D и находится во внешнем продольном магнитном поле. Сформулировать количественно условие ее замагниченности.

Решение:

Чтобы частицы плазмы не уходили сразу на стенку установки, их ларморовский радиус должен быть существенно меньше характерного поперечногоразмера системы (в данном случае – диаметра установки. Таким образом имеем условие:

,

кторое, после подстановки выражения для ларморовского радиуса, запишется (с точностью до множителя, порядка единицы):

Где - отношение газокинетического давления плазмы (плотность тепловой энергии) к магнитному; - погонное число частиц , R₀= - так называемый классический радиус частицы, определяемый из условия равенства кулоновской энергии частицы и ее собственной энергии .

2.9.Как изменится уравнение диффузии магнитного поля в плазму, если учесть токи смещения?

Решение:

Выпишем нужное нам уравнение Максвелла с учетом тока смещения: , выразим из него и подставим в (2.2.27). Получим:

. Взяв ротор от обеих частей равенства, и учитывая, что , получим уточненное уравнение диффузии магнитного поля:

вместо прежнего

2.10. Плазма, находящаяся в зеркальной ловушке с пробочным отношением R_m = 4, имеет изотропное распределение частиц по скоростям. Столкновения отсутствуют, так что частицы, попавшие в конус потерь, сразу уходят, а не попавшие – остаются. Определить долю захваченных частиц.

Указание:

Покидают систему частицы, у которых в центральной части ловушки питч-угол орбиты меньше значения, определяемого соотношением:

. В интересующем нас случае R_m=4, следовательно, в ловушке останутся частицы с питч-углами, синус которых превышает

Глава 3

3.1. В установке получен высокий вакуум при давлении остаточного газа (азот) Тор. Перевести это значение в Па. Вычислить длину свободного пробега молекул газа.

3.2.Пучок электронов с энергией 80 эВ проходит через молекулярный

водород. Определить число протонов, рождающихся в секунду в 1 см³ .

3.3.Водород, десорбируемый со стенки плазменной установки в виде

молекул, летит в плазму со следующими параметрами см^-3 , эВ. Определить глубину проникновения его в плазму в виде нейтрального газа.

3.4.Решить предыдущую задачу для параметров термоядерной плазмы по

задаче 2.2.

3.5.Вычислить значение кулоновского логарифма для газоразрядной плазмы

плотностью см^-3 при температуре электронов эВ.

3.6.Пучок электронов с энергией 40 эВ влетает в газоразрядную водородную

плазму с параметрами, данными в предыдущей задаче. Определить характерное время его торможения за счет кулоновских столкновений.

3.7.Пучок быстрых атомов водорода, инжектированный тангенциально в

плазму токамака, захватывается в ней в виде быстрых ионов, движущихся вдоль оси установки. Оценить количество оборотов, которое ионы пучка совершат до потери своей энергии (до уровня температуры плазмы), если энергия инжекции равна 1МэВ, а параметры плазмы: см^-3 , кэВ, при большом радиусе токамака R= 5.5 м.

Глава 4

4.1.Для определения плотности плазмы используется СВЧ интерферометр с длиной волны 6 мм. До какого значения плотности эти измерения могут производиться.

4.2.Вывести дисперсионное соотношение для высокочастотных электромагнитных волн, распространяющихся в холодной плазме без магнитного поля. Столкновениями пренебречь.

4.3.Связь с космическим кораблем поддерживается с помощью передатчика, работающего на частоте 450 МГц. Достаточна ли высока частота для прохождения ионосферы ? Какова критическая плотность плазмы, вызывающая прерывание связи ?

4.4.Каково должно быть соотношение между циклотронными частотами и плазменной частотой чтобы альфвеновская скорость была много меньше скорости света?

4.5.Вычислить групповую скорость прямых магнитозвуковых волн в плотной плазме.

4.6.Выразить фазовую скорость волн на электронной плазменной частоте в

функции плотности и температуры плазмы.

4.8. Выразить фазовую скорость магнитозвуковой волны как функцию частоты в плотной горячей плазме.

Глава 5

5.1.Плотность ионного тока насыщения, приходящего на плоский зонд 10

мА\см² . Вычислить плотность плазмы, если температура электронов равна 5 эВ.

5.2.Источник пучка ионов водорода (протия) , используемый в инжекторе

быстрых атомов токамака Т-15, формирует пучок с энергией 40 КэВ. Считая, что ионно-оптическая система (ИОС) источника может быть представлена как эффективный плоский диод, оценить плотность тока, при которой он работает . Учесть при этом, что напряжение между электродами ИОС ограничено условием пробоя U[KВ] = 80 ( l [см] )^1/2 .

5.3. Критерий существования стабильного слоя выведен для случая плазмы с холодными ионами. Как изменится пороговая величина средней скорости ионного потока при наличии теплового размытия ионных скоростей?

Ответ:

Пороговая скорость должна быть больше значения, полученного для холодных ионов. Важна величина объемного заряда, создаваемого ионной компонентой, а, следовательно – пролетной плотности ионов. Ионы, имеющие скорости большие средней, дают меньший вклад в пролетную плотность, чем относительно медленные ионы. Разброс в сторону меньших скоростей сильнее увеличивает пролетную плотность, чем уменьшает ее разброс в сторону больших скоростей. Это должно быть скомпенсировано большей средней скоростью.