Краткое теоретическое введение

Согласно квантовой теории излучение света атомами веще­ства связано с изменением их энергетического состояния. Атом, излучающий квант света (фотон) частотой v, уменьшает свою энергию на величину 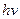. Величина 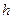называется постоянной Планка и является одной из мировых универсальных констант. По теории Бора переход атома водорода из одного энергетиче­ского состояния в другое связан с переходом электрона атома с одной орбиты на другую. Орбиты электрона в атоме квантованы, и поэтому энергия атома водорода не может иметь любое произ­вольное значение. Дозволенные значения энергии 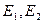... в со­вокупности образуют линейчатый энергетический спектр. По теории Бора дозволенные значения энергии атома водорода рас­считывают по формуле (1), в которую входят: 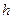- постоянная Планка; 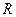- постоянная Ридберга; 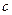- скорость распространения света в вакууме; 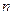- номер энергетического состояния атома (но­мер уровня).

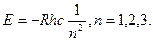(1)

Число 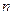одновременно указывает номер орбиты, отсчиты­ваемой от ядра, на которой находится электрон в данном энерге­тическом состоянии атома. При 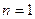атом водорода обладает наименьшей энергией (электрон при этом находится на орбите, ближайшей к ядру). Такое состояние атома называется нормаль­ным. Состояния, для которых 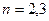..., являются возбужденными. Атом водорода, находясь в этих состоя­ниях, обладает большими значениями энер­гий. Энергетический спектр атома водорода, рассчитанный по формуле (1), и переходы, соответствующие линиям серии Бальмера. При переходе электрона с более удаленной орбиты на более низкую излучается квант света частотой 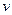, уносящий с собой энергию

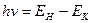. (2)

В формуле (2) 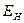и 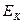представляют энергии атома в на­чальном и последующих состояниях. Эти энергии можно вычис­лить из (1), если известны числа 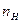и .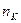

В спектре атома водорода одна из групп спектральных ли­ний соответствует переходам электрона на вторую орбиту ( 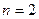) с более удаленных от ядра высоких орбит ( 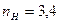...). Эти ли­нии образуют серию Бальмера и имеют частоты, соответствую­щие видимой области оптического спектра. Частоты и длины волн в спектре излучения атома водорода можно рассчитать, ис­пользуя формулы (1) и (2). Для линий серии Бальмера

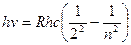, где 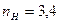... (3)

Вместо (3) можно записать (4), если учесть, что :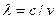

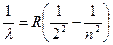. (4)

По теории Бора постоянная

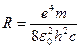, (5)

где 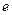- заряд электрона, 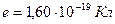; 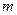- масса покоя элек­трона, 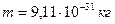; 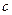- скорость света в вакууме, 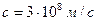; 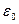- электрическая постоянная, .

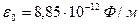Из (4) и (5) находим :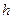

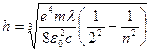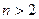при (6)

Это соотношение удобнее привести к виду (7), обозначив постоянный множитель через 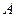, который можно вычислить зара­нее

;

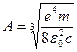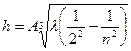. (7)

Формула (7) показывает, что для определения постоянной Планка нужно измерить длины волн спектра излучения атомов водорода, соответствующих переходам электрона: с уровня 3 на уровень 2 (красная линия спектра); с уровня 4 на уровень 2 (голубовато-зеленая линия); с уровня 5 на уровень 2 (фиолетовая линия).

Методика определения постоянной Ридберга и Планка

Постоянная Ридберга рассчитывается по формуле (5), по­стоянная Планка - по формуле (7). Для определения постоянной Планка необходимо измерить длины волн спектра атома водоро­да в серии Бальмера (красной линии, голубовато-зеленой линии и фиолетовой линии).

Чтобы измерить длины волн спектральных линий неиз­вестного спектра с помощью гониометра, необходимо, прежде всего, знать постоянную дифракционной решетки, используемой в данной работе. Для этого надо измерить углы дифракции, под которыми будут наблюдаться спектральные линии известного спектра, например спектра излучения ртутной лампы. Постоян­ная решетки находится из условия усиления света при дифрак­ции

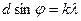, (8)

где 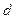- постоянная решетки; 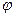- угол дифракции; 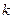- порядок спектра; 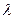- длина волны монохроматического света. Зная постоянную решетки и заменив ртутную лампу на водородную, определяют углы дифракции, под которыми наблюдаются линии водородного спектра, а затем, пользуясь формулой (8), определяют длины волн наблюдаемых линий в спектре излучения атомов водорода.

Задание

1. Ознакомьтесь с работой гониометра-спектрометра ГС-2.

2. Определите постоянную дифракционной решетки, исполь­зуемой в гониометре ГС-2 в качестве спектрального прибора.

3. Измерьте спектр излучения атома водорода.

4. Рассчитайте постоянную Планка и постоянную Ридберга.