Выполнение упражнений и обработка результатов измерений

1. Нарисовать таблицу 5.1.

2. Определить атмосферное давление .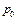

3. Определить температуру воздуха в лаборатории .

4. По справочным таблицам определить давление насыщенных паров воды при данной температуре 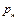и плотность воды .

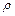5. Подать на установку питание, переведя тумблер в положение «ВКЛ». При этом загорается сигнальная лампа.

6. В модуле «ПОДСВЕТКА КАПИЛЛЯРА» перевести тумблер в положение «ВКЛ». При этом загорается сигнальная лампа.

7. Повернуть тубус микроскопа «на себя» и установить его в положение удобное для работы.

8. Отрегулировать подсветку капилляра соответствующим потенциометром.

9. При помощи регулировочного винта добиться четкого изображения края капилляра. Установить его на нулевое деление шкалы микроскопа и зафиксировать положение рабочего элемента винтом.

10. Сфокусировать микроскоп на мениске жидкости.

11. Определить положение мениска, т.е. расстояние 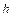от верхнего края трубки до поверхности воды (рис. 5.4).

12. Из-за испарения воды положение мениска будет меняться (обозначим новое положение мениска 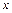). Через каждые 5 минут фиксировать положение мениска с помощью шкалы микроскопа. В таблицу 5.1 записать не менее 10 показаний положения мениска.

Таблица 5.1

№	х, мкм	t, c
…

13. Построить график зависимости положения края мениска 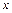от времени 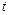: 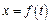. Она должна быть линейной.

14. По графику, как угловой коэффициент полученной прямой определить скорость испарения воды .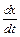

15. По формуле (5.9) определить коэффициент диффузии 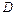паров воды в воздухе.

16. Оценить погрешность измерения. Сравнить полученный результат с табличным значением.

4. Контрольные вопросы

1. Что такое явления переноса? Какие явления переноса, изучаемые в термодинамике, Вы знаете? Охарактеризуйте их.

2. Выведите общее уравнение переноса. Что означает знак «минус» в этом уравнении?

3. Какой физический смысл имеет коэффициент диффузии? Как он зависит от температуры и давления?

4. Какой пар называется насыщенным? Как давление насыщенного пара зависит от температуры?

5. Что такое добавочное давление над вогнутой поверхностью? Чем оно определяется?

6. Что такое длина свободного пробега молекул? Как она зависит от температуры и давления газа?

7. Какие системы называются термодинамически неравновесными?

Лабораторная работа № 6

ОПРЕДЕЛЕНИЕ МОЛЯРНОЙ ТЕПЛОТЫ

ПАРООБРАЗОВАНИЯ ВОДЫ

Цель работы: определение молярной теплоты парообразования воды.

Приборы и материалы: экспериментальная установка ФПТ1-10, термометр, вакууметр, исследуемая жидкость (вода).

Краткая теория

Различают три агрегатные состояния вещества: твердое, жидкое и газообразное. Часто четвертым агрегатным состоянием вещества называют плазму. Также в термодинамике термодинамически равновесное состояние вещества, отличающееся по своим физическим свойствам от других возможных равновесных состояний того же вещества называют фазами. Например, лед, жидкая вода и пар – фазы воды. Однако, понятие фаз является более широким, чем понятие об агрегатных состояниях: могут существовать различные фазы и в пределах одного и того же агрегатного состояния. Так, область твердого состояния не является обычно вся одной и той же фазой. При различных давлениях и температурах вещество может находиться в различных кристаллических состояниях, каждое из которых характеризуется своей определенной структурой. Эти различные состояния тоже представляют собой различные фазы вещества, их называют кристаллическими модификациями, а о свойстве вещества обладать несколькими такими фазами говорят как о полиморфизме. Известными примерами являются модификации углерода (графит и алмаз), серы (образующие ромбические и моноклинные кристаллы), кремнезема (различные минералы – кварц, тридимит, кристобалит) и т.д. Говоря о твердом состоянии, как об особой фазе вещества (отличной от жидкой фазы), имеют в виду лишь твердое кристаллическое состояние. Аморфное твердое тело превращается при нагревании в жидкость путем постепенного размягчения, без всякого скачка, поэтому аморфное твердое состояние не представляет собой особой фазы вещества. Так, не являются различными фазами твердое и жидкое стекло.

Значение температуры, давления или какой-либо другой физической величины, при котором происходит фазовый переход, называют точкой перехода. Различают фазовые переходы двух родов. При фазовым переходе I рода скачком меняются такие термодинамические характеристики вещества, как плотность, концентрация компонентов, внутренняя энергия; в единице массы выде­ляется или поглощается вполне опре­деленное количество теплоты, называемое скрытой теплотой (или тепло­той фазового перехода).

Фазовые переходы I рода – широко распростра­ненное в природе явление. К ним от­носятся: плавление и затвердевание, испарение и конденсация, сублима­ция и конденсация в твердую фазу (десублимация), а также некоторые структурные переходы в твердых телах, например образование мартенсита в сплаве железо-углерод. В чистых сверхпро­водниках достаточно сильное магнитное поле вызывает фазовый переход I рода из сверх­проводящего в нормальное состояние.

Для фазовых переходов II рода характерно от­сутствие скачков плотности вещества, кон­центрации компонентов, нет изменения внутренней энергии. Теплота фазового пере­хода II рода равна нулю. К фазовым переходам II рода относятся: переход парамагнетик – ферромагнетик, со­провождаемый появлением макроскопического магнитного момента; переход парамаг­нетик – антиферромагнетик, сопро­вождаемый появлением антиферромагнитного упорядочения; переход параэлектрик – сегнетоэлектрик с появ­лением самопроизвольной (спонтан­ной) поляризации вещества; переход метал­лов и сплавов из нормального в сверхпрово­дящее состояние, переход ³Не и ⁴Не в сверхтекучее состояние и т.д.

Как уже отмечалось, переход I рода вещества из одной фазы в другую всегда связан с поглощением или выделением некоторого количества тепла (теплоты перехода). В случае перехода жидкости в газ говорят о теплоте парообразования, в случае перехода твердого тела в жидкость – о теплоте плавления.

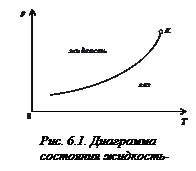
Переход из одной фазы в другую при заданном давлении происходит всегда при строго определенной температуре. И вообще, две любые фазы вещества могут находиться в тепловом равновесии лишь при определенном давлении, которое зависит от температуры. Эту зависимость можно изобразить графически на так называемой фазовой диаграмме (или диаграмме состояний), на осях которой откладывают давление 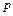и температуру 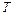. Например, на рис. 6.1 изображена кривая испарения (она же кривая конденсации).

Соотношение, связывающее давление и температуру при равновесии двух фаз можно записать в виде:

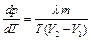, (6.1)

где 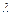– удельная теплота фазового перехода, 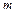– масса вещества, 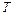– абсолютная температура фазового перехода, 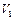и 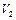– объемы вещества в первом и втором фазовых состояниях.

Соотношение (6.1) называют уравнением Клапейрона–Клаузиуса. Если в правой части равенства массу системы перенести в знаменатель и почленно поделить на нее объемы 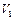и 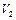, то получим:

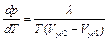, (6.2)

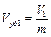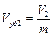где и – соответственно удельные объемы вещества в первом и во втором фазовых состояниях, т.е. до и после расширения в процессе фазового перехода.

Если при записи уравнения (6.2) теплоту 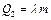определять через количества вещества 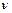, тогда 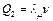, где 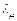– молярная теплота фазового перехода. В случае перехода системы из жидкого состояния в парообразное 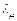– молярная теплота парообразования, т.е. количество теплоты, необходимое для испарения одного моля вещества. Таким образом:

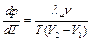. (6.3)

Если в правой части последнего равенства количество вещества 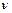перенести в знаменатель и почленно поделить на нее объемы 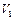и 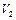, то получим:

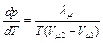, (6.4)

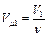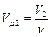где величины и – соответственно молярные объемы вещества в первом и во втором фазовых состояниях.

Пар, находящийся в термодинамическом равновесии со своей жидкостью называется насыщенным, а о его давлении говорят как о давлении насыщенного пара. Тогда кривую равновесия жидкость – пар можно рассматривать как кривую зависимости давления насыщенного пара от температуры.

Если известны как функции температуры и давления удельная или молярная теплота парообразования и удельные или молярные объемы, то уравнения (6.2) или соответственно (6.4) можно проинтегрировать и найти для насыщенного пара в явном виде зависимость давления от температуры. В самом грубом приближении можно считать, что 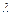или 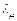не зависит от температуры, а удельным или молярным объемом жидкости по сравнению с удельным или молярным объемом для насыщенного пара можно пренебречь. При не очень высоких температурах плотность насыщенного пара не велика, и его можно рассматривать как идеальный газ и применять к нему уравнение Клапейрона–Менделеева.

Если рассматривать равновесное состояние жидкости и газа, то для него выражение (6.4) можно записать так:

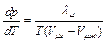(6.5)

Для одного моля вещества 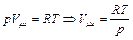, 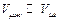. Учитывая это условие в (6.5), получим:

.

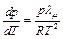Разделим переменные в полученном дифференциальном уравнении:

.

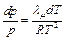Проинтегрируем это выражение:

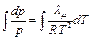, откуда:

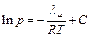, (6.6)

где С – константа, получаемая при нахождении неопределенного интеграла (она может быть выражена любым образом и обычно ее записывают в виде удобном для дальнейших преобразований). Если, например, ее представить как 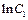, то окончательно получаем:

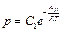. (6.7)

Согласно (6.7) давление насыщенного пара растет с температурой очень быстро – по экспоненциальному закону.

В обычных условиях над поверхностью жидкости, помимо ее собственного пара, находится смесь других газов – воздух. Это обстоятельство мало сказывается на самом фазовом равнове­сии: испарение продолжается до тех пор, пока парциальное дав­ление пара не сделается равным давлению насыщенного пара при температуре жидкости.

Наличие атмосферы, однако, существенно влияет на ход про­цесса испарения. Картина этого процесса выглядит совершенно различным образом в зависимости от того, будет ли давление на­сыщенного пара при данной температуре меньше или больше об­щего давления, под которым находится жидкость.

В первом случае происходит сравнительно медленное испаре­ние жидкости с ее поверхности. Правда, непосредственно над по­верхностью парциальное давление пара почти сразу делается равным давлению насыщенного пара. Но этот насыщенный пар медленно (путем диффузии) распространяется в окружаю­щее пространство, и только по мере его перемешивания с возду­хом испаряются новые порции жидкости. Естественно, что ис­кусственное сдувание пара с поверхности жидкости увеличивает скорость испарения.

Характер процесса меняется, когда давление насыщенного пара достигает (или начинает несколько превосходить) давление окружающей атмосферы – возникает кипение жидкости. Оно характеризуется бурным образованием по всему объему жидкости газовых пузырьков, растущих путем испарения жидкости внутрь этих пузырьков и затем поднимающихся через жидкость, перемешивая ее. При этом от свободной поверхности жидкости распространяется в окружающую атмосферу струя пара.

В данной работе применимы допущения, сделанные при выводе формулы (6.6), поэтому мы можем воспользоваться ею для определения молярной теплоты парообразования воды. Запишем уравнение (6.6) для двух различных состояний:

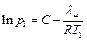, (6.8)

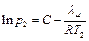. (6.9)

Вычтем (6.8) из (6.9). Получим:

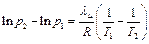. (6.10)

Из формулы (6.10) выразим :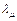

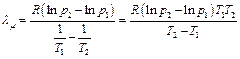. (6.11)

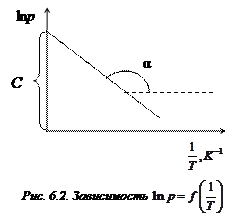Графически зависимость 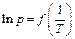выглядит так, как показано на рис. 6.2. Угловой коэффициент наклона этой прямой отрицателен. Учитывая этот минус в уравнении (6.9) и выражая из него 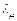, получим:

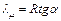. (6.10)