Краткие теоретические сведения

Внутренняя энергия телавключает в себя кинетическую энергию теплового движения молекул, потенциальную энергию взаимодействия между всеми молекулами и внутримолекулярную энергию всех молекул. Последняя состоит из кинетической энергии движения частей молекул друг относительно друга и потенциальной энергии их взаимодействия. Обозначается внутренняя энергия буквой U. Она является функцией состояния тела, это означает, что она зависит только от состояния и не зависит от способа, каким телом приведено к этому состоянию.

В соответствии с законами механики изменение внутренней энергии 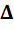Uравно работе всех сил, действующих на тело. Работа же разделяется на работу сил, действующих на тело в целом и вызывающих изменение его объема, (обозначается 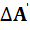) и работу сил, действующих на молекулы тела со стороны молекул окружающих тел. Последняя не сопровождается какими-либо макроскопическими движениями и называется количеством тепла, переданного телу (обозначает 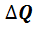). Если перейти к работе, выполняемой данным телом над внешними телами, 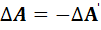, то

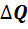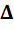= U + 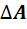, (6.1)

т.е. полученное телом тепло расходуется на изменение его внутренней энергии и выполнение им работы. Формула (6.1) называется первым законом термодинамики, который, по сути, является законом сохранения энергии.

Опыт показывает, что передача телу или полученное от него тепла сопровождается изменением его температуры, пропорциональным переданному или полученному количеству тепла:

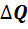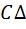= T(6.2)

где 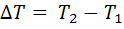– разность конечной и начальной температуры; С- теплоемкость тела, равная количеству теплоты, необходимому для нагревания его на 1 К.

Для одного тела теплоемкость прямо пропорциональна его массе m:

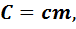(6.3)

где с - удельная теплоемкость вещества,из которого состоит тело. Она равна количеству теплоты, необходимому для нагревания единицы массы вещества на 1 К.

Теплоемкость одного моля вещества называют молярной теплоемкостью(обозначается ):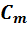

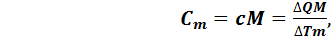(6.4)

где М –масса одного моля вещества. Эта масса в граммах численно равна массе молекулы в атомных единицах массы, т.е. она пропорциональна массе молекул. А значит, отношение массы моля к массе молекулы, равное числу молекул в одном моле, одинаково для веществ. Оно называется число Авогадро и равно: .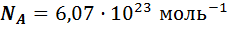

При вычислении внутренней энергии кристаллического твердого тела можно использовать принцип равнораспределения энергии по степеням свободы движения составляющих его атомов. Число степеней свободы атомов – это число независимых координат, которые можно задать положение атома в пространстве. На каждую классическую степень свободы атома приходится средняя кинетическая энергия теплового движения, равная:

, (6.5)

где 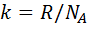- постоянная Больцмана, k=1,38·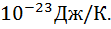

Тепловое движение атомов в кристаллическом твердом теле представляет из себя гармонические колебания относительно положений равновесия, которые являются узлами кристаллической решетки. Колебания могут осуществляться в трех перпендикулярных направлениях независимо друг от друга, соответственно для задания положения атома в пространстве требуется три независимые координаты.

Каждый атом кристалла имеет три колебательных степени свободы, и формула (6.5) определяет среднюю кинетическую энергию теплового движения, приходящуюся на каждую из них. Но атомы кристалла имеют также потенциальную энергию взаимодействия друг с другом, при характерных для кристалла расстояниях между атомами пренебрегать ею нельзя. В случае гармонических колебаний происходит переход кинетической энергии в потенциальную и обратно, причем суммарная полная механическая энергия не изменяется. Отсюда следует что характер изменений со временем у кинетической и потенциальной энергий должен совпадать, а значит, должны совпадать и их средние значения. Тогда средняя тепловая энергия, приходящаяся на одну колебательную степень свободы атома,

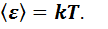(6.6)

Для получения внутренней энергии кристаллического твердого тела достаточно среднюю энергию ‹ε› умножить на число атомов тела 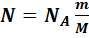и число колебательных степеней свободы атомов:

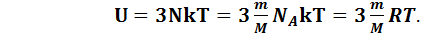(6.7)

Очевидно, что энергия одного моля вещества одинакова для всех кристаллических тел и равна:

(6.8)

Изменения внутренней энергии кристаллического твердого тела может быть связано только с изменением его температуры ΔT. Учтем также, что работа, выполняемая толом, ΔA= 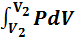и запишем первый закон термодинамики:

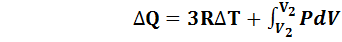.(6.9)

Изменение объема кристаллического твердого тела при изменении температуры настолько малы, что ими можно пренебречь и считать объем постоянным, а процесс изохорным. Это означает, что второе слагаемое в формуле (6.9) считается равным нулю и полученное телом количество тепла .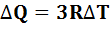

Подставляем это выражение в формулу для молярной теплоемкости тела (6.4) и получаем закон Дюлонга и Пти – молярные теплоемкости всех кристаллических тел одинаковы и равны:

(6.10)