Основные теоретические положения

ОПРЕДЕЛЕНИЕ УНИВЕРСАЛЬНОЙ ГАЗОВОЙ ПОСТОЯННОЙ

ЦЕЛЬ И МЕТОД РАБОТЫ

Определить численное значение универсальной газовой постоянной методом термостатирования.

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

На базе экспериментальных законов Бойля-Мариотта, Гей-Люссака, Шарля, Клапейрон установил, что для разреженных газов выполняется соотношение

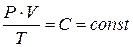, (1)

где P – давление газа (Па), V – объем газа (м³), T – абсолютная температура (К), C – газовая постоянная, зависящая от массы газа.

Соотношение (1) называют уравнением Клапейрона. Известно, что при нормальных условиях, т.е. при P=1 атм.=1,013×10⁵ Па и T=273 К один моль любого газа занимает один и тот же объем, равный
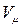=22,4 литра=2,24×10^{-2 м3}, поэтому для одного моля газа из соотношения (1) получаем:

,

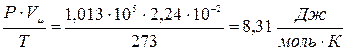или ,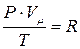

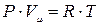, (2)

где величина R=8,31 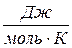одинакова для всех газов и называется молярной газовой постоянной или универсальной газовой постоянной.

Для произвольной массы m газа его объем V можно записать в виде:

,

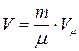откуда 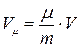, (3) где 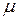- масса одного моля газа (кг/моль); 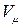- объем одного моля газа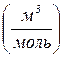

Подставляя соотношение (3) в (2) получим:

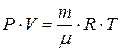(4)

Уравнение (4) называется уравнением Клапейрона-Менделеева. Оно справедливо для реальных газов при давлениях, существенно не превосходящих атмосферное, и для так называемых идеальных газов. Идеальным газом называется газ, между молекулами которого отсутствуют силы взаимного притяжения и отталкивания, а сами молекулы имеют пренебрежимо малый объем. Идеальный газ определяется требованием подчинения законам Бойля-Мариотта, Гей-Люссака и Шарля.

Состояние газа или системы характеризуется параметрами состояния, т.е. значениями P, V и T. Если параметры состояния не изменяются бесконечно долгое время, то состояние называется равновесным. Переход газа (или системы) из одного равновесного состояния с параметрами P₁ , V₁ и T₁ в другое равновесное состояние с параметрами P₂, V₂ и T₂ называется процессом. Если процесс состоит из последовательности равновесных промежуточных состояний, то процесс называется равновесным.

Процесс, происходящий при постоянном давлении P=const,называется изобарическим.

Процесс, происходящий при постоянной температуре T=const, называется изотермическим.

Процесс, происходящий при постоянном объеме V=const, называется изохорическим.

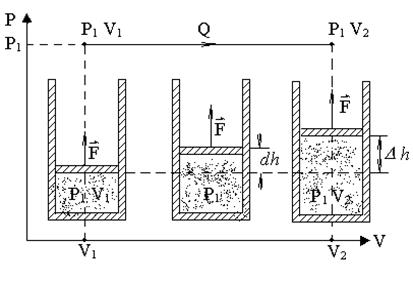
Рассмотрим изобарический процесс расширения газа из состояния P₁, V₁ и T₁ в состояние P₂ , V₂ и T₂ (рис.1). Представим себе газ, заключенный в цилиндр с поршнем, движением которого изменяется объем газа. Будем считать, что движение поршня происходит без трения. Площадь поршня равна S. 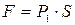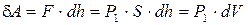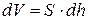Сила F, создаваемая давлением P₁ газа на поршень площади S, равна и, следовательно, работа, совершаемая газом при перемещении поршня на величину dh, равна , где - изменение объема газа.

Условились считать, что работа, произведенная газом при увеличении его объема, имеет положительный знак, а работа произведенная внешними силами над газом, имеет отрицательный знак.

Работа изобарического расширения газа из состояния P₁, V₁, T₁ в состояние P₂ , V₂ , T₂ определяется интегралом

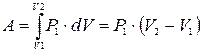. (5)

Так как при расширении газа объем увеличивается, то для сохранения постоянства давления к газу необходимо подводить теплоту Q.

Объем газа V₁ в начальном состоянии согласно уравнения (4), равен

Рис. 1 Изобарический процесс расширения газа в координатах PV.

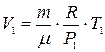, (6)

а объем газа V₂ в конечном состоянии будет равен

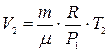. (7)

Из уравнений (6) и (7) получаем

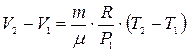. (8)

Подставив выражение (8) в уравнение (5) будем иметь:

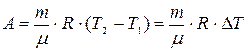. (9)

Если масса газа m равна массе одного моля газа m, а в процессе изобарического расширения температура газа увеличилась на 1К, т.е. 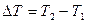=1К, то из уравнения (9) мы получим

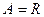(10)

Таким образом, универсальная газовая постоянная R численно равна работе, совершаемой одним молем идеального газа при изобарическом расширении вследствие нагревания на один Кельвин.

ВЫВОД РАБОЧЕЙ ФОРМУЛЫ

В результат проведения лабораторной работы известны:

1. Объем воздуха в сосуде V.

2. Атмосферное давление P.

3. Плотность воздуха в сосуде r.

4. Изменение объема DV воздуха в сосуде в результате изменения температуры воздуха на величину DT при P=const.

Рассчитать универсальную газовую постоянную.

При расширении воздуха в условиях P=const, работа, совершаемая воздухом равна

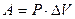, (11)

где 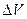- изменение объема воздуха при расширении.

Приравнивая правые и левые части уравнений (9) и (11), получим

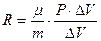, (12)

где - изменение температуры воздуха в сосуде; m - масса воздуха в сосуде.

Изменение объема 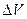воздуха можно определить по изменению уровня жидкости в левом колене манометра (см. рис. 2), вызванное расширением воздуха при его нагреве:

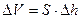, (13)

где S – площадь поперечного сечения трубки манометра;

- изменение уровня жидкости в левом колене манометра, взятое по шкале в мм.

Массу m воздуха в сосуде можно определить по плотности r воздуха, взятой из таблиц в зависимости от температуры и давления при начальных условиях опыта, т.е.

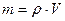. (14)

С учетом (13) и (14) из уравнения (12) получим

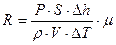- рабочая формула.

Величина 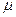для воздуха равна 29 10^-3 .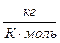