Упражнение 1 (собирающая линза)

Способ 1

№	а, м	b, м	f, м	<f>, м	< D >, дптр	Df, м	<Df>, м	df, %

Способ 2

№	b, м	АВ, м	А1В1,м	f , м	<f>, м	< D>, дптр	Df , м	<Df>, м	df, %

Упражнение 2 (рассеивающая линза)

№ п/п	а, м	b, м	f, м	<f>, м	< D>, дптр	Df, м	<Df>, м	df, %

Контрольные вопросы

1. Что называется линзой?

2. Какие бывают линзы?

3. Основные характеристики линзы.

4. Дайте определение фокуса линзы и главного фокусного расстояния линзы, проиллюстрируйте рисунком.

5. Что называется оптической силой линзы и какова единица ее измерения в СИ? Оптическая сила для собирающей и рассеивающей линз.

6. Построить изображение предмета в собирающей линзе, если предмет находится на расстояниях от линзы: а < f ; а = f ; а > f, охарактеризовать полученные изображения.

7. Построить изображение предмета в рассеивающей линзе, если предмет находится на расстояниях от линзы: а₁ < f₁ ; а = f₁ ; а₁ > f₁, охарактеризовать полученные изображения.

8. Формула собирающей и рассеивающей линз.

Литература

1. Трофимова Т. И. Курс физики. М.: Высш. шк., 1994. Часть 5, гл. 21, § 166.

2. Савельев И. В. Курс общей физики. М.: Наука, 1977. Том 2, часть 3, гл. XVI,

§ 115-117.

3. Грабовский Р. И. Курс физики. С-Пб.: Лань. 2002. Часть П, гл. VI, § 47.

ЛАБОРАТОРНАЯ РАБОТА № 4–06

ОПРЕДЕЛЕНИЕ ДЛИНЫ СВЕТОВОЙ ВОЛНЫ

С ПОМОЩЬЮ КОЛЕЦ НЬЮТОНА

Цель работы: изучение явления интерференции света в тонких пластинках, изучение установки для наблюдения колец Ньютона, определение длины световой волны с помощью колец Ньютона.

Приборы и принадлежности: плоскопараллельная пластинка, плосковыпуклая линза, микроскоп, осветитель, светофильтры.

Теория работы

Свет, с точки зрения классической электродинамики, представляет собой поперечные электромагнитные волны, распространяющиеся в вакууме со скоростью

с = 3×10⁸ м/с. Белый свет является совокупностью различных монохроматических волн. Существуют различные методы определения длин монохроматических волн. Одним из них является метод определения длины световой волны с помощью колец Ньютона.

Пусть выпуклая поверхность плосковыпуклой линзы с большим радиусом кривизны R соприкасается в некоторой точке с плоской поверхностью хорошо отполированной плоскопараллельной пластинки так, что оставшаяся между ними воздушная прослойка постепенно утолщается от точки соприкосновения к краям линзы (рис. 1).

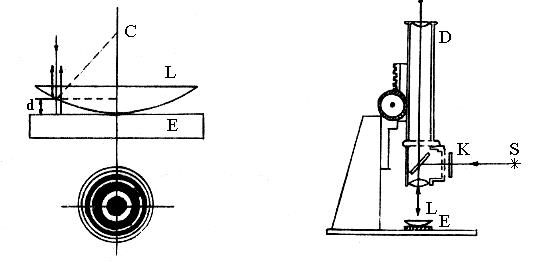Рис. 1 Рис. 2

Если такую систему осветить пучком монохроматического света, то световые волны, отраженные от нижней поверхности линзы и верхней поверхности пластинки будут интерферировать между собой. При этом образуется интерференционная картина, имеющая вид концентрических чередующихся cветлых и темных колец убывающей ширины. При отражении лучей от нижней пластинки, представляющей оптически более плотную среду, чем воздух, волны меняют фазу на противоположную, что эквивалентно изменению пути на l/2. В месте соприкосновения линзы с пластинкой остается тонкая воздушная прослойка, толщина d которой значительно меньше длины волны. Поэтому разность хода между лучами, возникающими в этой точке, определяется лишь потерей полуволны 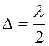при отражении от пластинки; следовательно, в отраженном свете в центре интерференционной картины наблюдается темное пятно. Если между линзой L и пластиной E находится воздух (n = 1) и пучок света падает нормально к пластине (a = 0) и практически нормально к нижней поверхности линзы (кривизна линзы мала), то разность хода в этом случае будет равна: .

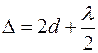Условие минимума интерференционной картины: 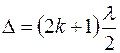, максимума: 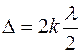, где k – целое число, называемое порядком интерференции.

Условие возникновения темных колец для отраженных лучей будет выражено уравнением:

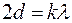(1)

Величина d может быть выражена через радиус R кривизны линзы и радиус r темного интерференционного кольца. Действительно, из рис. 1 находим, что .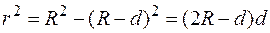

Eсли d мало по сравнению с R, то

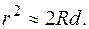(2)

Сравнивая выражения (1) и (2), получим:

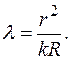(3)

Однако формула (3) не может быть применена для опытной проверки, поскольку невозможно добиться идеального соприкосновения линзы и плоской пластинки из–за упругой деформации стекла и частичек пыли. Формула, пригодная для определения длины волны монохроматического света, может быть получена, если вычислить l по разности радиусов двух колец r_m и r_k:

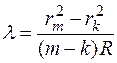, или окончательно: 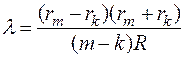. (4)

Таким образом, зная радиус кривизны R и радиусы r_m и r_k темных интерференционных колец, можно вычислить длину l световой волны.

Установка, применяемая в данной работе, изображена на рис. 2, где S - источник света (электрическая лампочка накаливания); K - светофильтр, пропускающий свет, длина волны которого подлежит измерению; M - полупрозрачная пластина; E - стеклянная пластина, на которой лежит плосковыпуклая линза L; D – микроскоп с окулярной шкалой. Падающие на полупрозрачную пластинку M монохроматические лучи, отражаясь и проходя через линзу L, попадают на пластинку E. Интерференционная картина рассматривается в микроскоп. Глядя в окуляр микроскопа, наблюдатель будет видеть в увеличенном виде кольца Ньютона. С помощью окулярного микрометра можно определить радиусы этих колец.