Методика проведения эксперимента. Лабораторная работа 1.5

Лабораторная работа 1.5.

Определение вязкости воздуха методом истечения из капилляра.

Цель работы:

1. Исследовать явление вязкости газов;

2. Изучить метод определения коэффициента динамической вязкости, основанный на истечении газа из капилляра.

3. Определить по полученным данным коэффициент динамической вязкости воздуха, длины свободного пробега молекул и числа Рейнольдса.

Требуемое оборудование:

1. Электронный блок БЛТ2

2. Измерительная камера для БЛТ2

Краткая теория

Рассматривая протекающие в газах процессы, мы использовали понятие идеального газа. Идеальная жидкость, т.е. жидкость без трения, является абстракцией. Всем реальным жидкостям и газам в большей или меньшей степени присуща вязкость или внутреннее трение. Вязкость проявляется в том, что возникшее в жидкости или газе движение после прекращения действия причин, его вызвавших, постепенно прекращается.

Состояние движения жидкости можно определить, указав для каждой точки пространства вектор скорости как функцию времени. Величина и направление вектора в каждой точке могут меняться со временем. Если вектор скорости в каждой точке пространства остается постоянным, то течение называется установившимся или стационарным. При стационарном течении любая частица жидкости проходит данную точку пространства с одним и тем же значением скорости.

Основное положение молекулярно-кинетической теории сводится к тому, что молекулы газа движутся хаотически. Скорость движения молекул определяет тепловое состояние газа. В процессе своего движения молекулы соударяются друг с другом и со стенками сосуда. Траектория движения частиц является зигзагообразной, состоящей из отдельных прямолинейных отрезков пути (между соударениями). Средней длиной свободного пробегамолекулы λ называется среднее расстояние, проходимое молекулой между последовательными столкновениями ее с другими молекулами.

Рассмотрим направленное движение газа по трубе круглого сечения. Молекулы газа участвуют одновременно в двух движениях: хаотическом тепловом и направленном. Молекулы, оказавшиеся вблизи стенки, сталкиваются со стенкой, теряют свою энергию и замедляются. За счет теплового движения они переходят в близлежащие слои газа и замедляют их. Вследствие этого скорости направленного движения молекул оказывается различными в разных точках поперечного сечения трубы. Наибольшей скоростью движение совершается в средней части сечения трубы (рис.1), а по мере приближения к стенкам скорость убывает.

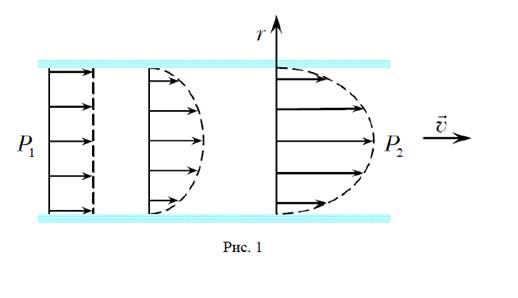
Весь поток газа можно мысленно разбить на слои цилиндрической формы, движущиеся с различными скоростями. Все молекулы газа, помимо направленного движения, участвуют в тепловом движении, поэтому происходит непрерывный переход молекул из более быстрого слоя в более медленный слой и обратно. В результате столкновения молекулы обмениваются импульсами. Это приводит к возникновению между слоями, испытывающими относительное перемещение, силы внутреннего трения. Сила внутреннего трения направлена по касательной к границе между слоями и стремится уравнять скорости движения разных слоев. Свойства газа, связанные с наличием сил внутреннего трения, называют вязкостью или внутренним трением.

Сила внутреннего трения между слоями равна:

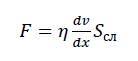
где S_сл – площади соприкосновения слоев; v – скорость направленного движения газа; dv/dx - градиент скорости; η – коэффициент пропорциональности, зависящий от рода газа (жидкости), от температуры среды и называемый коэффициентом динамической вязкости.

Величиной, характеризующей скольжение слоев друг относитель­но друга, является градиент скорости, равный: .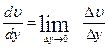

Эта величина показывает изменение скорости слоев жидкости, отнесенное в единице длины в направлении, перпендикулярном рассматриваемым слоям (от слоя к слою).

Коэффициент динамической вязкости численно равен силе внутреннего трения, действующей на единичные площади соприкосновения параллельно движущихся слоев газа (жидкости) при единичном градиенте скорости между ними. Единицей вязкости в СИ является Па·с.

Наблюдается два вида течения жидкости (или газа). Если жидкость как бы разделена на слои, которые скользят друг относительно друга, не перемешиваясь, то течение называется ламинарным. Если в такой поток ввести подкрашенную струйку, то она сохранится, не размываясь по всей длине потока, так как в ламинарном потоке частицы жидкости не переходят из одного слоя в другой. Ламинарное течение стационарно.

При увеличении скорости потока может наблюдаться перемешивание слоев жидкости. Такое движение называется турбулентным. При турбулентном течении скорость частиц в каждом данном месте все время изменяется беспорядочным образом – течение нестационарное. Если в турбулентный поток ввести окрашенную струйку, то уже на небольшом расстоянии от места ее введения окрашенная жидкость равномерно распределится по всему сечению потока.

При ламинарном течении в пределах слоя скорость направленного движения остается постоянной. Для цилиндрической трубы круглого сечения на некотором расстоянии от конца трубы устанавливается стационарное распределение скоростей по параболическому закону:

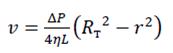
где ΔP – перепад давления на концах трубы, L – длина трубы, R_Т – радиус трубы, r – радиальная координата.

Если газ считать идеальным, то из молекулярно-кинетической теории можно получить выражение для коэффициента динамической вязкости:

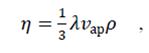(1)

где v_ар – средняя арифметическая скорость теплового движения молекул, равная:

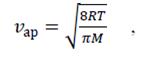(2)

где R – универсальная газовая постоянная, T – абсолютная температура газа, M – молярная масса газа

Объем газа, протекающего через поперечное сечение трубы в единицу времени называется расходом Q. При ламинарном течении газа по цилиндрической трубе круглого сечения расход можно определить формуле Пуазеля как:

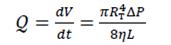(3)

Если перепад давления увеличивается, скорость течения растет, и движение газа из ламинарного переходит в турбулентное, при котором скорости частиц изменяются беспорядочным образом, слои перемешиваются, образуются завихрения (рис. 2).

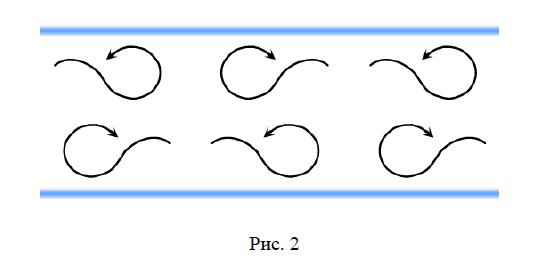
Для оценки изменения характера движения газа (жидкости) используют безразмерную величину, называемую числом Рейнольдса:

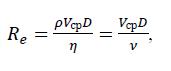(4)

где ρ – плотность среды; V_ср – средняя скорость течения; D – характеристический размер (например, диаметр трубы); ν=η/ρ – коэффициент кинематической вязкости.

Учитывая по формуле (3), что

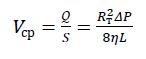
где S – площадь поперечного сечения трубы.

Число Рейнольдса для случая цилиндрической трубы можно рассчитать по формуле:

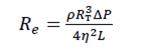(5)

При движении газа в круглой трубе течение является ламинарным, если R_e < 1000

Методика проведения эксперимента

Рассмотрим экспериментальную установку, состоящую из баллона объемом V0, к которому через клапан подсоединен капилляр. В баллон заканчивается воздух, затем открывается кран, и воздух из баллона вытекает через капилляр в атмосферу. При этом давление в баллоне уменьшается, и перепад давления на концах капилляра ΔP=P-P_атм также непрерывно убывает.

Перепад давления будет зависеть от времени истечения воздуха из капилляра:

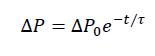(6)

где ΔP₀ – перепад давления в начальный момент времени t=0; τ – время релаксации, т.е. время, за которое начальный перепад давления убывает в е раз.

Продифференцировав это уравнение по времени, получим:

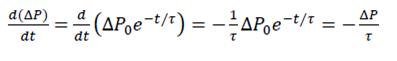(7)

Логарифмируя (6), получим уравнение:

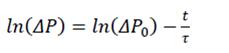(8)

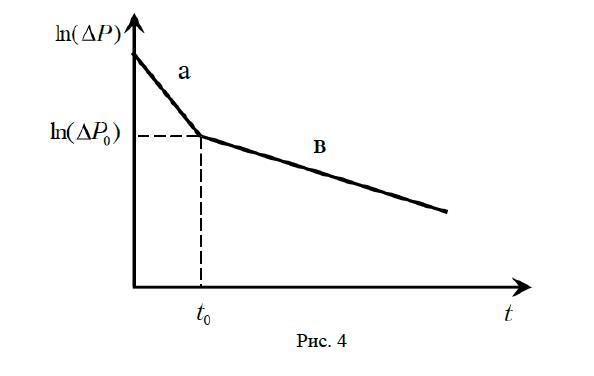
из которого следует, что график зависимости ln(ΔP) от t – прямая линия.

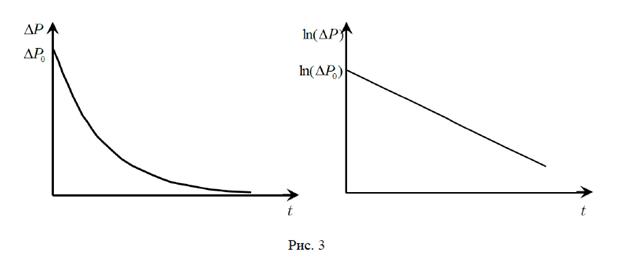
Истечение воздуха из баллона через капилляр можно рассматривать как процесс изотермического расширения газа с постоянной массой.

Тогда согласно уравнению Менделеева-Клайперона: PV=const. Продифференцировав это уравнение по времени, получим:

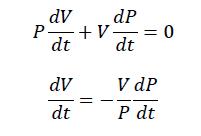
Учтем, что

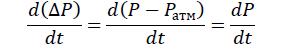
получим, используя (3), (7)

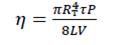
Поскольку можно принять P≈P_атм и V≈V₀ (итоговая ошибка не более 20%), то

(9)

Полученная рабочая формула верна только для ламинарного течения газа. Если на графике зависимости ln(ΔP) от t наблюдается излом, то это означает, что при высоких перепадах ΔP режим течения является турбулентным (участок “а” на рис.4). По этому, в дальнейших расчетах следует использовать только данные участка «в».

Все измерения проводятся при помощи блока для определения термодинамических характеристик воздуха БЛТ2. Этот блок позволяет определять:

1) показатель адиабаты воздуха γ;

2) динамическую вязкость воздуха методом истечения из капилляра.

Блок состоит из двух модулей:

1) электронный блок;

2) измерительная камера.

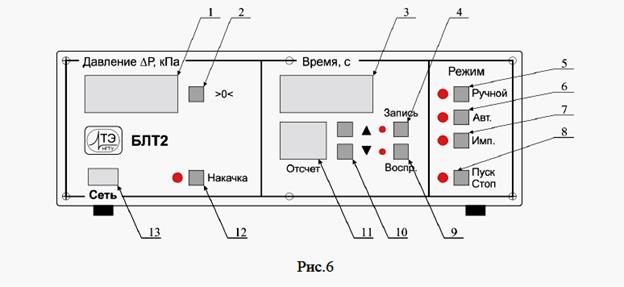
На передней панели электронного блока БЛТ2 (рис.6) расположены:

1 – индикатор давления;

2 – кнопка коррекции нуля; 3 – секундомер;

4 – кнопка «Запись»;

5 – кнопка выбора режима «Ручной»;

6 – кнопка выбора режима «Автоматический»;

7 – кнопка выбора режима «Импульсный»;

8 – кнопка выбора «Пуск/Стоп»;

9 – кнопка «Воспроизведение»;

10 – кнопки выбора отсчетов;

11 – индикатор выбора отсчетов;

12 – кнопка включения компрессора «Накачка».

13 – кнопка выключателя «Сеть». Измерительная камера представлена на рис.7:

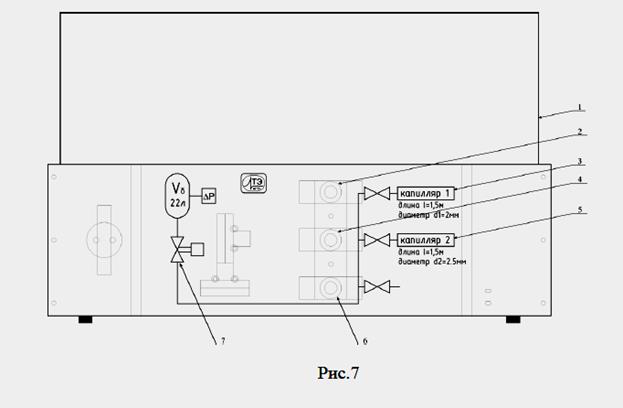
1 – измерительная камера;

2 – вентиль для соединения капилляра 1;

3 – капилляр 1;

4 – вентиль для соединения капилляра 2;

5 – капилляр 2;

6 – вентиль для выравнивания давления в камере с атмосферным;

7 – электромагнитный клапан.

Давление воздуха в камере контролируется дифференциальным датчиком давления, соединенным с камерой трубкой. Измерения показателя адиабаты производятся в импульсном режиме «Авт.». Ниже представлен алгоритм работы электронного блока БЛТ2 в этом режиме.

1. После нажатия кнопки «Пуск», записывается в память начальное значения давления и открывается ЭМ клапан.

2. Через каждые 0,3 кПа происходит запись очередных отсчетов давления и времени в автоматическом режиме.

3. После повторного нажатия кнопки «Пуск» прибор переходит в режим ожидания

4. Просмотр отсчетов записей осуществляется в режиме ожидания. Для начала просмотра нажмите кнопку «Воспроизведение» 9. С помощью кнопок выбора отсчѐтов 10 и индикатора 11 осуществляется просмотр записей.