Взаимодействие электромагнитного излучения и вещества

Исследование взаимодействия излучения и вещества представляет собой одну из центральных проблем астрофизики.

Во-первых, почти вся получаемая нами информация о физических свойствах небесных тел содержится в их излучении.

Во-вторых, сами свойства этих тел, их структура и динамика определяются наряду с гравитацией также и трансформацией лучистой энергии в этих телах. Возможность конденсации космической среды в более плотные объекты - звезды, сама структура звезды и ее эволюция, строение и особенности поведения межзвездного газа - все это в той или иной мере зависит от переноса лучистой энергии в веществе.

В этом параграфе мы проведем анализ ряда основных формул, знакомых каждому астрофизику, и получим соотношения, которые нам понадобятся в дальнейшем для анализа методом размерностей других задач.

Начнем с хорошо известной формулы Планка для интенсивности термодинамически равновесного излучения

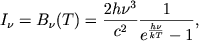(2.32)

где частота &nu = &omega/2&pi и постоянная Планка h = 2&piħ.

Зная размерности величин, входящих в формулу (2.32), можно построить матрицу размерности:

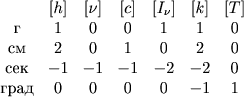У нас шесть параметров при четырех первичных величинах, так что согласно П-теореме должно быть два безразмерных комплекса. Два из показателей степеней можно выбрать произвольно; полагая показатель при I_&nu равным единице, а показатель при постоянной Планка - нулю, получим первый безразмерный комплекс

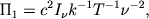(2.33)

Для нахождения второго комплекса примем показатель при I_&nu равным нулю, а показатель при постоянной Планка - единице. Получим

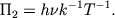(2.34)

Тогда формула Планка запишется в виде зависимости безразмерного комплекса П₁ от комплекса П₂:

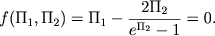(2.35)

Конкретный вид функции &fnof(П₁, П₂) определен не методом размерностей, однако даже суждение об аргументах функций, получаемых посредством размерностной процедуры, часто оказывается достаточным для многих целей. В том случае, когда один из безразмерных комплексов мал (например, в радиодиапазоие П₂ << 1), из условия &fnof(П₁, П₂) = 0 следует, что П₁ = const, а из явного вида этой функции получаем, что П₁ = 2. Отсюда имеем закон Рэлея - Джинса:

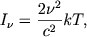(2.36)

который, кстати, первоначально и был получен из соображений размерности. Если П₂ не мало, то, разумеется, однозначной формулы из одних соображений размерности не получить.

При произвольных значениях П₁ и П₂ эти комплексы могут служить критерием подобия. Известно, что спектральные кривые распределения энергии имеют максимум. Критерий подобия означает, что максимумы излучения при разных температурах соответствуют одним и тем же значениям безразмерных комплексов, а именно П₂ = 2,82, П₁ = 0,35. Это есть известный закон смещения Вина:

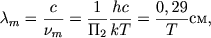(2.37)

если температура выражена в градусах. В (2.37) и последующих формулах интенсивность излучения отнесена к единичному интервалу частот - весь анализ нетрудно провести и в случае, когда спектральная интенсивность отнесена к единичному интервалу длин волн. В этом случае изменится определение безразмерного комплекса П₁ но функция &fnof(П₁, П₂) будет иметь прежний вид. Несколько сместится и положение максимума в законе Вина (2.37).

Другое хорошо известное в астрофизике соотношение - формула Саха - определяет степень ионизации. Если через n_s, n_e и n₁обозначить концентрацию атомов, электронов и ионов данного элемента, то формула Саха записывается в виде

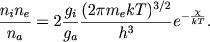(2.38)

Здесь &chi - потенциал ионизации, g_a и g_i - статистические веса атома и иона. Ограничимся случаем водорода и примем в дальнейшем g_a = g_i = 2 (для основного состояния).

Чтобы записать уравнение Саха с помощью безразмерных комплексов, вспомним определение дебройлевской длины волны электрона &lambda = h/m_ev, где v - его скорость. У тепловых электронов скорость пропорциональна (kT/m_e)^½ и поэтому для них

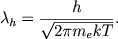(2.39)

Теперь определим следующие безразмерные комплексы:

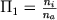- отношение концентрации ионов к концентрации атомов;

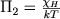- отношение энергии ионизации к тепловой энергии частиц;

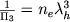- количество электронов в ячейке пространства с размером, равным дебройлевской длине волны.

Очевидно, что комплекс П₃ характеризует количество электронов, способных оказаться вблизи атома или иона и участвовать в процессах ионизации и рекомбинации.

С определенными выше безразмерными комплексами формула Саха записывается в очень простом виде:

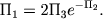(2.40)

Можно привести и другие примеры записи хорошо известных астрофизических формул в виде соотношений между безразмерными комплексами.

Если отнести коэффициент поглощения или рассеяния к одному атому, иону или электрону, то такую величину принято называть эффективным сечением и обозначать буквой &sigma_&nu. Ее размерность

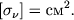(2.41)

Умножив эффективное сечение на число поглощающих или рассеивающих частиц в единице объема, получим коэффициент поглощения k_&nu, рассчитанный на единицу длины. Поэтому его размерность

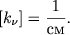(2.42)

И наконец, относя коэффициент поглощения к единице плотности, получим величину коэффициента непрозрачности 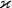с размерностью

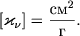(2.43)

Строго говоря, переход от (2.41) к (2.42) и (2.43) не сводится к простому умножению на концентрацию или делению на плотность.

Простейшим механизмом взаимодействия излучения и вещества является томсоновское рассеяние света на свободных электронах. Здесь эффективное сечение не зависит от частоты:

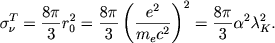(2.44)

Определение входящих сюда величин дано в § 5 гл. 1. Выражение 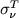через комптоновскую длину волны &lambda_K и постоянную тонкой структуры а нам понадобится для сравнения с другими механизмами.

Коэффициент непрозрачности при томсоновском рассеянии равен

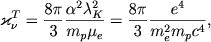(2.45)

где &mu_K - молекулярный вес, приходящийся на один свободный электрон. Существенно, что выражение (2.45) постоянно и за исключением множителя ц.е зависит только от мировых констант.

Следующий "по сложности" механизм - поглощение или рассеяние электромагнитных волн при переходах электрона между дискретными состояниями атомов или ионов. Обозначим через v0 частоту перехода.

В этом механизме эффективное сечение существенно зависит от частоты. Оно достигает максимума на частоте перехода и быстро спадает в обе стороны с ростом разности |&nu - &nu₀|, где &nu - частота рассеиваемой или поглощаемой волны. Формула для эффективного сечения:

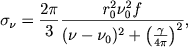(2.46)

где &fnof есть сила осциллятора, безразмерный множитель, показывающий, насколько процесс рассеяния при переходах в атоме отличается от такого же перехода в случае рассеяния света классическим осциллятором. Величина

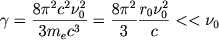(2.47)

есть так называемая естественная ширина линии. Максимум эффективного сечения в центре линии (&nu = &nu₀) очень велик:

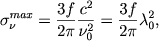(2.48)

но быстро спадает при |&nu - &nu₀| >> &gamma . При |&nu - &nu₀|, сравнимым с &nu₀, эффективное сечение (2.46) даст примерно столько же, сколько томсоновекое сечение.

Формулы (2.44), (2.48) и другие последующие формулы наглядно показывают, что эффективное сечение должно представлять собой произведение двух параметров с размерностью длины. В случае (2.44) это было r₀, в случае (2.48) мы получили &lambda₀- длину волны, в остальных случаях будут встречаться и другие комбинации.

Существенно больший вклад в коэффициент поглощения вносят переходы из связанного состояния в свободное, т. е. ионизация атомов и ионов. Запишем эффективное сечение для поглощения с первого уровня атома водорода:

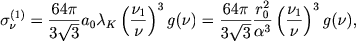(2.49)

где &nu₁=&chi_H/h - частота порога ионизации, g(&nu) - очень медленно меняющаяся безразмерная функция частоты. Вблизи порога при &nu = &nu₁ g(&nu₁)=0,80, а среднее значение этой величины по спектру примерно равно 0,89. Формулы, аналогичные (2.49), получаются и для других уровней как атома водорода, так и других атомов. Здесь меняется численный коэффициент и, вообще говоря, оказывается более сложная зависимость от частоты.

Эффективное сечение (2.49) в максимуме при &nu = &nu₁ очень велико. Сравнивая (2.49) с томеоновеким сечением (2.47), получим

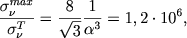(2.50)

но при усреднении по частотам это различие, естественно, заметно уменьшается. Имеем для сечения, отнесенного к одному атому:

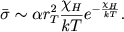(2.51)

При усреднении принято, что распределение энергии в спектре излучения описывается формулой Планка, а распределение по состояниям - уравнением Больцмана.

Величину r_T с размерностью длины

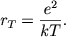(2.52)

можно было бы назвать "тепловым радиусом электрона", по аналогии с классическим радиусом электрона r₀ = e²/m_ec². Очевидно, что чем больше температура, тем быстрее движутся электроны и тем меньше вероятность их взаимодействия с атомами.

Следующий важный механизм взаимодействия излучения и вещества - это поглощение в непрерывном спектре при так называемых свободно-свободных переходах. Среднее эффективное сечение этого процесса, уже усредненное по максвелловской функции распределения скоростей электронов и по планковскому спектру излучения и отнесенное к одному иону, имеет вид:

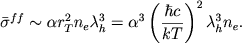(2.53)

Учитывая уравнение Саха, можно убедиться, что при высоких температурах (Т &ge 3 &sdot 10⁵ град) свободно-свободные переходы оказываются определяющими.

Переходя от 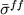к коэффициенту непрозрачности

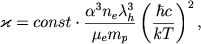получим хорошо известную формулу Крамерса, которую обычно записывают в виде

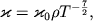(2.54)

где размерный коэффициент 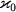пропорционален следующему набору фундаментальных постоянных:

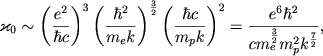(2.55)

Его размерность

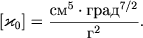(2.56)

Кроме фундаментальных атомных постоянных в k₀ входят безразмерные множители, зависящие от состояния ионизации вещества и его химического состава.

На низких частотах, например, в радиодиапазоне, также преобладает поглощение при свободно-свободных переходах. Эффективное сечение, усредненное по маковелловскому распределению скоростей и учитывающее индуцированные процессы, имеет вид

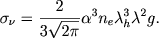(2.57)

Здесь &lambda - длина поглощаемой волны и g - множитель Гаунта, логарифмически зависящий от температуры и концентрации электронного газа. Формула (2.57) используется в радиоастрономии, где коэффициент поглощения обычно относят не к единице плотности, а к единице объема, и поэтому имеем

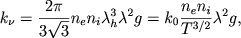(2.58)

где

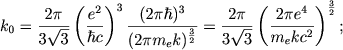(2.59)

а множитель Гаунта соответствующей области частот космического радиоизлучения

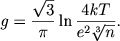(2.60)

Размерность параметра k₀ есть

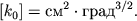(2.61)

Механизмы поглощения всегда связаны и с механизмами излучения. В частности, обратным механизму поглощения, описываемого сечением (2.49), является процесс рекомбинации, при которой электрон, попадая на атомный уровень, излучает квант электромагнитной волны. Выражение для эффективного сечения рекомбинации при попадании электрона сразу на первый уровень есть

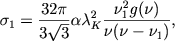(2.62)

где g(&nu) - тот же множитель Гаунта, что и в (2.49), и &nu₁ - по-прежнему частота порога ионизации.

Величина h(&nu - &nu₁) есть энергия рекомбинирующего электрона, и поэтому для получения коэффициента рекомбинации в единице объема следует (2.62) усреднить по максвелловской функции распределения скоростей. В результате получим, что полное число рекомбинаций в единице объема, пропорционально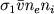е где 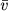- средняя скорость электронов, записывается в виде

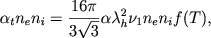(2.63)

где &fnof(T) - некоторая безразмерная функция, слабо зависящая только от температуры.

Основным параметром, характеризующим число рекомбинаций, есть величина &alpha_t с размерностью

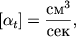(2.64)

уже использованная в формулах (1.34) - (1.36) . В соответствии со своей размерностью, эта величина состоит из произведения куба дебройлевокой длины волны и частоты излучения. Дело в том, что всегда рекомбинация происходит с участием трех тел (одно из них - фотон) - это необходимо для одновременного выполнения законов сохранения энергии и импульса.

Из (2.64) следует и зависимость &alpha_t от температуры. Если пренебречь функцией &fnof(T), то &alpha_t &sim T^-3/2; более точный учет разных зависимостей дает &alpha_t &sim T^-1,3.

В исследовании межзвездной среды большое значение имеет определение эффективных сечений возбуждений атомов электронным ударом. Обычно их записывают в виде

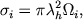(2.65)

где &lambda_h, по-прежнему, определено формулой (2.39), а безразмерная величина &Omega_i (порядка единицы) называется "силой электронного удара".

Заключение

В заключение этого раздела заметим, что с помощью теории анализа размерностей можно исследовать и взаимодействие излучения с гравитационными полями (в частности и в рамках общей теории относительности). Особенность здесь в том, что и электромагнитное поле и поля гравитации описываются не скалярными величинами, а тензорами. Поэтому приходится находить не безразмерные комплексы, а безразмерные скаляры, составленные из тензорных величин. Пример такого расчета был приведен в работе Н. Р. Сибгатуллина [5], где была оценена длина пути заметного уменьшения интенсивности электромагнитной волны из-за взаимодействия с собственным магнитным полем. Электромагнитный тензор пропорционален произведению компонент электромагнитного поля в волне E_iE_j &sim E²; гравитационное поле определяется параметрами G ис. Составив из параметров E², G и с величину с размерностью длины, найдем расстояние заметного гравитационного затухания электромагнитной волны

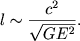(2.66)

Для обычных электромагнитных волн от астрофизических объектов длина их гравитационного затухания очень велика.

Список литературы

1. Физика. Большой энциклопедический словарь/Гл. ред. А. М. Прохоров. — 4-е изд. — М.: Большая Российская энциклопедия, 1999. — С. 874—876. ISBN 5-85270-306-0 (БРЭ)

2. Кудряшов Ю. Б., Перов Ю. Ф. Рубин А. Б. Радиационная биофизика: радиочастотные и микроволновые электромагнитные излучения. Учебник для ВУЗов. — М.: ФИЗМАТЛИТ, 2008. — 184 с — ISBN 978-5-9221-0848-5

3. Физический энцеклопедический словарь

4. Г.Е.Зильберман. Электричество и магнетизм.М."Наука" 1970.