Краткое теоретическое введение

1. Индуктивность контура. Явление самоиндукции

Вокруг любого проводника с током I существует магнитное поле.

Собственное магнитное поле контура с током создает собственный магнитный поток 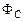через воображаемую поверхность S, ограниченную этим контуром,

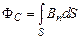, (15.1)

где 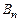– проекция вектора индукции 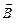магнитного поля тока I на нормаль к элементу поверхности dS.

Из закона Био–Савара–Лапласа и принципа суперпозиции следует, что эта проекция при постоянном значении магнитной проницаемос-
ти m равна

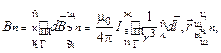
где 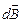– вектор индукции магнитного поля, созданного элементом 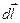замкнутого контура Гс током I в точке, местоположение которой относительно 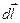определяется радиус – вектором .

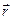Подставляя выражение для 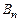в формулу (15.1) и вынося из-под знака интеграла постоянные, получаем

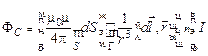(15.2)

или

.

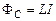Коэффициент пропорциональности 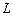между собственным потоком вектора магнитной индукции 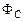через поверхность, ограниченную контуром, и силой тока 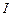в этом контуре называется индуктивностью контура (коэффициентом самоиндукции).

Из формулы (15.2) следует, что индуктивность контура зависит только от геометрических размеров, формы контура и магнитной проницаемости 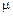той среды, в которой он находится.

Единица индуктивности в СИ называется Генри (Г):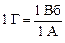

Для достаточно длинного соленоида, витки которого плотно прилегают друг к другу и сделаны из проводника с очень малым поперечным сечением, индуктивность выражается следующей формулой:

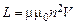, (15.3)

где 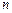– плотность намотки витков соленоида; 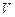– объем соленоида;
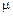– магнитная проницаемость вещества сердечника.

Если сила тока, протекающего по контуру, изменяется со временем, то в соответствии с законом Фарадея в контуре наводится ЭДС самоиндукции

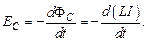
Если контур с током не деформируется и магнитная проницаемость среды 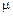не изменяется (нет ферромагнетиков в магнитном поле контура), то 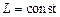и

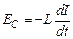. (15.4)

По правилу Ленца, ЭДС самоиндукции противодействует изменению тока в контуре, замедляя как его возрастание, так и убывание.

2. Закон изменения тока в цепи при подключении

и отключении источника.

Применение закона для определения индуктивности

Найдем изменение тока в цепи, состоящей из последовательно соединенных соленоида, индуктивность которой равна 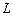, и резистора, активное сопротивление которого .

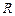Если внешнее магнитное поле отсутствует или постоянно, а контур неподвижен, то индукционные явления обусловлены только самоиндукцией.

Из закона Ома для замкнутой цепи, в которой действует источник ЭДС 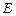, а общее активное сопротивление 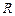, сила тока равна

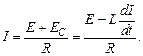
Для нахождения зависимости силы тока от времени разделим переменные

.

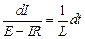Полагая 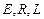постоянными и интегрируя, получаем

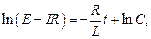
где 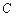– постоянная интегрирования, значение которой определяется начальными условиями решаемой задачи.

Пусть в момент времени 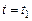сила тока 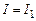. Тогда

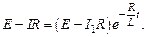
Выразив силу тока, получим

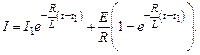(15.5)

Из этой общей формулы можно получить зависимость силы тока от времени при замыкании цепи. В этом случае начальный ток равен нулю 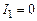и выражение (15.5) приобретает вид

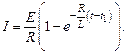(15.6)

Из этой формулы видно, что сила тока при замыкании цепи постепенно увеличивается, стремясь к 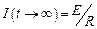, соответствующей величине постоянного тока (рис. 15.1). Нарастание тока происходит тем медленнее, чем меньше отношение 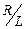в показателе степени экспоненты или больше обратное отношение 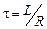, физический смысл которого обсуждается ниже.

Если же в момент времени 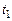при силе тока 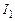источник ЭДС отключить ( 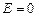), сохранив замкнутость цепи, то из формулы (15.5), получим следующую зависимость силы тока от времени:

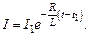(15.7)

В этом случае сила тока в цепи постепенно уменьшается от начального значения 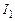, стремясь к нулю. При этом за время 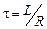(время релаксации) сила тока изменяется в 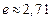раза.

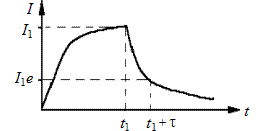
Рис. 15.1

Следует заметить, что в опыте удобнее снимать вместо зависимости силы тока в цепи от времени 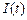зависимость напряжения на некотором известном активном сопротивлении 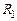, последовательно включенном в цепь, от времени 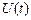. Напряжение в этом случае будет пропорционально силе тока.

Из сказанного ясно, что, измерив силу токов (или напряжения) в некоторые моменты времени 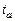, 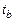и зная, кроме того, величину общего активного сопротивления контура 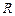, можно с помощью зависимостей (15.6) или (15.7) определить индуктивность контура .

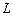Особенно просто, зная активное сопротивление цепи 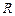, определить её индуктивность, измерив время релаксации,

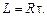(15.8)

3. Вынужденные электромагнитные колебания в контуре,

их применение для измерения индуктивности

Рассмотрим контур, состоящий из последовательно соединенных конденсатора емкостью 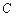, активного сопротивления 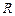и соленоида индуктивностью .

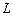Для получения незатухающих электромагнитных колебаний необходимо включить в контур источник тока с периодически изменяющейся ЭДС (рис. 15.2).

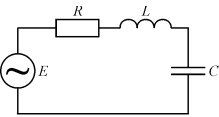
Рис. 15.2

В этом случае колебания в контуре являются вынужденными.

Пусть внешняя ЭДС изменяется по гармоническому закону

.

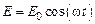Тогда, используя закон Ома, можно получить следующее дифференциальное уравнение вынужденных электромагнитных колебаний

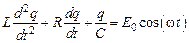
и, решив это уравнение, найти для установившихся вынужденных колебаний связь амплитудных значений силы тока и внешней ЭДС

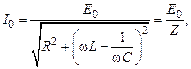(15.9)

где величина 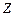называется полным сопротивлением электрической цепи переменного тока.

В нее входят активное сопротивление 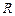контура, емкостное сопротивление 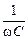и индуктивное сопротивление .

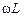Если электрическая емкость контура стремится к бесконечности 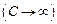, то есть емкостное сопротивление к нулю, то формула (15.9) упрощается

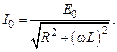(15.10)

Используя это выражение, получаем рабочую формулу для экспериментального определения индуктивности соленоида. При этом учтем, что амплитуда падения напряжения на активном сопротивлении R связана с амплитудой силы тока в цепи формулой

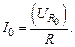(15.11)

Из выражений (15.10) и (15.11) получим

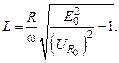(15.12)

Схемы измерений

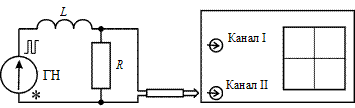
Рис. 15.3

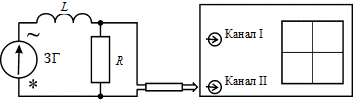
Рис. 15.4

Вариант 1. Оценка индуктивности соленоида

Задание к работе

1. Подключите последовательно соединенные резистор 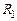и катушку индуктивности 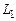без ферромагнитного сердечника к генератору прямоугольных импульсов (рис. 15.3).

2. Подключите Y-вход осциллографа к резистору 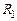. На генераторе установите частоту 1200 Гц. Получите на экране устойчивую картину изменения со временем, напряжения на этом сопротивлении, подобную изображенной на рис. 15.1 (см. Приложение).

3. Зная время развертки осциллографа, определите время релаксации 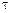, а затем по формуле (15.8) вычислите величину индуктивности 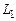. При этом общее сопротивление цепи R можно приближенно заменить значением 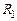, пренебрегая внутренним сопротивлением генератора и активным сопротивлением катушки. Поэтому полученное численное значение индуктивности следует рассматривать как оце-
ночное.

4. Повторите измерения 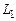, подключая другие резисторы. Проверьте, зависят ли получаемые значения индуктивности от сопротивления.

5. Приступите к измерению индуктивности вторым способом. Для этого подключите последовательно соединенные резистор 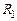и катушку индуктивности 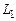к звуковому генератору (рис. 15.4), установив на нем некоторые значения частоты в диапазоне 5...15 кГц и амплитуды сигнала. (При таких частотах ток в цепи определяется в основном индуктивным сопротивлением катушки, что повышает точность измерения индуктивности.)

6. С помощью осциллографа измерьте амплитудное значение падения напряжения на резисторе .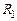

7. Отключите Y-вход осциллографа от резистора, а звуковой генератор от RL-контура и, не изменяя величину сигнала ЗГ, измерьте с помощью осциллографа амплитудное значение ЭДС генератора 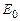(см. схему рис. 12.5).

8. Вычислите индуктивность по формуле (15.12).

9. Определите индуктивность, установив другие значения вели-
чин 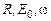. Проверьте, влияют ли эти параметры на результаты изме-рения.

10. Сравните результаты измерения индуктивности 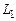двумя способами. Объясните различие этих результатов.

Вариант 2. Измерение индуктивности соленоида

Методика измерений

Рассмотрим более подробно первый способ определения индуктивности, основанный на измерении времени релаксации.

Учтем, что общее активное сопротивление контура R равно сумме известного сопротивления R₁ и неизвестного заранее сопротивления R^*, обусловленного внутренним сопротивлением генератора, сопротивлением соединительных проводов, сопротивлением провода катушки соленоида:

.

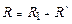С учетом этого перепишем формулу (15.7) в виде

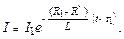(15.13)

Тогда время релаксации при подключении сопротивления R₁ можно записать как

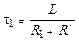. (15.14)

Это время можно измерить с помощью осциллографа и схемы, изображенной на рис. 15.3.

Если заменить сопротивление R₁ другим сопротивлением R₂, то время релаксации станет равным

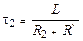. (15.15)

Рассматривая (15.14) и (15.15) как систему двух уравнений с двумя неизвестными R^* и L, находим

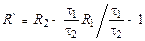, (15.16)

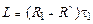или 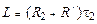. (15.17)

Формулы (15.17) позволяют, измерив 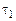и 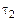, определить индуктивность соленоида с учетом 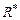, т. е. существенно повысить точность измерения.

Теперь рассмотрим второй способ определения индуктивности L соленоида с помощью вынужденных электромагнитных колебаний в контуре.

Учтем, что в формулу (15.10) входит общее сопротивление кон-
тура

,

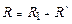а в формулу (15.11) – напряжение на сопротивлении R₁.

С учетом этого приравняем правые части формул (15.10) и (15.11)

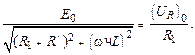(15.18)

Выражая из (15.18) индуктивность, получаем

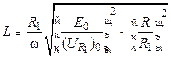. (15.19)

Формула (15.19) переходит в (15.12) при 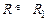, т. е. при условии 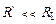. Кроме того, из (15.19) видно, что точность определения L растет с ростом отношения 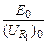. А это отношение велико, если падение напряжения происходит в основном на индуктивном сопротивлении: 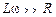. Поэтому, как отмечалось выше, если проводить измерения при достаточно больших частотах 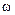, можно получить хорошую точность, используя упрощенную формулу (15.12).

Задание к работе

1. Подключите последовательно соединенные резистор 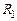и катушку индуктивности 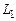без ферромагнитного сердечника к генератору прямоугольных импульсов (рис. 15.3).

2. Подключите Y-вход осциллографа к резистору 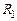. На генераторе установите частоту 1200 Гц. Получите на экране устойчивую картину изменения напряжения на этом сопротивлении со временем, подобную изображенной на рис. 15.1. Зная время развертки осциллографа, определите время релаксации 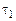(см. Приложение).

3. Отключите сопротивление 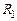и замените его сопротивлением .

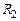4. Определите с помощью осциллографа время релаксации .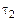

5. Пользуясь формулами (15.16) и (15.17), определите величины
R^* и L₁.

6. Приступите к измерению индуктивности вторым способом. Для этого подключите последовательно соединенные резистор 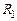и катушку индуктивности 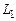к звуковому генератору (рис. 15.4), установив на нем значение частоты ~15 кГц и некоторое значение амплитуды сигнала.

7. С помощью осциллографа измерьте амплитудное значение падения напряжения на резисторе .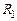

8. Повторите измерения амплитуды при частотах ~6 и ~2 кГц.

9. Отключите осциллограф от концов резистора, а звуковой генератор от RL-контура и, не изменяя величину его сигнала, измерьте с помощью осциллографа амплитудное значение ЭДС генератора .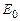

11. Вычислите индуктивность по формуле (15.12) для всех трех частот.

12. Сравните результаты измерения, объясните различия.

Контрольные вопросы

1. В чем состоит явление электромагнитной индукции?

2. Сформулируйте закон Фарадея и правило Ленца для электромагнитной индукции.

3. Объясните физическую причину появления индукционного тока в неподвижном контуре, помещенном в переменное магнитное поле.

4. Найдите выражение для ЭДС индукции и индукционного тока в плоском витке, равномерно вращающемся в однородном, стационарном магнитном поле.

5. В чем состоит явление самоиндукции? Напишите выражение для ЭДС самоиндукции.

6. Что называется индуктивностью контура? От чего она зависит?

7. Как определить индуктивность контура путем подключения и отключения внешнего источника ЭДС (т.е. первым способом)?

8. Объясните физический смысл времени релаксации. Как, измерив это время, определить индуктивность соленоида?

9. Как повысить точность этих измерений? Получите соответствующие рабочие формулы.

10. Как, используя вынужденные электромагнитные колебания, осуществить измерение индуктивности соленоида вторым способом? Получите соответствующую формулу.

11. Что влияет на точность измерения индуктивности вторым способом и как её повысить?

Список литературы

1. Яворский Б.М., Детлаф А.А., Милковская Л.Б. Курс физики: Учебник. – М.: Высш. шк., 1964. – Т. 2: Электричество и магнетизм.

2. Савельев И.В. Курс общей физики. – М.: Наука, 1978. – Т. 2
(и последующие издания этого курса).

Лабораторная работа № 16