Дифференциальные уравнения движения идеальной жидкости
В потоке идеальной жидкости возьмем точку M с координатами x, y, z и выделим возле нее элемент жидкости в форме прямоугольного параллелепипеда так, чтобы точка M была одной из его вершин (Рис. 20). Ребра параллелепипеда параллельны координатным осям и равны dx, dy, dz. Составим уравнение движения этого элемента жидкости. Пусть на жидкость внутри него действует результирующая единичная массовая сила с составляющими X, Y и Z. Тогда массовые силы, действующие на выделенный объем будут равны этим составляющим, умноженным на массу элемента. Поверхностные силы будут равны давлениям, умноженным на площади граней параллелепипеда.
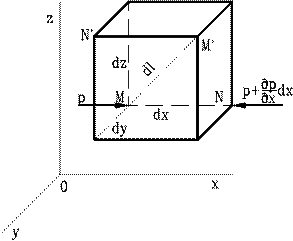
Рис. 20. Схема для вывода дифференциальных уравнений движения
идеальной жидкости.
Согласно второму закону Ньютона, уравнения движения вдоль координатных осей примут вид:
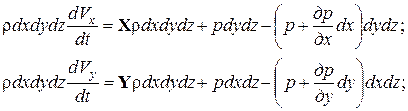
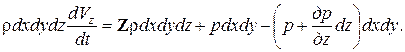
Приведя подобные и разделив уравнения на массу элемента rdxdydz, получим
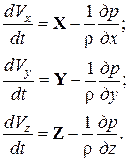
Эта система дифференциальных уравнений движения идеальной жидкости носит название уравнений Эйлера. Все члены этих уравнений имеют размерность ускорений, а смысл каждого уравнения состоит в следующем: полное ускорение частицы вдоль координатной оси складывается из ускорения от массовых сил и ускорения от сил давления.
Эти уравнения справедливы как для несжимаемой, так и для сжимаемой жидкости, как для стационарного, так и нестационарного течения.
Для стационарного течения умножим каждое из уравнений на соответствующие проекции элементарного перемещения, равные dx = Vxdt; dy = Vydt; dz = Vzdt, и сложим уравнения. Получим
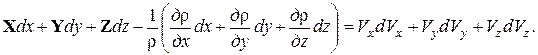
Выражение в скобках – это полный дифференциал давления dp, выражения в правых частях – дифференциалы от половин квадратов проекций скорости:
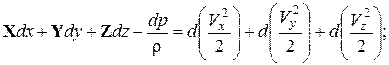
или
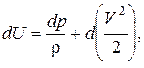
где U – силовая функция.
Рассмотрим частный случай этого уравнения, когда из массовых сил действует только сила тяжести: X = Y = 0; Z = – g. Подставляя эти значения, получим:
,
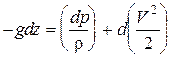или
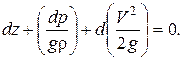
Для идеальной жидкости плотность r = const, так как эта жидкость абсолютно несжимаемая. Поэтому предыдущее уравнение можно переписать в виде
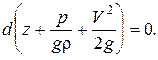
Следовательно,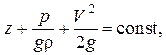 
то есть мы получили уравнение Бернулли для элементарной струйки идеальной жидкости.
Уравнение Бернулли для элементарной струйки идеальной жидкости
Рассмотрим установившееся течение идеальной жидкости, находящейся под действием только одной массовой силы – силы тяжести. Возьмем одну из элементарных струек потока и выделим сечениями 1 и 2 участок струйки произвольной длины. Пусть площади сечений равны dS1 и dS2, скорости в них V1 иV2, давления – p1 и p2, а высоты от произвольного уровня z1 и z2.
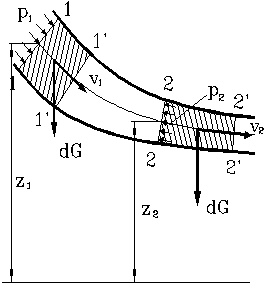
Рис. 18. Схема для вывода
уравнения Бернулли
За бесконечно малый отрезок времени dt участок струйки сместится в положение 1’ – 2’.
Из механики известно, что работа сил, приложенных к телу, равна приращению кинетической энергии тела. В данном случае к участку струйки приложены поверхностные силы давления и массовая сила – сила тяжести.
Работа сил давления в первом сечении положительна, так как направление силы совпадает с направлением перемещения, во втором – отрицательная, а на боковой поверхности струйки равна нулю (вектора силы и скорости перпендикулярны).
Работа сил давления в первом сечении положительна, так как направление силы совпадает с направлением перемещения, во втором – отрицательная, а на боковой поверхности струйки равна нулю (вектора силы и скорости перпендикулярны).
Работа равна произведению силы на перемещение вдоль направления силы. Тогда работа сил давления будет равна
p1 dS1 V1 dt – p2 dS2 V2 dt.
Работа силы тяжести равна изменению потенциальной энергии положения участка струйки, поэтому надо из энергии положения жидкости в объеме 1 – 2 вычесть энергию положения в объеме 1’ – 2’. При этом энергия положения объема 1’ – 2 остается неизменной, и останется лишь разность энергий элементов 1 – 1’ и 2 – 2’. Учитывая уравнение расхода, просто заметить, что вес обоих элементов одинаков
dG = gr V1 dt dS1= gr V2 dt dS2.
Тогда работа силы тяжести: dG(z1 – z2).
При вычислении приращения кинетической энергии рассматриваемого участка струйки за время dt, необходимо из кинетической энергии объема 1’ – 2’ вычесть кинетическую энергию объема 1 – 2. Получится разность кинетических энергий объемов 2 – 2’ и 1 – 1’. Таким образом, приращение кинетической энергии участка струйки равно
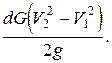
Из полученных выражений составим уравнение:
p1 dS1 v1 dt – p2 dS2 v2 dt+ dG(z1 – z2) =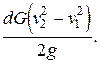 
Разделим его на dG
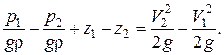
Перегруппировав слагаемые, получим уравнение Бернулли для элементарной струйки идеальной жидкости:
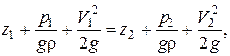
где z – геометрический напор (высота);
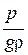– пьезометрический напор (высота);
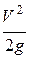– скоростной напор (высота).
Так как сечения струйки взяты произвольным образом, то сумма этих трех напоров (H – полный напор) есть величина постоянная вдоль струйки:
H =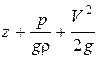 
= const.
Уравнение Бернулли можно переписать через удельные энергии. Для этого домножим его на g:
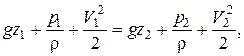
где gz – удельная энергия положения;
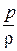– удельная энергия давления движущейся жидкости;
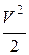– удельная кинетическая энергия.
Мы видим, что последнее уравнение – это уравнение закона сохранения механической энергии.
Если это уравнение домножить еще и на r, то получим уравнение Бернулли, записанное через давления:
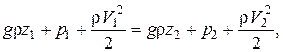
где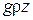 
– весовое давление;
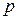– гидромеханическое давление;
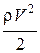– динамическое давление.
Проиллюстрируем уравнение Бернулли графиком (Рис. 19), на котором показано изменение всех трех напоров вдоль элементарной струйки. Линия изменения пьезометрических напоров называется пьезометрической линией. Ее можно рассматривать как геометрическое место уровней в пьезометрах, установленных вдоль струйки.
Из графика хорошо видно, что изменение площади живого сечения струйки приводит к заметному изменению скоростного напора. При уменьшении диаметра живого сечения в 2 раза скорость возрастает также в 2 раза, а скоростной напор – в 4 раза. При горизонтальном расположении струйки это изменение происходит за счет изменения пьезометрического напора. При резком сужении элементарной струйки пьезометрический напор, а значит и давление, могут упасть настолько, что последнее станет меньше атмосферного, то есть возникнет разрежение.
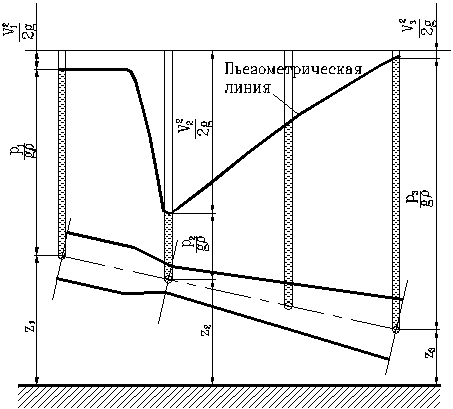
Рис. 19. Изменение напоров вдоль струйки идеальной жидкости
На первый взгляд, согласно уравнения Бернулли, при очень сильном сужении струйки абсолютное давление может стать и вовсе отрицательным, что в принципе невозможно. Дело в том, что при снижении давления в струйке до давления насыщенных паров жидкость начнет резко испаряться, и давление останется положительным. Но в этом случае пользоваться уравнением Бернулли уже нельзя, так как при его выводе использовалось уравнение расхода, которое справедливо только при условии, что не нарушается сплошность среды.
Использование уравнения Бернулли в технике
Рассмотрим некоторые технические устройства, использующие в своей работе уравнение Бернулли.
Расходомер Вентури (Рис. 23) – это устройство, устанавливаемое в трубопроводе и осуществляющее сужение (дросселирование) потока жидкости.
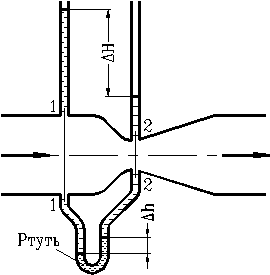
Рис. 23. Схема расходомера
Вентури
Расходомер состоит из двух участков – плавно сужающегося (сопла) и постепенно расширяющегося (диффузора). В узком месте потока скорость его возрастает, а давление падает. Возникает перепад давлений, который может фиксироваться либо двумя пьезометрами, либо дифференциальным U-образным манометром и связан с расходом. Установим эту связь. Будем считать, что распределение скоростей в сечениях трубопровода равномерное, тогда коэффициент Кориолиса a =1.
Запишем уравнения Бернулли и расхода для двух сечений, указанных на схеме:
.
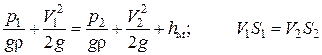Дополним эту систему уравнений еще двумя:
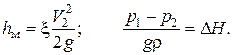
Выразим из уравнения расхода скорость V1 и подставим ее и два последних выражения в уравнение Бернулли:
.
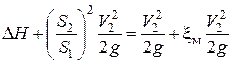Найдем из этого выражения V2:
.
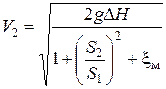Отсюда объемный расход
,
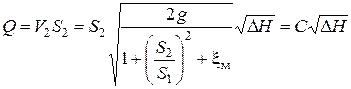где C – величина, постоянная для данного расходомера, которую, чаще всего, определяют опытным путем.
Зная C, можно по показаниям пьезометров определить расход в любой трубе, в которую будет установлен данный расходомер.
Если вместо пьезометров подключен U-образный дифференциальный манометр, заполненный ртутью, то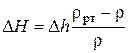 
.
Трубка полного напора (трубка Пито) (Рис. 24) служит для измерения скорости, например в трубе.
В пьезометре, конец которого загнут навстречу потоку жидкость поднимется выше, чем обычном пьезометре на величину скоростного напора. Это объясняется тем, что жидкость попавшая в этот пьезометр полностью останавливается, поэтому при a =1 можно записать уравнение Бернулли для невозмущенного потока и сечения, в котором расположены пьезометры:
.
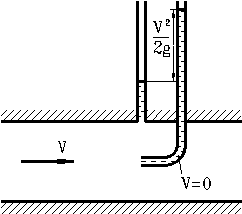
Рис. 24. Схема трубки полного напора
Отсюда
,
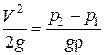тогда
.
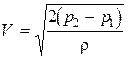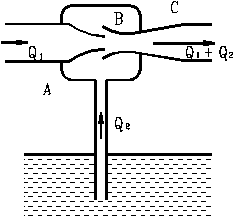
Рис. 25. Схема струйного насоса
Струйный насос (эжектор) (Рис. 25) состоит из плавно сходящегося насадка А, осуществляющего сжатие потока, и постепенно расширяющейся трубки С, установленной на некотором расстоянии от насадка в камере B.
Вследствие сужения потока в насадке A возрастает скорость потока, а давление в нем и во всей камере В снижается. В трубке С скорость потока постепенно снижается, а давление возрастает приблизительно до атмосферного. Следовательно, в камере В возникает разрежение, под действием которого жидкость из нижнего резервуара всасывается в камеру В, где происходит слияние и перемешивание двух потоков.
Чаще всего, первый поток – это поток воздуха, а второй – жидкость, которую необходимо распылять.