Порядок выполнения работы. 1. С помощью соединительных проводов подключить источник питания к электродам

1. С помощью соединительных проводов подключить источник питания к электродам.

2. К этим же электродам подсоединить вольтметр (предел 0¸20В, постоянный ток) и выставить напряжение 3¸5В.

3. Одним из щупов вольтметра произвести измерения потенциала во всех точках панели (если точек много, то измерять через одну и по вертикали и по горизонтали).

Задание № 1

1. Нанести полученные результаты на бумагу и соединить плавными линиями точки, в которых значения потенциала совпадают.

2. Построить линии напряженности.

Задание № 2

1. По формуле (1.34) найти значение напряженности результирующего поля в точке указанной преподавателем (не менее 2 ^{– х} раз).

2. Оцените погрешность данного измерения.

Контрольные вопросы

1. Электростатическое поле, условие возникновения, силовые линии, эквипотенциальные поверхности.

2. Заряд, закон сохранения заряда, закон Кулона, диполь.

3. Силовая характеристика электрического поля (определение, размерность).

4. Вывод Е поля плоскости, 2 ^{- х} плоскостей.

5. Вывод Е поля бесконечной заряженной нити.

6. Работа в электростатическом поле.

7. Энергетическая характеристика электрического поля.

8. Связь между силовой и энергетической характеристиками поля.

9.Доказать, что линии напряженности электростатического поля перпендикулярны эквипотенциальным поверхностям.

Литература

1. Детлаф А.А., Яворский Б.М. Курс физики, М.: Высшая школа. 1989. Том II. Глава 13 и 14.

2. Зисман Г.А., Тодес О.М. Курс общей физики, М.: Наука. 1972. Том 2, глава 1 и 2.

3. Сорокин А.Ф., Сурков М.И., Кушкин С.А. Руководство к лабораторным работам по физике. Астрахань 1997г.

Лабораторная работа № 2.

Измерение неизвестных емкостей при помощи баллистического гальванометра.

Цель работы: измерение емкостей конденсаторов баллистическим методом измерения неизвестных емкостей.

Оборудование: набор конденсаторов (С), гальванометр, источник питания 0÷7 V, соединительные провода.

Краткая теория

Рассмотрим два проводника, между которыми существует электрическое напряжение, предположим, что все линии напряженности, исходящие из одного проводника, заканчиваются на другом. Такую пару проводников мы будем называть простым конденсатором или просто конденсатором. Конденсатором называется устройство, способное накапливать энергию электрического поля.

Простым конденсатором является шаровой конденсатор, состоящий из двух проводников в виде концентрических сфер, так как линии напряженности, исходящие из внутренней сферы, обязательно все заканчиваются на внешней сфере. Две параллельные проводящие пластины (плоский конденсатор) можно считать также простым конденсатором, если расстояние между пластинами мало по сравнению с их размерами. Простым конденсатором является и цилиндрический конденсатор, если длина цилиндров велика по сравнению с зазором между ними. Оба проводника, образующие конденсатор, называются его обкладками.

Так как линии смещения начинаются и заканчиваются на электрических зарядах, отсюда следует, что заряды, находящиеся на обкладках простого конденсатора, всегда равны по модулю и противоположны по знаку.

Напряженность поля в любой точке между обкладками конденсатора всегда пропорциональна заряду обкладок. Поэтому и напряжение U между обкладками всегда пропорционально заряду обкладок q.

q=C×U. (2.1)

Коэффициент С в этой формуле называют электрической емкостью конденсатора или просто его емкостью. Единицей емкости служит фарад (Ф)- емкость такого уединенного проводника, потенциал которого повышается на 1В при сообщении заряда 1 Кл. Это очень большая единица измерения. Емкости используемых в практике конденсаторов обычно указываются в мкФ (10^-6 Ф) или в пФ (10^-12 Ф). Емкость конденсатора является его основной характеристикой и зависит от его размеров, формы и от свойств среды, находящейся между его обкладками.

Пусть С₀ – емкость любого конденсатора, когда его обкладки находятся в вакууме. Практически мы получим ту же емкость, если между обкладками будет атмосферный воздух. Пусть далее С- емкость того же конденсатора, если все пространство между его обкладками заполнено каким-либо другим однородным диэлектриком. Отношение

C/C₀=e

называют относительной диэлектрической проницаемостью или просто диэлектрической проницаемостью диэлектрика.

Емкость конденсаторов простой формы можно вычислить. Для этого предполагают, что на каждой из обкладок находится некоторый заряд q, и вычисляют потенциал в электрическом поле рассматриваемого конденсатора U (x,y,z). Если удается решить эту задачу, то отсюда получается и значение напряжения между обкладками конденсатора U. После этого емкость можно найти по формуле (2.1)

Рассмотрим некоторые примеры.

Пример 1. Плоский конденсатор. Плоский конденсатор состоит из двух параллельных металлических пластин площадью S каждая, расположенных на близком расстоянии d одна от другой. Заряды пластин +q и –q.Если линейные размеры пластин велики по сравнению с d, то электростатическое поле между пластинами можно считать таким же, как поле между двумя плоскостями, заряженными разноименно с поверхностными плотностями зарядов s = q/S ,(+σ и -s). Направим ось перпендикулярно плоскости. Напряженность поля конденсатора между пластинами

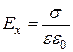(0£ x£ d),

где e -относительная диэлектрическая проницаемость среды, заполняющей конденсатор. Из связи

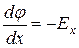
получаем, что

,

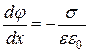тогда разность потенциалов равна