Контрольная работа № 5

Вариант	Номера задач

Задачи

1. На мыльную пленку (n=1,3), находящуюся в воздухе, падает нормально пучок лучей белого света. При какой наименьшей толщине d пленки отраженный свет с длиной волны λ=0,55 мкм окажется максимально усиленным в результате интерференции?

2. На тонкий стеклянный клин (n=1,55) падает нормально монохроматический свет. Двугранный угол между поверхностями клина составляет α=2^/. Определить длину световой волны, если расстояние между смежными интерференционными максимумами в отраженном свете b=0,3 мм.

3. Поверхности стеклянного клина образуют между собой угол 0,2^/. На клин нормально к его поверхности падает пучок лучей монохроматического света с длиной волны λ=0,55 мкм. Определить ширину интерференционной полосы.

4. Плосковыпуклая линза (n=1,6) выпуклой стороной прижата к стеклянной пластинке. Расстояние между первыми двумя кольцами Ньютона, наблюдаемыми в отраженном свете, равно 0,5 мм. Определить оптическую силу линзы, если освещение производится монохроматическим светом с λ=0,55 мкм, падающим нормально.

5. Две плосковыпуклые линзы с радиусами R₁ и R₂ сложены выпуклыми поверхностями. Радиус m-го светлого интерференционного кольца, наблюдаемого в отраженном свете, равен r_m для длины волны λ. Определить радиус r_m, если R₁=1,4 м; R₂=2,7 м; λ=0,59 мкм; m=11.

6. Кольца Ньютона в отраженном свете наблюдаются с помощью плосковыпуклой линзы с радиусом кривизны R₁, положенной на вогнутую сферическую поверхность с радиусом кривизны R₂. Длина волны света равна λ, радиус m-го темного кольца r_m. Определить радиус r_m, если R₁=1,1 м; R₂=3,2 м; λ=0,55 мкм; m=5.

7. Кольца Ньютона в отраженном свете наблюдаются с помощью плосковыпуклой линзы с радиусом кривизны R₁, положенной на вогнутую сферическую поверхность с радиусом кривизны R₂. Длина волны света равна λ, радиус m-го темного кольца r_m. Определить радиус r_m, если R₁=1,4 м; R₂=2,3 м; λ=0,59 мкм; m=12.

8. Плоская волна падает на круглый диск радиуса r. Точка наблюдения находится на расстоянии b от диска. Ширина зоны Френеля, непосредственно примыкающей к диску, равна x при длине волны λ. Определить радиус r, если b=2,4 м; x=0,95 мм; λ=0,63 мкм.

9. Плоская волна падает на круглый диск радиуса r. Точка наблюдения находится на расстоянии b от диска. Ширина зоны Френеля, непосредственно примыкающей к диску, равна x при длине волны λ. Определить ширину зоны x, если b=1,7 м; r=3,5 мм; λ=0,55 мкм.

10. Плоская волна падает на круглый диск радиуса r. Точка наблюдения находится на расстоянии b от диска. Ширина зоны Френеля, непосредственно примыкающей к диску, равна x при длине волны λ. Определить расстояние b, если x=1,3 мм; r=2,2 мм; λ=0,59 мкм.

11. На диафрагму с круглым отверстием радиусом r=1 мм падает нормально параллельный пучок света с длиной волны 0,5 мкм. На пути лучей, прошедших через отверстие, помещают экран. Определить максимальное расстояние b_max от центра отверстия до экрана, при котором в центре дифракционной картины еще будет наблюдаться темное пятно.

12. Радиус четвертой зоны Френеля для плоского волнового фронта равен 3 мм. Определить радиус шестой зоны Френеля.

13. Плоская световая волна (λ=0,5 мкм) падает нормально на диафрагму с круглым отверстием диаметром d=1 см. На каком расстоянии b от отверстия должна находиться точка наблюдения, чтобы отверстие открывало: 1) одну зону Френеля? 2) Две зоны Френеля?

14. На щель шириной, а=0,05 мм падает нормально монохроматический свет (λ=0,6 мкм). Определить угол между первоначальным направлением пучка света и направлением на четвертую темную дифракционную полоску.

15. Вследствие изменения температуры абсолютно черного тела максимум спектральной плотности энергетической светимости сместился с 24000 Å на 8000 Å. Как и во сколько раз изменились энергетическая светимость тела и максимальное значение спектральной плотности энергетической светимости?

16. Температура абсолютно черного тела равна 2000 К. Определить: 1) спектральную плотность энергетической светимости для длины волны λ=6000 Å; 2) энергетическую светимость в интервале длин волн от 5900 Å до 6100 Å. Принять, что среднее значение спектральной плотности энергетической светимости тела в этом интервале равно значению, найденному для длины волны 6000 Å.

17. Энергия, излучаемая через смотровое окошко печи за время t=5 с, равна W. Площадь окошка равна S=5,5 см², максимум в спектре излучения приходится на длину волны λ=1,6 мкм. Определить энергию W.

18. Модель абсолютно черного тела – полость с малым круглым отверстием диаметром d=1,5 см. Нагрев производится электрической спиралью, потребляющей ток I=35 мА при напряжении U=220 В, причем некоторая доля энергии р рассеивается стенками полости. Равновесная температура излучения, исходящего из отверстия, равна Т=870 К. Определить энергию р.

19. Какое количество энергии излучает в течении суток каменное оштукатуренное здание общей поверхностью 1000 м², если коэффициент поглощения (поглощательная способность) при этом 0,8 и температура излучающей поверхности 0^°С.

20. Стальная болванка, температура которой 727^°С, излучает за 1с 4 Дж энергии с поверхности 1 см². Определить коэффициент поглощения (поглощательную способность) болванки при данной температуре, считая, что он одинаков для всех волн.

21. 1) Найти насколько уменьшится масса Солнца за год вследствие излучения? 2) Считая излучение Солнца постоянным, найти за какое время масса Солнца уменьшится вдвое. Температуру поверхности Солнца принять равной 5800 К.

22. Поверхность тела нагрета до температуры 1000 К. Затем одна половина этой поверхности нагревается на 100 К, а другая охлаждается на 100 К. Во сколько раз изменится энергетическая светимость поверхности этого тела?

23. Температура абсолютно черного тела изменилась при нагревании от 1000 К до 3000 К. 1) Во сколько раз увеличилась при этом его энергетическая светимость? 2) Насколько изменилась при этом длина волны, на которую приходится максимум спектральной плотности энергетической светимости?

3) Во сколько раз увеличилась его максимальная спектральная плотность энергетической светимости?

24. Поток монохроматического излучения (λ=500 нм) падает нормально на плоскую зеркальную поверхность и давит на нее с силой 10^-8 Н. Определить число фотонов, ежесекундно падающих на эту поверхность.

25. Параллельный пучок монохроматических лучей (λ=662 нм) падает на зачерненную поверхность и производит на нее давление 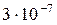Н/м². Определить концентрацию фотонов в световом пучке.

26. Длина волны λ фотона равна комптоновской длине волны электрона. Определить энергию Е и импульс фотона р.

27. Во сколько раз энергия фотона (λ=550 нм) больше средней кинетической энергии поступательного движения молекулы кислорода при комнатной температуре Т=20 ^°С?

28. Определить поверхностную плотность потока энергии излучения I, падающего на зеркальную поверхность, если световое давление при перпендикулярном падении лучей равно р=10 мкПа.

29. Поток энергии, излучаемый электрической лампой, равен Ф_е=600 Вт. На расстоянии r=1 м от лампы перпендикулярно падающим лучам расположено круглое плоское зеркальце диаметром d=2 см. Принимая, что излучение лампы одинаково во всех направлениях и что зеркальце полностью отражает падающий на него свет, определить силу светового давления F на зеркальце.

30. На зеркальце с идеально отражающей поверхностью площадью S=1,5 см² падает нормально свет от электрической дуги. Определить импульс р, полученный зеркальцем, если поверхностная плотность потока излучения, падающего на зеркальцеравна I=0,1 МВт/м². Продолжительность облучения t=1 c.

31. Определить энергию Е и импульс р фотона, которому соответствует длина волны λ=380 нм (фиолетовая граница видимого спектра).

32. Определить длину волны λ и импульс р фотона с энергией Е=1 МэВ.

33. Давление монохроматического света (λ=600 нм) на черную поверхность, расположенную перпендикулярно падающим лучам, равно р=0,1 мкПа. Определить число фотонов N, падающих за время t=1 c на поверхность площадью S=1 см².

34. Монохроматическое излучение с длиной волны λ=500 нм падает нормально на плоскую зеркальную поверхность и давит на нее с силой F=10 нН. Определить число фотонов N, ежесекундно падающих на эту поверхность.

35. Определить давление солнечных лучей нормально падающих на зеркальную поверхность. Интенсивность солнечного излучения принять равной 1,37 кВт/м².

36. Плотность потока энергии в импульсе излучения лазера может достигать значения 1,3∙10²⁰ Вт/м². Определить давление такого излучения, нормально падающего на черную поверхность.

37. Свет с длиной волны λ=500 нм нормально падает на зеркальную поверхность и производит на нее давление р=4 мкПа. Определить число фотонов, ежесекундно падающих на 1 см² этой поверхности.

38. На платиновую пластинку падают ультрафиолетовые лучи. Для прекращения фотоэффекта нужно приложить задерживающую разность потенциалов 3,7 В. Если платиновую пластинку заменить пластинкой из другого металла, то задерживающую разность потенциалов нужно увеличить до 6 В. Определить работу выхода электронов с поверхности этой пластинки.

39. На цинковую пластинку падает монохроматический свет длиной волны λ=2200 Å. Определить максимальную скорость фотоэлектронов.

40. Красная граница фотоэффекта для металла с работой выхода А соответствует длине волны λ₀. При освещении поверхности металла излучением длиной волны λ=0,14 мкм максимальная скорость фотоэлектронов равна υ=1300 км/с. Определить работу выхода А.

41. При поочередном освещении поверхности некоторого металла светом с длинами волн λ₁=0,35 мкм и λ₂=0,54 мкм обнаружили, что соответствующие максимальные скорости фотоэлектронов отличаются друг от друга в n=2 раза. Найти работу выхода с поверхности этого металла.

42. Красная граница фотоэффекта рубидия 810 нм. Какую обратную разность потенциалов нужно приложить к фотоэлементу, чтобы задержать электроны, испускаемые рубидием под действием ультрафиолетовых лучей длиной волны 100 нм?

43. При падении излучения с длиной волны λ на пластинку из металла с красной границей фотоэффекта λ₁=0,35 мкм, задерживающее напряжение для фотоэлектронов равно U₁=1,4 В, а при падении на пластинку с красной границей λ₂=0,45 мкм оно равно U₂. Определить U₂.

44. Определить импульс электрона отдачи при эффекте Комптона, если фотон с энергией, равной энергии покоя электрона, был рассеян на угол равный 180^°.

45. Фотон с энергией 0,25 МэВ рассеялся на свободном электроне. Энергия рассеянного электрона 0,2 МэВ. Определить угол рассеяния.

46. Фотон с энергией 1 МэВ рассеялся на свободном покоившемся электроне. Найти кинетическую энергию электрона отдачи, если в результате рассеяния длина волны фотона изменилась на 25%.

47. Рентгеновский фотон испытал комптоновское рассеяние на угол θ=48^°. Первоначальная энергия фотона W₁=0, 15 МэВ, энергия электрона отдачи W_е. Найти энергию фотона после рассеяния W₂.

48. При рассеянии рентгеновского излучения с длиной волны λ=3,5 пм на угол θ кинетическая энергия отдачи равна W_е, угол между падающим фотоном и направлением движения электрона отдачи равен γ=22^°.

49. При рассеянии рентгеновского излучения с длиной волны λ на угол θ=130^° кинетическая энергия отдачи равна W_е=85 кэВ, угол между падающим фотоном и направлением движения электрона отдачи равен γ. Найти λ.

50. Определить наименьшее и наибольшее значения энергии фотона в ультрафиолетовой серии спектра водорода (серии Лаймана).

51. Фотон с энергией 16,5 эВ выбил электрон из невозбужденного атома водорода. Какую скорость будет иметь электрон вдали от ядра атома?

52. Электрон движется по второй орбите атома водорода. Найти длину волны де Бройля.

53. Атомарный водород переведен из нормального состояния в возбужденное, характеризуемое главным квантовым числом 3. Какие спектральные линии могут появиться в спектре водорода при переходе атома из возбужденного состояния в нормальное?

54. Атом водорода в основном состоянии поглотил квант света с энергией 12,09 эВ. Определить кинетическую, потенциальную и полную энергию электрона в возбужденном атоме?

55. Насколько изменится орбитальный момент импульса электрона в атоме водорода (момент количества движения) при испускании атомом второй по порядку спектральной линии серии Бальмера (электрон переходит с четвертого уровня на второй)?

56. Определить потенциальную, кинетическую и полную энергии электрона, находящегося на первой орбите атома водорода.

57. Найти наибольшую λ_max и наименьшую λ_min длины волн в первой инфракрасной серии спектра водорода (серии Пашена).

58. Найти энергию Е_i и потенциал U_i ионизации ионов He⁺и Li⁺⁺.

59. Вычислить частоты ν₁ и ν₂ вращения электрона в атоме водорода на второй и третьей орбитах. Сравнить эти частоты с частотой ν излучения при переходе электрона с третьей на вторую орбиту.

60. Атом водорода в основном состоянии поглотил квант света с длиной волны λ=121,5 нм. Определить радиус r электронной орбиты возбужденного атома водорода.

61. Определить первый потенциал U₁ возбуждения атома водорода.

62. Вычислить длину волны λ, которую испускает ион гелия He⁺ при переходе со второго энергетического уровня на первый. Сделать такой же подсчет для иона лития Li⁺⁺.

63. Оценить с помощью соотношения неопределенностей минимальную кинетическую энергию T_min электрона, движущегося внутри сферической области d=0,1 нм.

64. Атом испустил фотон с длиной волны λ=600 нм. Продолжительность излучения t=50 нс. Определить наибольшую точность (Δλ), с которой может быть измерена длина волны излучения.

65. Определить неточность Δx в определении координаты электрона, движущегося в атоме водорода со скоростью υ=1,5∙10⁶ м/с, если допускаемая неточность Δ υ в определении скорости составляет 10% от ее величины. Сравнить полученную неточность с диаметром d водорода, вычисленным по теории Бора для основного состояния, и указать, применимо ли понятие траектории в данном случае.

66. Электрон с кинетической энергией Т=15 эВ находится в металлической пылинке диаметром d=1 мкм. Оценить (в процентах) относительную неточность, с которой может быть определена скорость электрона.

67. Во сколько раз дебройлевская длина волны λ частицы меньше неопределенности ее координаты Δx, которая соответствует неопределенности ее импульса в 1%.

68. Используя соотношение неопределенностей 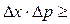ħ, оценить низший энергетический уровень электрона в атоме водорода. Принять линейные размеры атома 1 Å.

69. Ширина следа электрона от фотографии, полученной с помощью камеры Вильсона, составляет Δx=10^{-3 м}. Найти неопределенность в определении скорости.

70. За один год начальное количество радиоактивного изотопа уменьшилось в 3 раза. Во сколько раз оно уменьшится за два года.

71. За какое время t распадается ¼ начального количества ядер радиоактивного изотопа, если период его полураспада Т_1/2=24 часа?

72. За время t=8 суток распалось к=¾ начального количества ядер радиоактивного изотопа. Определить период полураспада.

73.Период полураспада радиоактивного нуклида Т_1/2=1 час. Определить среднюю продолжительность жизни τ этого нуклида.

74. Активность А препарата уменьшилась в к=250 раз. Скольким периодам полураспада Т_1/2 равен протекший промежуток времени t?

75. За время 1 сутки активность изотопа уменьшилась от А₁=118 ГБк до А₂=7,4 ГБк. Определить период полураспада Т_1/2 этого нуклида.

76. Определить промежуток времени τ, в течение которого активность А изотопа стронция Sr⁹⁰ уменьшится в к₁=10 раз? В к₂=100 раз?

77. Определить активность А фосфора Р³² массой m=1 мг.

78. Найти отношение массовой активности а₁ стронция Sr⁹⁰ к массовой активности а₂ радия Ra²²⁶.

79. Определить массу m₂ радона Rn²²², находящегося в радиоактивном равновесии с радием Ra²²⁶ массой m₂.

80. Уран U²³⁴ является продуктом распада наиболее распространенного изотопа урана U²³⁸. Определить период полураспада Т_1/2 U²³⁴, если его массовая доля ω в естественном уране U²³⁸ равна 6∙10^-5.

Статистическая физика