Электропроводность полупроводников
Рассмотрим примесный полупроводник, например, электронный. Энергетическая диаграмма его приведена на рис.2.

Рис.2. Энергетическая диаграмма электронного полупроводника (Т=0)
При абсолютном нуле электроны занимают уровни валентной зоны и примесные уровни. В зоне проводимости свободных электронов нет, сопротивление бесконечно велико, 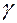 =0. По мере увеличения температуры начнётся переход с примесных уровней в зону проводимости. Концентрация электронов при этом растёт экспоненциально:
=0. По мере увеличения температуры начнётся переход с примесных уровней в зону проводимости. Концентрация электронов при этом растёт экспоненциально:
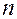 ~
~  , (11)
, (11)
где  - энергия активации примесной проводимости (в электронном полупроводнике она равна глубине залегания донорного уровня),
- энергия активации примесной проводимости (в электронном полупроводнике она равна глубине залегания донорного уровня),
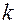 - постоянная Больцмана,
- постоянная Больцмана,
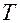 - абсолютная температура.
- абсолютная температура.
Формула (11) справедлива в области сравнительно низких температур, когда  . При дальнейшем увеличении температуры произойдёт «истощение» примесей, т.е. все электроны с примесных уровней переёдут в зону проводимости. Концентрация электронов при таких «средних» температурах (когда
. При дальнейшем увеличении температуры произойдёт «истощение» примесей, т.е. все электроны с примесных уровней переёдут в зону проводимости. Концентрация электронов при таких «средних» температурах (когда  ) постоянна и определяется концентрацией примеси (доноров):
) постоянна и определяется концентрацией примеси (доноров):  . При высоких температурах, когда
. При высоких температурах, когда  , начнётся переброс электронов из валентной зоны в зону проводимости. При этом в валентной зоне будут образовываться дырки, число дырок будет равно числу электронов. Концентрация носителей заряда увеличивается с температурой экспоненциально:
, начнётся переброс электронов из валентной зоны в зону проводимости. При этом в валентной зоне будут образовываться дырки, число дырок будет равно числу электронов. Концентрация носителей заряда увеличивается с температурой экспоненциально:
 ~
~  , (12)
, (12)
где  - ширина запрещённой зоны. При высоких температурах она будет являться энергией активации проводимости.
- ширина запрещённой зоны. При высоких температурах она будет являться энергией активации проводимости.
Температурная зависимость концентрации электронов представлена в координатах  на рис.3а:
на рис.3а:
 |  |
| а) | б) |
Рис.3. Температурная зависимость концентрации электронов (а) и удельной проводимости (б) электронного полупроводника.
1 – область низких температур,
2 – область средних температур,
3 – область высоких температур.
Подвижность электронов и дырок в полупроводниках на 2-3 порядка выше, чем в металлах (табл.1). Это связано с тем, вследствие малой концентрации свободных электронов в полупроводниках, электронный газ, как правило, не вырожден. Скорость хаотического движения электронов может быть определена по классической формуле  , она равна примерно 105 м/с. Согласно (8) в этом случае длина волны электрона будет около 7. Вследствие большей длины волны электронов неоднородности порядка атомных размеров мало влияют на рассеяние электронов. Хотя подвижность электронов в полупроводниках, как и в металлах, зависит от температуры, но по сравнению с изменением концентрации электронов изменение подвижности мало. Поэтому температурная зависимость удельной проводимости в основном определяется температурной зависимостью электронов. Влияние изменения подвижности заметно лишь в области средних температур (при «истощении» примеси). Температурная зависимость удельной проводимости в координатах
, она равна примерно 105 м/с. Согласно (8) в этом случае длина волны электрона будет около 7. Вследствие большей длины волны электронов неоднородности порядка атомных размеров мало влияют на рассеяние электронов. Хотя подвижность электронов в полупроводниках, как и в металлах, зависит от температуры, но по сравнению с изменением концентрации электронов изменение подвижности мало. Поэтому температурная зависимость удельной проводимости в основном определяется температурной зависимостью электронов. Влияние изменения подвижности заметно лишь в области средних температур (при «истощении» примеси). Температурная зависимость удельной проводимости в координатах  представлена на рис. 3б.
представлена на рис. 3б.
При низких температурах сопротивление полупроводника ( 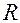 ~1/
~1/ 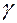 ) уменьшается с ростом температуры приблизительно экспоненциально:
) уменьшается с ростом температуры приблизительно экспоненциально:
 , (13)
, (13)
где  - константа, имеющая размерность сопротивления.
- константа, имеющая размерность сопротивления.
Энергию активации  можно найти, построив график зависимости
можно найти, построив график зависимости  . Прологарифмируем (13):
. Прологарифмируем (13):
 . (14)
. (14)

Рис.4. Определение энергии активации
График зависимости  представляет собой прямую линию, угловой коэффициент которой
представляет собой прямую линию, угловой коэффициент которой  (он равен тангенсу угла наклона
(он равен тангенсу угла наклона  ) пропорционален энергии активации:
) пропорционален энергии активации:
 (15)
(15)
Выбрав две (1 и 2) точки на прямой определяют:
 , (16)
, (16)
а затем энергию активации:
 (17)
(17)
