Где 1 и 2 обозначают начальное и конечное состояние системы
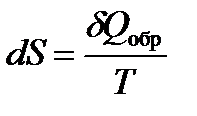
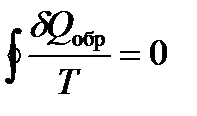 Строгий теоретический анализ показывает, что приведенное количество теплоты, сообщаемое телу в любом обратимом круговом процессе, равно нулю:
Строгий теоретический анализ показывает, что приведенное количество теплоты, сообщаемое телу в любом обратимом круговом процессе, равно нулю:
Из равенства нулю интеграла, взятого по замкнутому контору, следует, что подынтегральное выражение есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние.
Таким образом, энтропия является функцией состояния.
Приращение энтропии в изопроцессах.
Каждый из изопроцессов идеального газа характеризуется своим изменением энтропии, а именно:
1) Изохорический процесс: 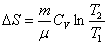 , т. к.
, т. к. 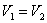
2) Изобарический процесс: 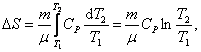 , т.к. Р1 = Р2;
, т.к. Р1 = Р2;
3) Изотермический процесс: 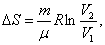 , т.к.
, т.к. 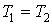
4) Адиабатический процесс: 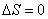 , т.к.
, т.к. 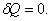
Отметим, что в последнем случае адиабатический процесс называют изоэнтропийным процессом, т.к. 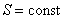 .
.
38.Статистический смысл ВНТ. Третье начало термодинамики.
Применение второго начала термодинамики (ВНТ) к изопроцессам.
Для решения задач и проведения расчетов удобно выразить изменение энтропии ΔS через параметры состояния.
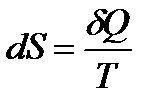 Изменение (приращение) энтропии находим из равенства Клаузиуса:
Изменение (приращение) энтропии находим из равенства Клаузиуса:
Дифференциальная форма выражения:
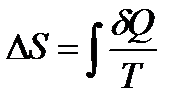
Интегральная форма выражения:
1. 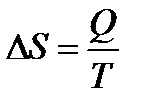 Изотермический процесс (Т=const, m=const)
Изотермический процесс (Т=const, m=const)
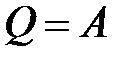
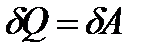 Так как Т=const, то изменение энтропии ΔS найдем из выражения:
Так как Т=const, то изменение энтропии ΔS найдем из выражения:
ПНТ для изотермического процесса имеет вид: или .
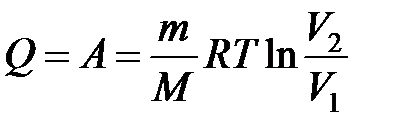 Работу при изотермическом процессе находим по формуле:
Работу при изотермическом процессе находим по формуле:
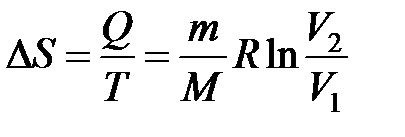 Подставляем в выражение для изменения энтропии, получаем:
Подставляем в выражение для изменения энтропии, получаем:
2. Изобарический процесс (p=const, m=const).
Изменение энтропии ΔS найдем из выражения:
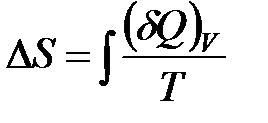
Количество теплоты подводимой к телу найдем по формуле:
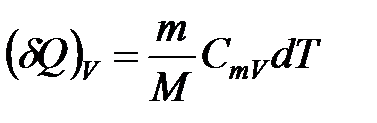
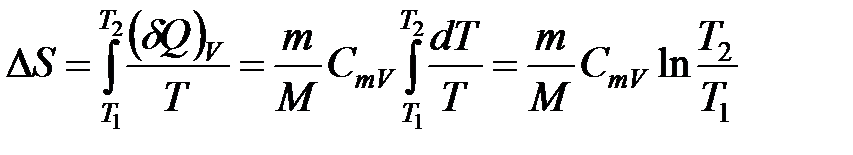 Подставляем эту формулу в выражение для изменения энтропии, получаем:
Подставляем эту формулу в выражение для изменения энтропии, получаем:
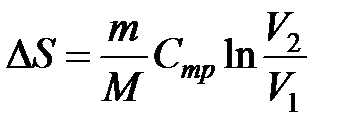 Полученная формула применима для расчета изменения энтропии не только для идеального газа (ИГ), но и для любых тел, молярная теплоемкость Сmp которых не зависит от температуры. Для ИГ она может быть также записана в виде:
Полученная формула применима для расчета изменения энтропии не только для идеального газа (ИГ), но и для любых тел, молярная теплоемкость Сmp которых не зависит от температуры. Для ИГ она может быть также записана в виде:
3. 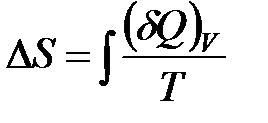 Изохорический процесс (V=const, m=const) .
Изохорический процесс (V=const, m=const) .
Изменение энтропии ΔS найдем из выражения:
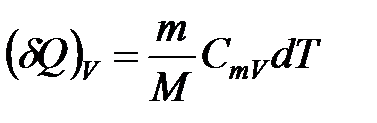 Количество теплоты подводимой к телу найдем по формуле:
Количество теплоты подводимой к телу найдем по формуле:
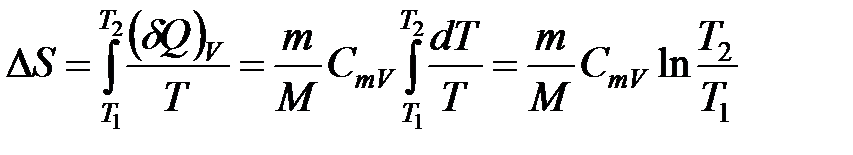 Подставляем эту формулу в выражение для изменения энтропии, получаем
Подставляем эту формулу в выражение для изменения энтропии, получаем
Адиабатический процесс.
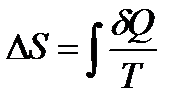 При адиабатическом процессе dQ = 0
При адиабатическом процессе dQ = 0
Подставим в выражение для изменение энтропии ΔS:
Получаем, DS = 0, отсюда следует, что S = const.
Адиабатический процесс является изоэнтропийным.
Поэтому адиабатический процесс обозначают символом S.
