С помощью магнетрона»
МЕТОДИЧЕСКОЕ УКАЗАНИЕ К ЛАБОРАТОРНОЙ РАБОТЕ № 2-М.
«ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА
С ПОМОЩЬЮ МАГНЕТРОНА».
| Составители: | А.И.Горковенко |
| И.Г. Фатеев |
Тюмень 2002г.
ЛАБОРАТОРНАЯ РАБОТА № 2
ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА
С ПОМОЩЬЮ МАГНЕТРОНА
| Цель работы: | экспериментальное определение удельного заряда электрона методом отклонения движущихся электронов в магнитном поле. |
| Оборудование: | электронная лампа, соленоид, два амперметра, вольтметр, два реостата, источник постоянного тока. |
ВВЕДЕНИЕ
Одной из главных характеристик заряженной частицы, как и всякого заряженного тела, является электрический заряд q. Однако движение заряженной частицы в электрическом и магнитном полях определяется не зарядом q, а отношением заряда q к массе частицы, называемым удельным зарядом.
Поясним это на некоторых примерах.
1. Пусть частица с зарядом q движется в электрическом поле напряженности Е. Сила F, действующая на частицу в поле равна
F=qE.
Запишем для такой части уравнение движения:
F=qE=ma.
Нетрудно видеть, что ускорение a=qE/m заряженной частицы в электрическом поле зависит от ее удельного зарядa
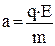 (1)
(1)
2. Пройдя разность потенциалов U, заряженная частица приобретает кинетическую энергию, равную величине
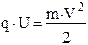
Из этого равенства следует, что скорость V частицы также определяется удельным зарядом
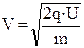
3. Если заряженная частица, движущаяся по инерции со скоростью 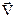 , попала в магнитное поле, то на нее со стороны поля действует сила Лоренца
, попала в магнитное поле, то на нее со стороны поля действует сила Лоренца
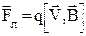
В соответствии с правилами векторного умножения направление силы 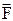 перпендикулярно как скорости
перпендикулярно как скорости 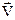 , так и вектору магнитной индукции
, так и вектору магнитной индукции 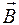 (см. рис.1). Следовательно, элементарная работа dA по перемещению заряда q в магнитном поле с индукцией В равна
(см. рис.1). Следовательно, элементарная работа dA по перемещению заряда q в магнитном поле с индукцией В равна 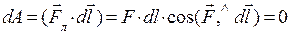 , т.е. значение кинетической энергии
, т.е. значение кинетической энергии 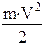 частицы в магнитном поле сохраняется, сохраняется численное значение (модуль) скорости
частицы в магнитном поле сохраняется, сохраняется численное значение (модуль) скорости 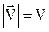 . Изменяется лишь направление скорости, а это означает, что заряженная частица однородном магнитном поле должна двигаться точно по окружности, если нет составляющей скорости вдоль магнитного поля.
. Изменяется лишь направление скорости, а это означает, что заряженная частица однородном магнитном поле должна двигаться точно по окружности, если нет составляющей скорости вдоль магнитного поля.
Таким образом, сила Лоренца выступает в качестве центростремительной силы (см. рис.1 и 2).
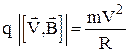 (3)
(3)
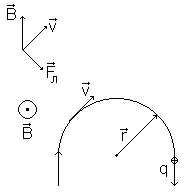 | 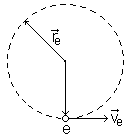 |
| Рис.1. | Рис.2. |
Траектория движения положительно заряженной частицы, в однородном поле  . /Поле направлено к нам./ . /Поле направлено к нам./ | Траектория движения электрона в однородном магнитном поле. |
Из выражения (3) можно найти радиус траектории
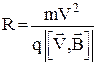
Таким образом, масштаб движения заряженной частицы в магнитном поле определяется также значением удельного заряда частицы q/m.
Рассмотренные примеры показывают, что разные частицы, но с одинаковым удельным зарядом, будут двигаться в электрическом и магнитном полях совершенно одинаково. Этим и определяется важное значение величины удельного заряда.
В истории физики опытное определение удельного заряда сыграло очень важную роль, т.к. оно предшествовало определению заряда и массы частиц и сделало возможным это определение. Дело в том, что ни уравнение (2), относящееся к движению частиц в электрическом поле, ни уравнение (3), описывающее движение частиц в магнитном поле, не позволяют определить заряд и массу частицы порознь, т.к. в каждом из этих уравнений содержится три неизвестные величины V, q и m. По той же причине заряд и масса не могут быть определены и при совместном решении обоих уравнений. Но если определять не qи m в отдельности, а их отношение, т.е. удельный заряд, то оба уравнения содержат лишь два неизвестных 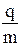 и V и поэтому их совместное решение возможно. На этом и основано большинство методов экспериментального определения удельного заряда частиц. Для этого исследуется движение частиц одновременно в электрическом и магнитном полях, так чтобы можно было использовать уравнения (2) и (3).
и V и поэтому их совместное решение возможно. На этом и основано большинство методов экспериментального определения удельного заряда частиц. Для этого исследуется движение частиц одновременно в электрическом и магнитном полях, так чтобы можно было использовать уравнения (2) и (3).
Непосредственно тем или иным способом могут быть определены разность потенциалов электрического поля, напряженность магнитного поля и радиус окружности, по которой частица движется в магнитном поле.
ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ
В настоящей работе отношение заряда электрона е к его массе m определяется при помощи метода получившего название «метода магнетрона». Это название связано с тем, что применяемая в работе конфигурация электрического и магнитного полей очень напоминает конфигурацию полей в магнетронах – генераторах электромагнитных колебаний в области сверхвысоких частот.
Движение электронов в этом случае происходит в кольцевом пространстве, заключенном между катодом и анодом двухэлектродной электронной лампы.
В качестве источника электронов используется подогреваемый нитью накала катод электронной лампы. Катод располагается вдоль оси цилиндрического анода так, что электрическое поле направленно от анода к катоду по радиусу.
Лампа помещается внутри соленоида, создающее магнитное поле параллельное катоду. Величина индукции В магнитного поля находится по формуле:
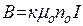 (4)
(4)
где 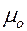 – магнитная постоянная, равная
– магнитная постоянная, равная 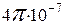 Гн/м;
Гн/м;
no - число витков, приходящихся на единицу длины соленоида;
I - сила тока, протекающего по виткам соленоида;
к – коэффициент, учитывающий конечные размеры соленоида, а также экранирующее влияние анода лампы (в нашем случае к=0,26).
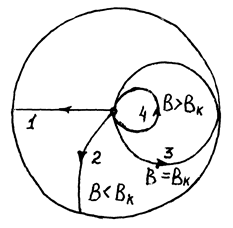 Рис.3 Траектория электронов, выле-тающих из катода при разных значениях индукции магнит-ного поля Рис.3 Траектория электронов, выле-тающих из катода при разных значениях индукции магнит-ного поля |
Рассмотрим траекторию движения электронов, вылетевших из катода при потенциале на аноде U. В отсутствие магнитного поля (В=0) траектория электронов представляет собой прямую линию (прямая 1 на рис.3). В слабом поле (В<Вк) траектория несколько искривляется, но электроны попадают на анод (кривая 2). При некотором значении поля В=Вк, называемым критическим, траектория движения электрона настолько искривляется, что коснется анода в точке А (кривая 3). Наконец при В>Вк электрон вовсе не попадет на анод и возвратится к катоду. В первом приближении можно считать, что электроны в пространстве между катодом и анодом движутся в магнитном поле В=Вк по окружности, радиус которой r равен половине радиуса анода лампы RA (r=RA/2). Радиус катода мал по сравнению с радиусом анода. С учетом сказанного, решая совместно уравнения (2), (3) и (4), получим выражение, позволяющее находить удельный заряд электрона
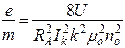 (5)
(5)
Формула (5) позволяет вычислить e/m, если при заданном U найдено такое значение магнитного поля (или, наоборот, при заданном В такое значение U), при котором электроны перестают попадать на анод. Это значит, что ток в цепи анода отсутствует. До сих пор предполагалось, что все электроны покидают анод с начальной скоростью равной нулю. В этом случае при I<Ik (В<Вк) все электроны без исключения попадали бы на анод, а при I>Ik (В>Вк) все возвращались бы на катод, не достигнув анода. 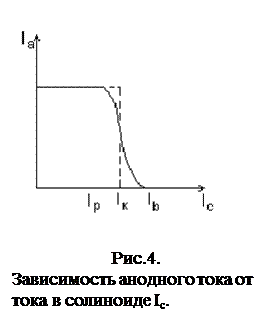 Анодный ток Ia с увеличением тока в соленоиде Ic, а, следовательно, и магнитного поля изменился бы при этом так, как это изображено на рис.4 пунктирной линией. На самом деле электроны, испускаемые нагретым катодом, обладают различными начальными скоростями. Критические условия достигаются поэтому для различных электронов при разных значениях тока соленоида, а, следовательно, и Во. Кроме того, несоосность катода и анода, отклонение магнитного поля от перпендикулярности к электрическому полю, приводят к сглаживанию кривой Ia=F(Ic), она приобретает вид сплошной линии на рис.4. За критическое значение тока Ik принимают некоторое среднее значение тока в соленоиде, лежащее в интервале
Анодный ток Ia с увеличением тока в соленоиде Ic, а, следовательно, и магнитного поля изменился бы при этом так, как это изображено на рис.4 пунктирной линией. На самом деле электроны, испускаемые нагретым катодом, обладают различными начальными скоростями. Критические условия достигаются поэтому для различных электронов при разных значениях тока соленоида, а, следовательно, и Во. Кроме того, несоосность катода и анода, отклонение магнитного поля от перпендикулярности к электрическому полю, приводят к сглаживанию кривой Ia=F(Ic), она приобретает вид сплошной линии на рис.4. За критическое значение тока Ik принимают некоторое среднее значение тока в соленоиде, лежащее в интервале 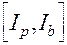 .
.
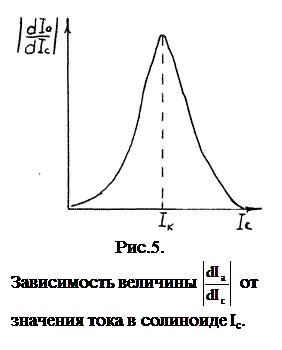 Для большей определенности удобно брать значение Ik, при котором производная
Для большей определенности удобно брать значение Ik, при котором производная 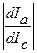 достигает максимума (см. рис.5).
достигает максимума (см. рис.5).
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. В качестве электронной лампы в данной работе используется двухэлектродная лампа 6Ц18П, схема питания которой приведена на рис.6. Работа начинается с изучения схем, представленных на рис.6 и рис.7.
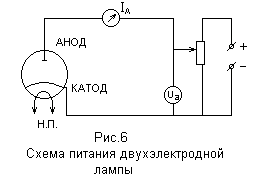
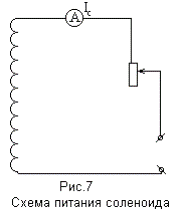
2. После проверки цепи преподавателем подают напряжение. Ручкой регулятора анодного напряжения устанавливают разность потенциалов между анодом и катодом около 10 В. Когда анодный ток примет стабильную величину, в таблицу 1 заносят первое показание Ia, соответствующее Ic=0. Затем плавно, через каждые 0,05 А, подают ток в обмотку соленоида, следя, чтобы напряжение на аноде поддерживалось постоянным в процессе измерений. Согласно табл.1 снимают показания анодного тока в функции от тока в соленоиде дважды: в прямой последовательности, когда ток в соленоиде возрастает, и обратно, через те же значения тока в соленоиде. Результаты усреднить.
Таблица 1
| Ток в | Анодный ток | Приращение | Приращение | |||
| соленоиде, Iс, А | Iа пр, А | Iа обр, А | Iа ср, А | анодного тока Iа, А | тока в соленоиде Iс, А | 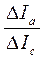 |
3. На основании данных табл.1 вычерчивают на миллиметровой бумаге две кривые. Первая дает зависимость Ia=F1(Ic). Вторая кривая – зависимость 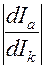 =
= 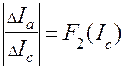 (см. рис.4 и 5). Максимальное значение
(см. рис.4 и 5). Максимальное значение 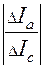 соответствует Ik соленоида.
соответствует Ik соленоида.
4. Для расчета искомой величины необходимо знать «параметры» катушки соленоида и анодного цилиндра. Эти данные указаны в табличке, прикрепленной на лабораторной установке. Их необходимо свести в табл.2, куда заносят также значения Ik и разность потенциалов U.
Таблица 2
| Разность потенциалов, U, В | Радиус анода, RА, м | Коэффициент К | Число витков, приходящихся на ед.длины соленоида, no, 1/м | Критич. ток в соленоиде, Iк, А |
По данным табл.2, согласно выражению (5), определяется удельный заряд электрона.
ТРЕБОВАНИЯ К ОТЧЕТУ
Отчет должен содержать следующее:
1. Принципиальную схему установки с небольшими пояснениями.
2. Результаты измерений в виде таблицы.
3. Графики зависимостей Ia=F1(Ic) и 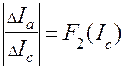 .
.
4. Расчет удельного заряда электрона.
5. Выводы по работе.
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
1. Что такое сила Лоренца? Как определяется ее величина и направление?
2. Покажите, что магнитное поле не совершает работы над зарядом.
3. Выведите расчетную формулу для определения e/m.
4. Почему анодный ток изменяется плавно с возрастанием тока в соленоиде?
5. При каких условиях анодный ток упадет до нуля скачком?
ЛИТЕРАТУРА
1. Методические указания к лабораторным работам по физике. Магнетизм (2 часть). Под ред.Агеева В.В. Тюмень.: ТИИ им.Ленинского комсомола. 1984.
2. Савельев И.В. Курс общей физики, т.2. – М.: Наука.1982. § 72, 73, 74.
3. Трофимова Т.И. Курс физики. – М.: Высш.шк., 1985. § 84, 116.
