Краткие теоретические сведенья. Идеальным называется газ, молекулы которого не взаимодействуют друг с другом на
Идеальным называется газ, молекулы которого не взаимодействуют друг с другом на расстоянии и имеют исчезающие малые собственные объемы. У реальных газов молекулы отталкиваются на малых расстояниях и притягиваются на больших. Но притяжение быстро уменьшается при увеличении расстояния, при атмосферном давлении и температуре около 300 К среднее расстояние между молекулами достаточно велико, чтобы взаимодействие считать пренебрежно малым для большинства газов. Соответственно для них выполняются законы идеального газа.
Состояние идеального газа характеризуется следующими параметрами состояния: массой газа m, объемом V,давлениемP,температуройT.Параметры состояния идеального газа взаимосвязаны уравнением Менделеева-Клапейрона:
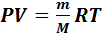, (7.1)
где R– универсальная газовая постоянная, R=8,31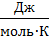 
; 
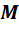- масса одного моля газа. Эта масса в граммах численно равна массе молекулы в атомах единицах массы, т.е. она пропорциональна массе молекулы. А значит, отношение массы моля к массе молекулы, равное числу молекул в одном моле, одинаково для всех веществ. Оно называется числом Авогадро и равно: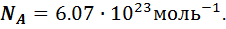 
Изменить состояние газа возможно путем передачи количества теплоты или совершением работы над газом. Количество теплоты, полученное газом, пропорционально изменению его температуры
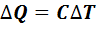,(7.2)
где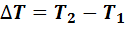 
- разность конечной и начальной температур; С-теплоемкость газа, равная количеству теплоты, необходимому для нагревания его на 1 К.
Для однородного вещества теплоемкость прямо пропорциональна его массе m:
C=cm, (7.3)
где с – удельная теплоемкость вещества, равная количеству теплоты, необходимому для нагревания единицы массы вещества на 1 К.
Теплоемкость одного моля вещества называется молярной теплоемкостью (обозначается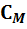 
):
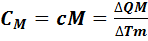. (7.4)
Количество теплоты, сообщенное газу, расходуется на изменение внутренней энергии газа и на совершение работы газом против внешних сил:
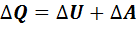,(7.5)
где 
- изменение внутренней энергии идеального газа; 
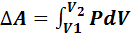– работа, выполненная газом. Уравнение (7.5) называется первым законом термодинамики.
При вычислении внутренней энергии идеального газа используется принцип равнораспределения энергии по степеням свободы молекулы. На каждую классическую степень свободы молекулы приходится средняя кинетическая энергия теплового движения, равная:
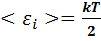(7.6)
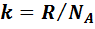- постоянная Больцмана, 
.
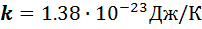Внутренняя энергия тела включает в себя кинетическую энергию теплового движения молекул, потенциальную энергию взаимодействия между всеми молекулами и внутримолекулярную энергию всех молекул. Последняя состоит из кинетической энергии движения частей молекулы друг относительно друга и потенциальной энергии их взаимодействия.
Внутренняя энергия идеального газа состоит только из кинетической энергии теплового движения молекул. Потенциальная энергия молекулярного взаимодействия пренебрежимо мала, части молекул при температурах порядка сотки кельвинов друг относительно друга не смещаются. Для получения внутренней энергии идеального газа достаточно среднюю энергию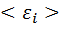 
умножить на число молекул газа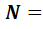 
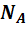
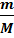и число степеней свободы молекул газа, т.е. число независимых координат, которыми можно задать положение молекулы в пространстве. Обозначим это число 
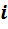. Тогда изменение внутренней энергии газа равно:
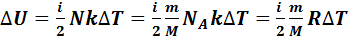. (7.7)
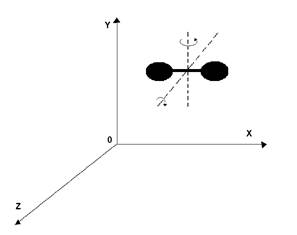
Двухатомные молекулы, из которых в основном состоит воздух (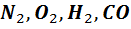 
)имеют 5 степеней свободы. Двухатомную модель можно представить в виде жесткого диполя. Центр масс этой системы имеет 3
Рисунок 7.1 степени свободы поступательного движения и 2 степени свободы вращательного движения. Момент инерции молекулы относительно оси ОХ равен нулю (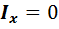 
), поэтому шестой степенью свободы пренебрегаем (рис. 7.1)
Если газ состоит из одноатомных молекул (инертные газы), то этим молекулам доступны только поступательные движения, они имеют три степени свободы (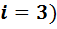 
.
Уравнение (7.5) можно представить в виде
+ 
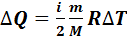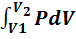(7.8)
В изохорном процессе объем газа остается неизменимым (V=const,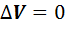 
), работа газом не совершается 
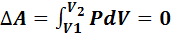.Следовательно, в изохорном процессе все тепло, переданное газу, идет на изменение его внутренней энергии:
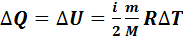(7.9)
Молярная теплоемкость в этом процессе называется изохорной, из формулы (7.4) следует, что она равна:
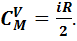(7.10)
Если процесс протекает при постоянном давлении (P=const), то он называется изобарным. В этом процессе происходит изменение внутренней энергии газа и выполняется работа газом против внешних сил:
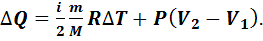(7.11)
Используя закон Менделеева-Клапейрона (7.1), вычисляем работу газа в изобарном процессе:
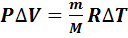.(7.12)
Первый закон термодинамики для изобарного процесса с учетом уравнений (7.7) и (7.12) записываем в виде
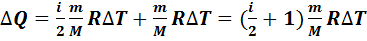(7.13)
Молекулярная теплоемкость в этом процессе также определяется формулой (7.4), она равна:
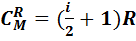.(7.14)
Сравнивая выражения (7.10) и (7.14), замечаем, что молярные теплоемкости зависят от числа степеней свободы молекулы. Отношение молярных теплоемкостей для воздуха определится:
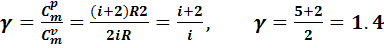.(7.15)
В практической части лабораторной работы предлагается определить отношение теплоемкостей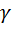 
экспериментально и сравнить его с теоретическим значением.