Пояснения к рабочей программе
Приступая к изучению физики, необходимо уяснить, что физика, наряду с другими естественными науками, изучает объективные свойства окружающего нас материального мира. Она исследует наиболее общие формы движения материи и их взаимные превращения. Движение есть форма существования материи. Физические понятия являются простейшими и в то же время основополагающими и всеобщими в естествознании (пространство, время, движение, масса, работа, энергия и др.).
Изучать основы классической механики надо исходя из представлений современной физики, в которой основные понятия классической механики не утратили своего значения, а получили дальнейшее развитие, обобщение и критическую оценку с точки зрения их применения. Следует помнить, что механика — это наука о простейших формах движения материальных тел и происходящих при этом взаимодействиях между телами. Движение всегда существует в пространстве и во времени. Диалектический материализм учит, что пространство и время являются основными формами существования материи. Предметом классической механики является движение макроскопических материальных тел, совершаемое со скоростями, малыми по сравнению со скоростью света в вакууме. Движение частиц со скоростями порядка скорости света рассматривается в теории относительности, а движение микрочастиц изучается в квантовой механике.
В контрольную работу №1 включены задачи, дающие возможность проверить знания студентов по ключевым вопросам классической механики и элементам специальной теории относительности. Решая задачи по кинематике, в которых необходимо использовать математический аппарат дифференциального и интегрального исчисления, студент должен научиться определять мгновенные скорость и ускорение по заданной зависимости координаты от времени и решать обратные задачи.
Задачи на динамику материальной точки и поступательного движения твердого тела охватывают такие вопросы, как закон движения центра масс механической системы, закон сохранения количества движения, работа силы и ее выражение через криволинейный интеграл, связь кинетической энергии механической системы с работой сил, приложенных к этой системе, закон сохранения механической энергии. Тщательного изучения и понимания требуют вопросы о поле как форме материи, осуществляющей взаимодействие между частицами вещества или телами, о потенциальной энергии механической системы.
В задачах на кинематику и динамику вращательного движения твердого тела главное внимание уделялось изучению соотношений между линейными и угловыми характеристиками, понятий момента силы, момента инерции тела, законов сохранения количества движения, момента количества движения и механической энергии.
В контрольную работу включены задачи по элементам специальной теории относительности, которые охватывают следующие вопросы: относительность одновременности, длин и промежутков времени, релятивистский закон сложения скоростей, зависимость релятивистской массы от скорости, соотношение между релятивистской массой и полной энергией. Решая эти задачи, студент должен усвоить, что законы классической механики имеют границу применимости и что они получаются как следствие теории относительности.
Изучая физические основы молекулярной физики и термодинамики, студенты должны уяснить, что существуют два качественно различных и взаимодополняющих метода исследования физических свойств макроскопических систем — статистический (молекулярно-кинетический) и термодинамический. Молекулярно-кинетический метод исследования лежит в основе молекулярной физики, термодинамический — в основе термодинамики. Молекулярно-кинетическая теория позволяет с единой точки зрения рассмотреть различные явления во всех состояниях вещества, вскрыть их физическую сущность и теоретическим путем вывести многочисленные закономерности, открытые экспериментально и имеющие большое практическое значение.
При изучения молекулярно-кинетической теории следует уяснить, что свойства огромной совокупности молекул отличны от свойств каждой отдельной молекулы и свойства макроскопической системы в конечном счете определяются свойствами частиц системы, особенностями их движения и средними значениями
кинетических характеристик частиц, т. е. их скоростей, энергий и т.д.
В отличие от молекулярно-кинетической теории, термодинамика не изучает конкретно молекулярные взаимодействия, происходящие с отдельными атомами или молекулами, а рассматривает взаимопревращения и связь различных видов энергии, теплоты и работы. Термодинамика базируется на опытных законах (началах), которые позволяют описывать физические явления, связанные с превращением энергии макроскопическим путем.
При изучении основ термодинамики студент должен четко усвоить такие понятия, как термодинамическая система, термодинамические параметры (параметры состояния), равновесное состояние, уравнение состояния, термодинамический процесс, внутренняя энергия, энтропия и т. д.
Задачи контрольной работы дают возможность проверить знания студентов по основным вопросам молекулярной физики и термодинамики.
В задачах на тему «Основы молекулярно-кинетической теории» внимание уделено таким вопросам программы, как уравнение Клапейрона — Менделеева, уравнение молекулярно-кинетической теории, средние кинетические энергии поступательного и вращательного движения молекул, средняя длина свободного пробега и среднее число соударений, явления переноса.
Задачи по теме «Основы термодинамики» охватывают такие важные соотношения и понятия, как первое начало термодинамики, внутренняя энергия, работа при различных изопроцессах и адиабатном процессе. Включены также задачи, которые позволяют изучить и понять такие вопросы, как второе начало термодинамики и энтропия идеального газа, являющаяся в отличие от количества теплоты функцией состояния.
Задачи в контрольной работе расположены приблизительно в том порядке, в каком соответствующие вопросы рассматриваются в рабочей программе.
ОСНОВНЫЕ ФОРМУЛЫ
Скорость мгновенная ν 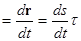 ,
,
где r – радиус-вектор материальной
точки,
t – время,
s – расстояние вдоль траектории
движения,
τ – единичный вектор, касательный
к траектории.
Ускорение:
мгновенное 
а 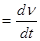 ;
;
тангенциальное
аτ 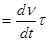 ;
;
нормальное
аn  n;
n;
полное
а= аτ+аn, 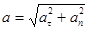 ,
,
где R – радиус кривизны траектории,
n – единичный вектор главной
нормали.
Скорость угловая
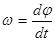 ,
,
где φ – угловое перемещение.
Ускорение угловое
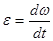 .
.
Связь между линейными и угловыми
величинами s = φR, υ = ωR,
aτ = εR, an = ω2R.
