Возмущения, обусловленные отличием гравитационного поля Земли от центрального
В одном, весьма важном для практики случае, уравнения возмущенного движения могут быть упрощены, а именно, когда возмущающие силы потенциальны.
Функция V, являющаяся функцией координат точки, называется силовым потенциалом, или силовой функцией, если сила 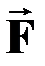
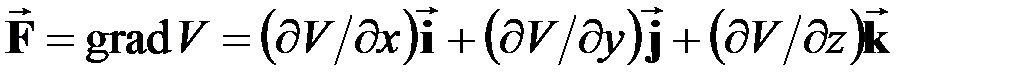 . (1.27)
. (1.27)
Функция П = –V называется потенциальной энергией точки.
Силовой потенциал Vсф, создаваемый силой тяготения сферической Земли, соответствующей невозмущенному движению, определяется по формуле:
Vсф. = m/r. (1.28)
Для земного эллипсоида потенциал можно представить в виде ряда:
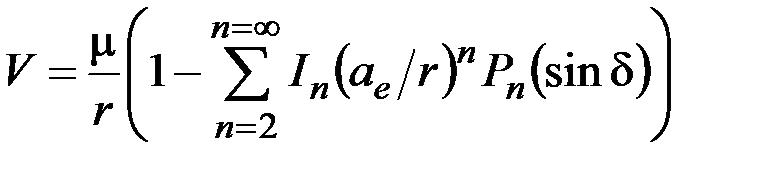 , (1.29)
, (1.29)
где In – постоянные, характеризующие потенциал; ae – экваториальный радиус Земли; r – геоцентрический радиус-вектор ИСЗ; Pn (sin d) – полиномы Лежандра по sin d порядка n.
При этом геоцентрическое склонение d ИСЗ равно геоцентрической широте F, которая связана с геодезической широтой B формулой:
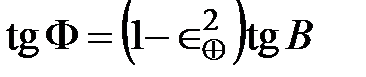 , (1.30)
, (1.30)
где 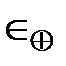 – эксцентриситет общего земного эллипсоида.
– эксцентриситет общего земного эллипсоида.
Коэффициенты I2, ... , In, входящие в выражение (1.30), называются коэффициентами зональных гармоник, а сами члены разложения (1.30) – зональными гармониками.
Определяющее значение имеет коэффициент I2 при второй зональной гармонике, которая задает динамическое сжатие Земли. Остальные коэффициенты значительно меньше.
По данным Смитсонианской Астрофизической обсерватории (САО) значения параметров:
I2 = 1082,639·10–6;
I3 = –2,565·10–6;
I4 = –1,608·10–6;
I5 = –0,174·10–6.
Параметры I4, I6, ... , I2n характеризуют симметричные относительно экватора вариации гравитационного поля геоида. Параметры с нечетными (I3, I5, ... I2n) индексами характеризуют асимметричные относительно экватора вариации земного поля.
Разность потенциалов:
R = V – Vсф. (1.31)
называют возмущающим потенциалом или пертурбационной функцией, которая вызывает изменения кеплерова эллипса во времени.
Все возмущения орбит разделяют соответственно их периодам на три группы: вековые, долгопериодические и короткопериодические.
Долгопериодические возмущения имеют периоды от 100 до 200 суток. Часть их вызваны сжатием Земли и связаны с вековыми возмущениями аргумента перицентра w, поскольку тригонометрические функции w изменяются с периодом 2p. На долгопериодические возмущения накладываются короткопериодические, которые определяются тригонометрическими функциями линейных комбинаций М и q или w.
Параметр орбиты р за один оборот спутника вокруг Земли испытывает два полных колебания с амплитудой
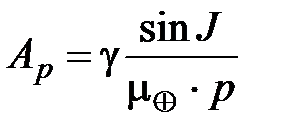 , (1.32)
, (1.32)
где g = 2,634·1010 км5·с–2 — постоянная поля тяготения земного эллипсоида.
Наклонение орбиты J также совершает периодические колебания с максимальной амплитудой
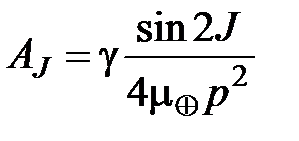 . (1.33)
. (1.33)
