Потери при двух временах релаксации
Как было показано, теория дипольных потерь правильно описывает частотные и температурные зависимости ε', ε" и tg δ, если после выключения электрического поля поляризация уменьшается по экспоненциальному закону. Это имеет место, если у всех молекул одно и то же среднее время оседлой жизни. Если же имеются два вида молекул с различными временами оседлой жизни и различными временами релаксации, например, со временами релаксации поляризации τ1 и τ2, причем τ1 > τ2, то в частотном ходе tgδ будут наблюдаться два максимума.
Первый максимум будет лежать при относительно низкой частоте ω1, которая определяется из условия, подобного ,
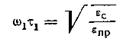 .
.
Второй максимум располагается при более высокой частоте ω2, вычисленной по формуле
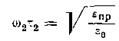 .
.
где εc и ε0 — статическая и безынерционная оптическая диэлектрические проницаемости;
εпр — диэлектрическая проницаемость в интервале частот ω1 — ω2;
εс>εпр>ε0
Если частоты ω1 и ω2 значительно различаются и максимумы разделены, то величина tg δ в максимумах при частотах ω1 и ω2 равняется:
при частоте ω1
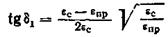 .
.
при частоте ω2
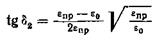 .
.
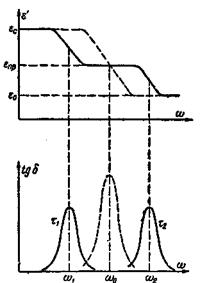 Рис. 7‑5 Зависимость ε' и tg δ от частоты для двух случаев: одного времени релаксации (пунктирные кривые); двух времен релаксации τ1 и τ2 (сплошные кривые). Рис. 7‑5 Зависимость ε' и tg δ от частоты для двух случаев: одного времени релаксации (пунктирные кривые); двух времен релаксации τ1 и τ2 (сплошные кривые). |
Сопоставляя , и , видим, что каждый из двух разделенных максимумов tg δ меньше максимальной величины tgδ для случая, когда имеется только один вид молекул или когда τ1 = τ2 и ω1 = ω2. Если τ1 = τ2, то максимумы, накладываясь, усиливают друг друга, приводя к большей величине результирующего максимума.
На Рис. 7‑5 показаны частотные зависимости ε' и tg δ:
1) для случая, когда τ1 и τ2, ω1 и ω2 существенно различаются, ε' и tgδ представлены сплошными кривыми,
2) для случая, когда τ1 = τ2, и tg δ изображены пунктирными кривыми. Зависимости с двумя или несколькими максимумами потерь наблюдаются для многих диэлектриков, в которых имеются разные молекулы. Например, на Рис. 7‑6 приведена зависимость tg δ от температуры для конденсаторной бумаги, пропитанной масляноканифольным компаундом.
Если времена релаксации τ1 и τ2 и, следовательно, частоты ω1 и ω2 близки друг к другу, то получается более широкий и высокий максимум, чем в том случае, если частоты ω1 и ω2 были равны.
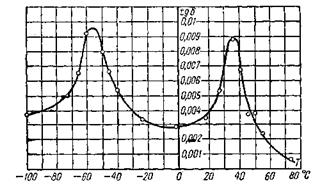 Рис. 7‑6. Зависимость tg δ от температуры для конденсаторной бумаги, пропитанной компаундом (80% канифоли плюс 20% трансформаторного масла) Рис. 7‑6. Зависимость tg δ от температуры для конденсаторной бумаги, пропитанной компаундом (80% канифоли плюс 20% трансформаторного масла) |
Набор времен релаксации τ, лежащих близко друг к другу, дает низкий размытый максимум в частотном ходе tg δ, что ясно из Рис. 7‑7. Широкий максимум можно представить как результат наложения близко лежащих максимумов молекул с различными временами релаксации.
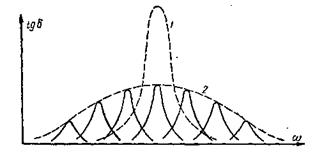 Рис. 7‑7. Зависимость tg δ от частоты для диэлектрика / — с одним временем релаксации; 2 — с набором времен релаксации Рис. 7‑7. Зависимость tg δ от частоты для диэлектрика / — с одним временем релаксации; 2 — с набором времен релаксации |
Измерения частотных зависимостей tg δ многих диэлектриков дают для tg δ меньшее значение в максимуме, чем формула , и более широкий максимум, чем вычисленный по формуле . Это расхождение экспериментальных данных с выводами теории объясняется наличием набора времен релаксации. Даже одинаковые молекулы в диэлектрике с одним видом молекул могут иметь различные времена релаксации. Поэтому формулы следует уточнить, учтя, что может иметься набор времен релаксации. Надо отметить, что для некоторых диэлектриков эти формулы дают значения ε', ε" и tgδ, хорошо совпадающие с измеренными.
