Тогда окончательно получаем

IR_{1, 2} = U_{1, 2} + e. (4.10)

Выражение (4.10) является законом Ома в интегральной форме для цепи содержащей Э.Д.С. Если на данном участке источник тока отсутствует (ε = 0), то (4.10) переходит в обычный закон Ома (4.2).

Рассмотрим пример источника тока с Э.Д.С. e и внутренним сопротивлением r, замкнутого на внешнюю цепь (потребителя) с сопротивлением R. В цепь включены амперметр А, измеряющий ток I и вольтметр V, измеряющий напряжение U у потребителя. В качестве потребителя используем реостат R переменного сопротивления.

Полное сопротивление всей цепи R_полн = r + R и закон Ома для всей цепи примет вид

I(R + r) = e , (4.11)

или

.

Поскольку на участке внешней цепи Э.Д.С. отсутствует, то

U = IR = .

Формула дает зависимость напряжения от сопротивления нагрузки.

Если участок цепи не содержит Э.Д.С., а к нему приложена разность потенциалов U_{1, 2} и идет ток I, то за некоторый промежуток времени t через участок пройдет заряд q = It, при этом силы электрического поля совершат работу по переносу заряда от точки с более высоким к точке с более низким потенциалом.

A = (j₁ - j₂)q = U_{1, 2}I t. (4.12)

В соответствии с законом Ома эту работу можно выразить через сопротивление участка R:

A = I²R t = . (4.13)

Если на участке цепи находится источники тока, то при переносе заряда q работу совершают силы электрического поля и сторонние силы:

A = (U_{1, 2} + e)I t = I²R_{1, 2}t , (4.14)

или в случае замкнутой цепи из двух слагаемых A = U_{1, 2}I t + e I t первое обращаются в нуль, так как полное падение потенциала U_{1, 2} во всей цепи равно нулю. Поэтому

A = e I t = I²R_полн t . (4.15)

Работа, совершаемая за единицу времени: , есть выделяемая мощность. Для участка цепи

P = IU_{1, 2} + Ie.. (4.16)

Для всей цепи: P_полн = Ie.. (4.17)

Мощность, выделяемая во внешней цепи

P_вн = I U = I² R = . (4.18)

Для поддержания в цепи постоянного тока необходимо совершать работу А. Энергия электрического тока в проводнике непрерывно расходуется и переходит в другие формы энергии. Действительно, проводник, по которому течет ток, нагревается и в нем выделяется некоторое количество тепла Q. Если других потерь нет, то по закону сохранения энергии

A = Q = I U t = I² R t = , (4.19)

Эти соотношения выражают закон Джоуля - Ленца.

Если в цепь включено очень малое сопротивление DR, то падение напряжения ничтожно, и ток в цепи определяется лишь сопротивлением остальной цепи и приборов большого сопротивления.

Тогда для расчета количества тепла, выделяемого на DR, следует использовать формулу: DQ = I²DR t.

В этом случае тепловая мощность DQ/t определяется только током в цепи I. Выполняя такое сопротивление из тонкой проволочки длины Dl и поперечного сечения S, мы видим, что

,

или

т.е. количество тепла, выделяющегося на единицу длины проволочки, тем больше, чем меньше её сечение.

В классической электронной теории металлов предполагается, что при соударения с ионами электроны полностью теряют скорость упорядоченного движения. Уравнение движения электрона в процессе свободного пробега имеет вид:

(4.20)

где E - напряженность электрического поля в проводнике. В процессе свободного пробега электроны движутся равноускоренно. Поэтому средняя скорость их упорядоченного движения где <J_max> - средняя скорость электрона, приобретаемая под действием электрического поля на длине свободного пробега. Интегрируя это уравнение движения электрона по времени от 0 до < t >, получаем

. (4.21)

Электроны одновременно участвуют также в тепловом движении. Пренебрегая статическим распределением электронов проводимости по скоростям их теплового движения, будем считать, что модули скоростей всех электронов в этом движении одинаковы и равны <U>. Тогда, учитывая что <J > << <U>, можно определить среднее время свободного пробега электронов по формуле:

<t> = <l>/<U>, (4.22)

где <l> - средняя длина свободного пробега электронов. Подставим (4.22) в (4.21) для < J >:

< J> = e<l>E / (2m<U>). (4.23)

Из формулы для плотности тока I :

, (4.24)

где n₀ - концентрация электронов проводимости , e - заряд электрона, <J > - средняя скорость дрейфа электронов. Из формулы для <J > (4.23), следует, что плотность тока проводимости в металле

I = n₀e²<l>E / (2m<U>),

Величину g = n₀e²<l>/ (2m<U>) , (4.25)

называют удельной электрической проводимостью, а обратную ей величину - удельным электрическим сопротивлением.

В единице объема проводника имеется n₀ электронов проводимости, каждый из которых испытывает ежесекундно в среднем <U>/<l> столкновений с ионами металла. Следовательно, энергия тока, равная

<DW_э> = 0.5 m <J_max>² ,

преобразующаяся во внутреннюю энергию в единице объема проводника за 1с, равна:

. (4.26)

Величину w называют объемной плотностью тепловой мощности тока. Заменяя <J_max> по формуле (4.21), где <t> = <l>/<U>, получаем

w = n₀e²<l>E² / (2m<U>)

или

w = gE² (4.27)

Это уравнение выражает закон Джоуля - Ленца для плотности тепловой мощности тока. Его часто называют законом Джоуля - Ленца в дифференциальной форме.

Закон Джоуля ленца можно также переписать в форме

w = IE = I²/ g = r I². (4.28)

Рассмотрим участок цепи, содержащий источник тока с ЭДС e, внутренним сопротивлением r, замкнуты на внешнюю цепь сопротивлением R. В пределе, когда R®0, источник тока замкнут накоротко, говорят о режиме короткого замыкания. В этом случае ток максимален:

I = e /r = I_max,

Тогда, в соответствии с законом Джоуля - Ленца, количество теплоты, выделяемое в проводнике Q будет максимальным, что приводит к возгоранию и прочих негативным последствиям. Напряжение при этом во внешней цепи будет равно нулю. В противоположном предельном случае, R® ¥, цепь разомкнута, и ток отсутствует, а напряжение максимально и равно ЭДС источника. Такой режим называется холостым ходом.

Из закона Ома для полной цепи

e = I(R+r) = IR + Ir = U+Ir

или

U = e - Ir. (4.29)

Полученная зависимость U(I) называется нагрузочной характеристикой источника тока. Построив график зависимости U(I) можно найти e источника тока и его внутреннее сопротивление, экстраполировав его.

e = U_I=0 ; r = e / I_U=0 . (4.30)

Полную мощность, развиваемую источником ЭДС модно записать в виде:

N = e I. (4.31)

Подставив в (4.31) закон Ома для полной цепи I = e /(R+r) получим полную мощность, выделяемую во всей цепи:

N = e²/(R+r). (4.32)

В нагрузке выделяется только часть этой мощности

N_R = UI = I²R = (4.33)

Эту мощность называют полезной. Максимальное значение полезной мощности достигается при условии согласованной нагрузки, т.е. R = r. Это можно доказать, исследовав функцию в выражении (4.33) на экстремум.

Отношение полезной и полной мощности развиваемой ЭДС в цепи, называется коэффициентом полезного действия источника тока:

h = N_R / N. (4.34)

Используя выражения (4.32) и (4.33) можно получить формулу:

h = R / (R+r), (4.35)

из которой видно, что КПД источника тока зависит от нагрузочного сопротивления R. При условии R = r КПД равен 50%.

Схема

В данной установке используются источник постоянного тока (0 ¸ 7В), два мультиметра, один в режиме вольтметра, другой в режиме амперметра; нагрузкой является магазин сопротивлений. Для того, чтобы исключить возможность получения короткого замыкания подключают дополнительное сопротивление R_Д, выбирая одно из сопротивлений моста.

Порядок выполнения работы

1. Собираем схему по рис.4. 3.

2. С помощью вольтметра устанавливают напряжение порядка 3¸5В (постоянный ток), на источнике питания 0¸7В.

3. Устанавливают на магазине сопротивление, порядка 10 кОм (используя только один тумблер переключения на магазине, около которого стоит множитель х10³).

4. Понижая сопротивление нагрузки на 1кОм, замеряют значения тока и напряжения на ней.

5. Результаты измерений представляют в виде таблицы, в которой должно быть не менее 11 значений.

Таблица

№ п/п	U B	I A	R Ом	NR Вт	N Вт	h %

6. По данным 2 и 3 колонок таблицы построить график нагрузочной характеристики источника тока U = U(I).

7. Экстраполируя нагрузочную линию до пересечения с осями I и U находим по формуле (4.30) e и r источника.

8. По закону Ома вычислить сопротивление нагрузки.

9. По формуле (4.33) рассчитать мощность N_R, выделяемую на нагрузке и результаты занести в таблицу.

10. Построить график зависимости мощности в нагрузке N_R от сопротивления нагрузки N_R= N_R(R).

11. По графику проверить условие согласованной нагрузки.

12. По формуле (4.31) рассчитать полную мощность N, а по формуле (4.34) - КПД источника тока и результаты занести в таблицу.

13. Построить график к зависимости h=h(R).

14. По одному из полученных результатов определить погрешность полученных значений методом косвенных измерений.

Контрольные вопросы

1. Основные характеристики источника и их нахождение из нагрузочной прямой.

2. Вывод законов Ома и Джоуля - Ленца (дифференциальная и интегральная форма).

3. Проводимость, удельная проводимость, плотность тока.

4. Холостой ход и режим короткого замыкания.

5. Полная и полезная мощность, КПД источника тока. Как зависят от R и их значения при согласованной нагрузке.

Литература

1. Зисман Г.А., Тодес О.М. Курс общей физики, М.: Наука, 1974. II том.

2. Калашников С.Г. Электричество, М.: Наука, 1985. Гл. 6.

3. Яворский Б. М., Детлаф А.А. Курс физики, М.: Высшая школа, 1983. II том.

4. Сорокин А.Ф., Сурков М.И., Кушкин С.А. Руководство к лабораторным работам по физике. Астрахань 1997.

Лабораторная работа № 5.

Зависимость сопротивление материалов от температуры.

Цель работы: изучить зависимость сопротивления материалов от температуры.

Оборудование: источник питания 8,4 В, мультиметр М2, соединительные провода.

Краткая теория

Электрический ток в металлах – это направленное движение электронов. Такой характер их движения обусловлен наличием электрического поля в проводнике. В случае слабых полей в металлах выполняется закон Ома:

. (5.1)

Причинами, вызывающими появление электрического сопротивления R в металлах, являются физические дефекты кристаллической решетки, а так же тепловое движение ионов металла, амплитуда колебаний которых увеличивается с ростом температуры. При комнатных температурах и выше основной причиной роста сопротивления металлов является увеличение рассеяния электронов проводимости на тепловых колебаниях кристаллической решетки при увеличении температуры металлов. Как следует из теории проводимости металлов, в указанном диапазоне температур, зависимость R от t^оС должна быть близка к линейной.

, (5.2)

где R₀ – сопротивление при 0⁰С,

α – температурный коэффициент сопротивления (т.к.с.).

Для большинства металлов в интервале температур 0÷100⁰С α изменяется в пределах (3,3÷6,2)^.10^-3 град^-1.

В некоторых металлах и сплавах обнаруживается явление сверхпроводимости, заключающееся в том, что ниже некоторой критической температуры (Т_с - температура перехода в сверхпроводящее состояние) сопротивление этих веществ, становится исчезающее малым. Температурная зависимость удельного сопротивления сверхпроводников обнаруживает конечную ширину АВ (рис. 5.1) переходной области возникновения сверхпроводимости, зависящую от наличия примесей и внутренних напряжений. Температуры Т_с для чистых металлов лежат в пределах от 0,35К (гафний) до 8К (ниобий); у сплавов – от 0,155К (Bi Pt) до 18Κ (Νb Sn₃). Температуры Т_с обратно пропорциональны квадратным корням из атомных весов изотопов одного и того же сверхпроводящего металла (изотопический эффект).

Полупроводники – большой класс веществ, удельное сопротивление которых изменяется в широких пределах (при комнатных температурах ρ ≈ 10^-5÷10^-7Ом ^. м) и в очень сильной степени уменьшается с увеличением температуры (по экспоненциальному закону). В периодической системе Д.И. Менделеева полупроводники образуют группу элементов, изображённую на (рис.5.2). В полупроводниках и диэлектриках для получения электропроводности требуется перевести валентные электроны из связанного в свободное состояние. Для этого валентному электрону нужно сообщить дополнительную кинетическую энергию, равную или большую энергии связи. Указанный процесс можно получить облучением (внутренний фотоэффект) или нагреванием. Энергия, которую нужно сообщить валентному электрону, чтобы разорвать его связь с данным атомом, называется энергией активации электрона. Полупроводники отличаются от диэлектриков малой величиной энергии связи валентных электронов, т.е. малыми энергиями активации, в полупроводниках обычно не превосходит 1эВ (1 эВ = 1,6^.10^-19 Дж), в то время как в диэлектриках она достигает 10 эВ. Малость энергии связи валентных электронов в полупроводниках делает их эмпирические свойства чувствительными к внешним воздействиям, что привело к широкому использованию полупроводников в различных областях техники, и особенно в электронике. Современная теория свойств полупроводников называется зонной теорией.

Как показывает зонная теория, температурная зависимость сопротивления проводников описывается формулой:

, (5.3)

где А – константа, зависящая от размеров полупроводника и концентрации валентных электронов;

k = 1,38^.10^-23 Дж/К = 0,87^.10^-4 эВ/К – постоянная Больцмана;

Т- температура по шкале Кельвина;

W - энергия активации в электрон – вольтах (эВ).

Из зависимости R(T), используя формулу (5.3), можно определить энергию активации. Для этого прологарифмируем формулу (5.3):

. (5.4)

Как видно из (5.4) зависимость 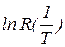должна быть линейной, с тангенсом угла наклона:

. (5.5)

Таким образом, построив график 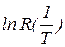, можно определить энергию активации.