Энтропия, ее статистическое толкование. Порядок и беспорядок в природе. Второе начало термодинамики
Энтропия идеального газа(термодинамическое толкование).
Для обратимого цикла Карно: 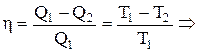 можно получить:
можно получить:
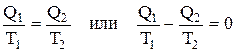 . Но Q2<0 , т.к. отдается системой => алгебраическая сумма:
. Но Q2<0 , т.к. отдается системой => алгебраическая сумма:
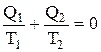 . (7.6.1.)
. (7.6.1.)
Отношение 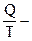 называется приведенным количеством теплоты.
называется приведенным количеством теплоты.
Из (7.6.1.) следует утверждение:
для цикла Карно алгебраическая сумма приведенных количеств теплоты равна нулю.
Анализ показывает: что для любогообратимого кругового процесса сумма приведенных количеств теплоты равна 0 . => (7.6.1) в общем виде запишется как интеграл:
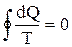 , (7.6.2.)
, (7.6.2.)
где 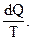 - приведенное количество теплоты на бесконечно малом участке процесса.
- приведенное количество теплоты на бесконечно малом участке процесса.
Величину 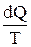 обозначают dS т.е.
обозначают dS т.е. 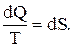 (7.6.3.)
(7.6.3.)
Функция состояния, дифференциалом которой является приведенное количество теплоты 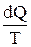 , называется энтропией и обозначается S.
, называется энтропией и обозначается S.
Рассматривая также необратимые процессы, было полученонеравенство Клаузиуса:
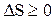 ,
,
Т.е. энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов).
Если система совершает равновесный переход из состояния 1 в состояние 2, то согласно (7.6.3.), изменение энтропии
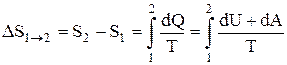 . (7.6.4.)
. (7.6.4.)
Данная формула определяет энтропию лишь с точностью до аддитивной постоянной. Физический смысл имеет не сама энтропия, а разность энтропий, при этом изменение энтропии не зависит от вида процесса перехода 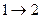 .
.
При изобарном процессе:
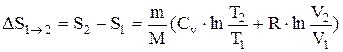 . (7.6.5.)
. (7.6.5.)
При изотермическом процессе ( 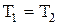 ):
): 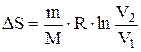 . (7.6.6)
. (7.6.6)
При изохорном процессе ( 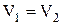 ):
): 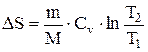 . (7.6.7)
. (7.6.7)
Адиабатический процесс протекает при постоянной энтропии, т.е. 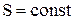 , т.к.
, т.к. 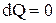 , то и
, то и 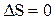
Энтропия облает свойством аддитивности: энтропия системы равна сумме энтропий тел, входящих в систему. Данным свойством обладают также внутренняя энергия, масса.
Более глубокий смысл энтропии вскрывается в статистической физике: энтропия связывается с термодинамической вероятностью состояния системы.
Термодинамическая вероятность состояния системы W- это число способов, которыми может быть реализовано данное состояние макроскопической системы, или число микросостояний, осуществляющих данное макросостояние (по определению, 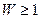 ).
).
Энтропия системы и термодинамическая вероятность связаны между собой следующим образом (формула Больцмана):
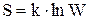 , (7.6.8)
, (7.6.8)
где k – постоянная Больцмана.
Таким образом, энтропия определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние. Следовательно, энтропия может рассматриваться как мера вероятности состояния термодинамической системы. Формула (7.6.8) позволяет дать энтропии следующее статистическое толкование:энтропия является мерой неупорядоченности системы.
Чем больше число микросостояний, реализующих данное макросостояние, тем больше энтропия. В состоянии равновесия – наиболее вероятного состояния системы - число микросостояний максимально, при этом максимальна и энтропия.
Так как реальные процессы необратимы, то можно утверждать, что все процессы в замкнутой системе ведут к увеличению ее энтропии –принцип возрастания энтропии.При статистическом толковании энтропии это означает, что процессы в замкнутой системе идут в направлении увеличения числа микросостояний, иными словами, от менее вероятных состояний к более вероятным, до тех пор, пока вероятность состояния не станет максимальной.
Второе начало термодинамики или закон возрастания энтропии замкнутой системы при необратимых процессах: любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает.
